Unsymmetrical Fault Calculations

425

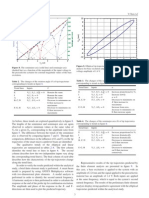
The current in any phase is equal to the vector sum of positive, negative and zero phase sequence currents in that *phase as shown in Fig. 18.4.

I R = I R1 + I R 2 + I R 0 IY

= I Y1 + I Y 2 + I Y 0

I B = I B1 + I B 2 + I B0

The following points may be noted : (i) The positive phase sequence currents ( I R1 , I Y1 and I B1 ), negative phase sequence currents ( I R2 , I Y 2 and I B2 ) and zero phase sequence currents ( I R0 , IY 0 and I B0 ) separately form balanced system of currents. Hence, they are called symmetrical components of the unbalanced system. (ii) The symmetrical component theory applies equally to 3-phase currents and voltages both phase and line values. (iii) The symmetrical components do not have separate existence. They are only mathematical components of unbalanced currents (or voltages) which actually flow in the system. (iv) In a balanced 3-phase system, negative and zero phase sequence currents are zero. This is demonstrated in example 18.7.

18.3 Operator a
As the symmetrical component theory involves the concept of 120 displacement in the positive sequence set and negative sequence set, therefore, it is desirable to evolve some operator which should cause 120 rotation. For this purpose, operator a (symbols h or are sometimes used instead of a) is used. It is defined as under : The **operator a is one, which when multiplied to a vector rotates the vector through 120 in the anticlockwise direction. Consider a vector I represented by OA as shown in Fig. 18.5. If this vector is multiplied by operator a, the vector is rotated through 120 in the anticlockwise direction and assumes the position OB. a I = I 120 = I (cos 120 + j sin 120)
* ** Star connected system being considered in Fig. 18.4. Just as the operator j rotates a vector through 90 in the anticlockwise direction.