Professional Documents
Culture Documents
Trig Review
Trig Review
Uploaded by
asdfjklasdfjkl123Copyright:
Available Formats
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5822)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1093)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (852)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (898)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (349)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (403)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Electrical Cheat SheetDocument10 pagesElectrical Cheat SheetM J Rhoades67% (6)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Six Trigonometric RatiosDocument4 pagesSix Trigonometric RatiosJomar Gregorio100% (10)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Formulas For EE 201Document3 pagesFormulas For EE 201berickson_14No ratings yet
- Logic Gates-Boolean Algebra-Karnaugh MapDocument1 pageLogic Gates-Boolean Algebra-Karnaugh Mapberickson_14No ratings yet
- EE-2110 - Formula SheetDocument2 pagesEE-2110 - Formula Sheetberickson_14No ratings yet
- Trig Cheat SheetDocument4 pagesTrig Cheat Sheetapi-284574585No ratings yet
- θ α - alpha β - beta γ - gamma: theta Obtuse Angle Between 90 & 180Document8 pagesθ α - alpha β - beta γ - gamma: theta Obtuse Angle Between 90 & 180charmaine padorNo ratings yet
- The Trigonometric Functions We Will Be Looking At: Sine Cosine TangentDocument23 pagesThe Trigonometric Functions We Will Be Looking At: Sine Cosine TangentGenne kayeNo ratings yet
- Induction ProblemsDocument2 pagesInduction ProblemsMaged SamuelNo ratings yet
- Ba136 PDFDocument293 pagesBa136 PDFZen AlkaffNo ratings yet
- Practice Problem No. 2Document8 pagesPractice Problem No. 2AaRichard ManaloNo ratings yet
- Maths Class 11 HOTS Important Question 22Document8 pagesMaths Class 11 HOTS Important Question 22srinidhiNo ratings yet
- James Ruse 2005 3U TrialDocument7 pagesJames Ruse 2005 3U TrialEmilyWongNo ratings yet
- Trig 1 NotesDocument7 pagesTrig 1 NotesMrs. HedrickNo ratings yet
- Pre - Calculus - Module 7Document15 pagesPre - Calculus - Module 7Sharlene Mae BuitizonNo ratings yet
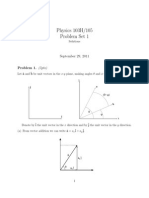
- Phy 105 Problem Set 1 Solutions 2012Document9 pagesPhy 105 Problem Set 1 Solutions 2012pbrowning9416No ratings yet
- The Expert TA - 3aaDocument6 pagesThe Expert TA - 3aaMuzamil ShahNo ratings yet
- MAT 461, Prof. Swift The Fourier Cosine Series of sin (πx/L)Document2 pagesMAT 461, Prof. Swift The Fourier Cosine Series of sin (πx/L)NITIN KUMARNo ratings yet
- Vector Algebra Tutorial QuestionsDocument5 pagesVector Algebra Tutorial QuestionsmubbaahNo ratings yet
- SurveyingDocument11 pagesSurveyingRobin TubleNo ratings yet
- Final Exam Review CummulativeDocument33 pagesFinal Exam Review CummulativeAj Koenig0% (1)
- Calculus Reference and NotesDocument3 pagesCalculus Reference and NotesLexy TeoNo ratings yet
- Fourier Integrals and Fourier TransformsDocument7 pagesFourier Integrals and Fourier TransformsVraj MehtaNo ratings yet
- Testlab Software Reference Manual - Functions and FormulasDocument12 pagesTestlab Software Reference Manual - Functions and Formulasmuhammad irfanNo ratings yet
- Digital Compensator Design For LLC Resonant ConverterDocument28 pagesDigital Compensator Design For LLC Resonant ConverterVũ Hùng TrángNo ratings yet
- c3 TrigonometryDocument13 pagesc3 Trigonometryazmat18No ratings yet
- Lecture 05 Complex Number Part 01Document54 pagesLecture 05 Complex Number Part 01Logix FicsarioNo ratings yet
- Self-Assessment: 8 Circular Measure and Trigonometric FunctionsDocument2 pagesSelf-Assessment: 8 Circular Measure and Trigonometric FunctionsboostoberoiNo ratings yet
- Sheets Matlab 2Document1 pageSheets Matlab 2Mahmoud EldabahNo ratings yet
- PDFDocument207 pagesPDFPaulmoNo ratings yet
- sin α cos α 1 + = a b a + bDocument13 pagessin α cos α 1 + = a b a + bvedfhgjsljgNo ratings yet
- Bk5 Sol C14 EDocument36 pagesBk5 Sol C14 EMa Ka YiNo ratings yet
- Trigonometry Exact Values: IGCSEDocument26 pagesTrigonometry Exact Values: IGCSEZoon AANo ratings yet
- The Sine and Cosine Rule Worksheets Questions and Revision MMEDocument1 pageThe Sine and Cosine Rule Worksheets Questions and Revision MMEmohitNo ratings yet
- Higher 2 Mathematics: Paper 1Document6 pagesHigher 2 Mathematics: Paper 1Seng SoonNo ratings yet
Trig Review
Trig Review
Uploaded by
asdfjklasdfjkl123Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Trig Review
Trig Review
Uploaded by
asdfjklasdfjkl123Copyright:
Available Formats
Trigonometry Review
Workshop 1
Definitions: Let P(x,y) be any point (not the origin) on the terminal side of an angle with measure and let r be the distance from the origin to P. Then the six trig functions are defined as follows:
r x sin = cos = opposite hypotenuse adjacent hypotenuse opposite adjacent = = y r x r = sin cos
csc = sec =
r 1 = y sin r 1 = x cos cos x 1 = = y tan sin
= y x
tan =
cot =
Measuring Angles There are 360o in a circle and 2 radians. They are marked off on the circle below:
2/3, 120 3/4, 135 5/6, 150
/2, 90 /3, 60
/4, 45
30, /6
, 180
2, 0
7/6, 210 5/4, 225 4/3, 240
11/6, 330 7/4, 315 3/2, 270 5/3, 300
To convert from degrees to radians (and vice versa) we use the fact that 180o = radians.
Example: Convert 36o to radians. Using the ratio 180o we find that 36 o = 36o 2 = 10 = 5 radians 180o
Reference Angles The angle formed by the terminal side of the angle and the x-axis is called the reference angle. The six trig functions of any angle are determined by it's reference angle and the quadrant it is in.
R = 180o -
R = 180
R = 360o -
The signs of the three major trig functions are determined by the quadrant as follows: Quadrant I: All are positive Quadrant II: S ine is positive Quadrant III: Tangent is positive Quadrant IV: Cosine is positive This can be remembered by the pneumonic device All Students Take Calculus. Since 1 csc = , sine and cosecant always have the same sign. The is true of Cosine, Secant, and Tangent, sin Cotangent as well. Special Triangles: We can use the ratios of some common triangles, along with the definitions of the trig. functions to determine the trig functions of some special angles. Using the two triangles below we see that:
2
45
45
1
30
60
1 2 sin 45o = = 2 2 cos 45o = tan 45o = 1 2 1 =1 1 = 2 2
1 sin 30o = 2 cos 30o = tan 30o = 3 2 1 3 = 3 3
and similarly for 60o. This is left as an exercise. Practice Exercises #1 1. Find the six trig functions of 60o. 2. Find the six trig functions for each of the following angles as shown: a. b.
y 5 2 x 5 1 x y
3. Find the six trig functions of each of the following angles: a. 135o 5 b. 6 1 4. Given that sin = and is in quadrant IV, find the cosine and tangent of . 2 5. Convert 124o into radians. 7 6. Convert 8 radians into degrees.
Trigonometry Review
Workshop 2
Last time we saw the definitions of the six trig. functions and evaluated them for some special angles. There are a few more "nice" angles which we will discuss here. Another way to define the functions sin and cos is as follows. If we look at the unit circle below,
(0,1)
(x,y)
1 (-1,0) (1,0)
(0,-1)
and let (x,y) be any point on the circle, then and cos=x, and sin =y. To see this simply examine the triangle above and use the previous definitions of these functions. Thus to find the sines and cosines of angles we only need to find the x and y components of the point on the unit circle that corresponds to that angle. Hence we see that: cos0o = 1 sin 0o = 0 cos 90o = 0 sin 90o = 1 cos 180o = 1 sin 180o = 0 cos 270o = 0 sin 270o = 1
Since we know the sines and cosines for these angles we can find values for the other six trig functions: Fill in these for 0o and 90o below: tan 0o = __________ cot 0o = __________ sec 0o = __________ csc 0o = __________ tan 90o = __________ cot 90o = __________ sec 90o = __________ csc 90o = __________
At this point you should be able to calculate the trig functions of all angles with reference angles of 30o, 45o, 60o, as well as all multiples of 90o. For other angle it will be necessary to use a calculator. Don't forget to put your calculator in the appropriate mode (either degrees or radians) depending on which you are using.
Trigonometric Identities: The following are some of the major trig identities which you will need to know. This list is NOT a complete list of all trig identities, simply the important ones. Pythagorean Identities: sin2 + cos2 = 1 1 + cot 2 = csc2 tan2 + 1 = sec2
(Note that the last two can be derived from the first by dividing by either sin2 or cos2)
Addition formulas: sin(AB) = sinAcosB cosAsinB cos(AB) = cosAcosB + sinAsinB
(Note that for the cosine addition formula the +/- are reversed)
If we let A=B in the above formulas and choose the "+" we get the Double Angle Identities: sin(2A) = 2sinAcosA cos(2A) = cos 2A - sin2A In addition we have the following laws which apply to triangles: A Law of Cosines: a2 = b2+ c2 -2bc cosA c b Law of Sines: B sinA sinB sinC = = a C a b c Practice Exercises #2: 1. Find all sides and angles in the following triangles: a. b.
10 o 45 a
4
30o
120o
a b
2. If sin(A) = 1/3 and A is in quadrant II, find: (a) sin(2A); (b) cos(2A); (c) tan(2A) 3. Solve for all values of 0 x 2 that satisfy: (a) sin x = 4. Verify the identity sin2 + cos2 = 1 for =120. 5. Find the six trig functions of 180o 3 2 (b) 2cosx sinx = sinx
Trigonometry Review This time we will look at the graphs of y = sin(x) and y = cos(x), as well as some variations.
Workshop 3
Recall last time we defined the functions sin and cos is as follows. If we look at the unit circle below,
(0,1) (x,y)
1 (-1,0) (1,0)
(0,-1)
and let (x,y) be any point on the circle, then and cos=x, and sin =y. Notice that as we move around the circle y = sin(x), which measures the y value of the point starts at 0 and increases to 1 at x = /2. Cosine however, which measures the x value of the point starts at 1 then decreases to 0 at x = /2. They are both described in the tables below:
x 0 /2 3 /2 2 y = sin(x) 0 1 0 -1 0 y = cos(x) 1 0 -1 0 1
Thus we have the following graphs of y = sin(x), and y = cos (x) respectively:
y = sin(x)
y = cos (x)
Now what happens if we change things a bit? For example, let's look at the graph of y = 2sin(x). If we complete the chart as we did above we have:
x 0 /2 3 /2 2
y = sin(x) 0 1 0 -1 0
y = 2sin(x) 0 2 0 -2 0
and the graph:
The graph has effectively been stretched vertically. This stretch changes the aplitude of the graph. The Amplitude of y = Asin(x) is |A|. Now let's consider that graph of y = sin(2x). Notice that this differs from the above function in that the 2 is inside that sine (not outside).
x 0 /4 /2 3 /4 2x 0 /2 3 /2 2 y = sin(2x) 0 1 0 -1 0
Notice that the graph has been "shrunk" horizontally by 1/2. This changes the period of the function (or the distance before the function begins repeating itself).
In general the period of y = sin(Bx) is 2 / B. Consider the graph of y = sin(x)+1. Notice that we are simply adding one to the y-value for each x-value. This has the effect of shifting the graph vertically by one:
As our last example consider the function y = cos(x - /2). Since we are subtracting from the x-value (not the y-value) this will shift the graph horizontally. Although it might seem reasonable to expect a shift to the left, the graph will be shifted to the right. The easiest way to determine the shift is to set the angle of the funtion to zero. In this case that means setting x- /2 = 0 and so x = /2. Thus the shift is to the right by a positive /2, and we have the graph:
Practice Excercises #3: 1. Find the period of each of the following: (a) y = sin(5x) (b) y = cos (x/2) (c) y = sin ( x) 2. Graph each of the following on a seperate axis. (a) y = 2 sin (4x); (b) y = cos(2 x)+1; (c) y = 3 sin (x + ) 3. Find an example of a sine function which has an amplitude of 3, period of 5 and passes through the point (0,4)
Trigonometry Review
Workshop 4
In this workshop we will continue to discuss solving trigonometric equations and further identites. Example : Solve sin2 x = 1 for all 0 x < 2 . Solution: This problem is very similar to solving the equation y2 =1 and should be thought of as similar. There are two ways to approach solving it. One is to take the square root of both sides. The other is to put everything on one side and factor. The latter provides a more general way so that is the approach that will be taken here. sin2 x = 1 sin2 x - 1 = 0 (sin x +1)(sin x-1) = 0. Hence we have sin x = 1 or sin x = 1. Recall that the sine represents the vertical distance on the unit circle. By examining the unit circle we see that sin x = 1 when x = /2 and sin x = 1 when x = 3 /2 radians. Hence, the solutions set is { /2,3 / 2 }. Notice that we do not include 2 , since it is not in the interval 0 x < 2 . Example : Solve cos 2x = 1, where 0 x < 2 . There are several ways to approach this problem. One possible way would be to use the double angle formula for cosine. Let's solve the problem this way, then consider a different approach. cos2x = 1 cos2 x sin2 x = 1 (1sin2 x) sin2 x = 1 12sin2 x = 1 2sin2 x = 0 sin2 x = 0 sin x = 0. Since sin x = 0 at x = 0 and x = , our solution set is {0, }. There is, however, another approach to this problem. Since 2x is the angle, let's solve for 2x first. Notice that cos 2x has a period of 2 . Hence, to any solution we obtain, we can add the period of this function and this will give us another solution. In solving cos 2x = 1 notice that there is only one place where the cosine is zero and that is at 0 radians. Hence, 2x=0, and thus x=0. Adding one period to this answer gives a second answer 0+ = . Hence the solutions are x = 0 and x = radians. Notice that if we add again we get + = 2 , which is outside the range of answers we want. The solution set {0, } is complete. Notice that this agrees with the answer above. Example : Solve sin2 3x = 1 for 0 x < 2 . Solution: First take the square root of both sides to obtain sin 3x = 1. That is, sin 3x = 1, or sin3x = 1. The sin = 1 at = /2 and the sin = 1 at = 3 /2. Hence we have 3x = /2, and 3x = 3 /2, or x = /6, and x = /2. Again, this is not a complete set of solutions. The period of sin 3x is 2 /3 and this needs to be added to each solution until the values exceed 2 . Hence another solution is /6+2 /3 = 5 /6. Continuing this process, we obtain the complete set of solutions: x { /6, /2, 5 /6, 7 /6, 3 /2, 11 /6}.
More Identities Trig identities play an important part in calculus. Being able to identify the major ones, especially the double angle formulas and the famous sin2 x + cos2 x=1 is very important. There are, however, many other useful identities which can be proven using definitions and existing identities. For example, it can be shown that cos2x + 2sin2 x = 1. To show this, start with one side and try to reduce it to the other. For this example (and in general) it is generally easier to start with the more difficult side and try to simplify it. Start by using the double angle formula for cosine: cos2x + 2sin2 x = (cos2 x-sin2 x)+2sin2 x , = cos2 x + ( sin2 x + 2sin2 x) , = cos2 x + sin2 x , = 1. Example : Prove the identity (sec x)(cot x)(csc x) = csc2 x. Solution: Beginning with the left hand side, and using the basic definitions of the trig functions we find: 1 cos x 1 (sec x)(cot x)(csc x) = cos x sin x sin x 1 = 2 = csc2 x . sin x Practice Excercises #4: 1. Solve each of the following trigonometric equations: (a) sin(2x) = 1/2 (c) cos2 x + sin x = 1 2. Verify each of the following identities: (a) (sin x) (sec x) = tan x (c) tan x sec x = 2 1 cos x sin x (b) (tan x)(sin 2x) = 2 sin2 x (d) cos4 x sin4 x = 1-2sin2 x. (b) sec2 (3x)=2 (d) tan (4x) = 3
Solutions to Problem Set #1:
60o= 3 2. (a) -1 26 sin =
1. sin 60 o =
3 1 2 1 , sec 60o = 2, cos 60o = , csc 60o = , cot 60o = , tan 2 2 3 3
21 5 2 5 21 2 , csc = , cos = , sec = , tan = , cot = , 5 5 2 2 21 21 5 26 , sec = 26 -1 , tan = , cot = -5, 5 5 3. sin(135) =
(b) sin =
, csc = - 26 , cos =
2 , csc(135) 2
2 = 2 , cos(135) = , sec(135) = 2 , tan(135) = 1, cot(135) = 1; sin(5 /6) = 1/2, sec(5 /6) = 2, cos(5 /6) = 2
3 / 2 , sec(5 /6) = 2/ 3 , tan (5 /6) = 1/ 3 , cot(5 /6) = 3 4.
6. 7 radians = 157.5 o 8
cos =
31 radians, 45
3 1 , tan = , 2 3
5. 124 o =
Solutions to Problem Set #2:
(1) (a) a = b = 5 2, = 45 o (2) (a) 4 2 9 (b) 7 9 (c) (b)a = 4, b = 30o , c = 4 3 4 2 7 3 , , 5 3
(3) (a) x =
2 , 3 3
(b) x = 0,
(4) sin2 120 + cos2 120 = (
3 2 1 3 1 ) + ( )2 = + = 1. 2 4 4 2 o o o (5) sin(180 ) = 0, cos(180 ) = 1, tan(180 ) = 0, o o o csc(180 ) is undefined, sec(180 ) = 1, cot(180 ) is undefined.
Solutions to Problem Set #3:
1. (a) 2 /5, (b) 4 , (c) 2 2.
(a)
2 /2 x 1 x y
(b)
2
(c)
y 3
3 x
3. y = 3sin
2 5 x + 4
1. (a) x = /12, 5 /12, 13 /12, 17 /12 (b) x = /12, 3 /12, 5 /12, 7 /12, 9 /12, 11 /12, 13 /12, 13 /12, 15 /12, 17 /12, 19 /12, 21 /12, 23 /12. (c) x = 0, /2, (d) x = /3, 5 /6, 4 /3, 11 /6
Solutions to Problem Set #4
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5822)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1093)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (852)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (898)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (349)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (403)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Electrical Cheat SheetDocument10 pagesElectrical Cheat SheetM J Rhoades67% (6)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Six Trigonometric RatiosDocument4 pagesSix Trigonometric RatiosJomar Gregorio100% (10)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Formulas For EE 201Document3 pagesFormulas For EE 201berickson_14No ratings yet
- Logic Gates-Boolean Algebra-Karnaugh MapDocument1 pageLogic Gates-Boolean Algebra-Karnaugh Mapberickson_14No ratings yet
- EE-2110 - Formula SheetDocument2 pagesEE-2110 - Formula Sheetberickson_14No ratings yet
- Trig Cheat SheetDocument4 pagesTrig Cheat Sheetapi-284574585No ratings yet
- θ α - alpha β - beta γ - gamma: theta Obtuse Angle Between 90 & 180Document8 pagesθ α - alpha β - beta γ - gamma: theta Obtuse Angle Between 90 & 180charmaine padorNo ratings yet
- The Trigonometric Functions We Will Be Looking At: Sine Cosine TangentDocument23 pagesThe Trigonometric Functions We Will Be Looking At: Sine Cosine TangentGenne kayeNo ratings yet
- Induction ProblemsDocument2 pagesInduction ProblemsMaged SamuelNo ratings yet
- Ba136 PDFDocument293 pagesBa136 PDFZen AlkaffNo ratings yet
- Practice Problem No. 2Document8 pagesPractice Problem No. 2AaRichard ManaloNo ratings yet
- Maths Class 11 HOTS Important Question 22Document8 pagesMaths Class 11 HOTS Important Question 22srinidhiNo ratings yet
- James Ruse 2005 3U TrialDocument7 pagesJames Ruse 2005 3U TrialEmilyWongNo ratings yet
- Trig 1 NotesDocument7 pagesTrig 1 NotesMrs. HedrickNo ratings yet
- Pre - Calculus - Module 7Document15 pagesPre - Calculus - Module 7Sharlene Mae BuitizonNo ratings yet
- Phy 105 Problem Set 1 Solutions 2012Document9 pagesPhy 105 Problem Set 1 Solutions 2012pbrowning9416No ratings yet
- The Expert TA - 3aaDocument6 pagesThe Expert TA - 3aaMuzamil ShahNo ratings yet
- MAT 461, Prof. Swift The Fourier Cosine Series of sin (πx/L)Document2 pagesMAT 461, Prof. Swift The Fourier Cosine Series of sin (πx/L)NITIN KUMARNo ratings yet
- Vector Algebra Tutorial QuestionsDocument5 pagesVector Algebra Tutorial QuestionsmubbaahNo ratings yet
- SurveyingDocument11 pagesSurveyingRobin TubleNo ratings yet
- Final Exam Review CummulativeDocument33 pagesFinal Exam Review CummulativeAj Koenig0% (1)
- Calculus Reference and NotesDocument3 pagesCalculus Reference and NotesLexy TeoNo ratings yet
- Fourier Integrals and Fourier TransformsDocument7 pagesFourier Integrals and Fourier TransformsVraj MehtaNo ratings yet
- Testlab Software Reference Manual - Functions and FormulasDocument12 pagesTestlab Software Reference Manual - Functions and Formulasmuhammad irfanNo ratings yet
- Digital Compensator Design For LLC Resonant ConverterDocument28 pagesDigital Compensator Design For LLC Resonant ConverterVũ Hùng TrángNo ratings yet
- c3 TrigonometryDocument13 pagesc3 Trigonometryazmat18No ratings yet
- Lecture 05 Complex Number Part 01Document54 pagesLecture 05 Complex Number Part 01Logix FicsarioNo ratings yet
- Self-Assessment: 8 Circular Measure and Trigonometric FunctionsDocument2 pagesSelf-Assessment: 8 Circular Measure and Trigonometric FunctionsboostoberoiNo ratings yet
- Sheets Matlab 2Document1 pageSheets Matlab 2Mahmoud EldabahNo ratings yet
- PDFDocument207 pagesPDFPaulmoNo ratings yet
- sin α cos α 1 + = a b a + bDocument13 pagessin α cos α 1 + = a b a + bvedfhgjsljgNo ratings yet
- Bk5 Sol C14 EDocument36 pagesBk5 Sol C14 EMa Ka YiNo ratings yet
- Trigonometry Exact Values: IGCSEDocument26 pagesTrigonometry Exact Values: IGCSEZoon AANo ratings yet
- The Sine and Cosine Rule Worksheets Questions and Revision MMEDocument1 pageThe Sine and Cosine Rule Worksheets Questions and Revision MMEmohitNo ratings yet
- Higher 2 Mathematics: Paper 1Document6 pagesHigher 2 Mathematics: Paper 1Seng SoonNo ratings yet