Professional Documents
Culture Documents
Fourier Transform of A Rectangular Pulse Function
Fourier Transform of A Rectangular Pulse Function
Uploaded by
aliqpskOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Fourier Transform of A Rectangular Pulse Function
Fourier Transform of A Rectangular Pulse Function
Uploaded by
aliqpskCopyright:
Available Formats
Fourier Transform of a Rectangular Pulse Function
The rectangular pulse function (RPF) is dened as
(t) =
_
1
2
t <
2
0 else
.
The Fourier transform of the RPF is calculated as follows,
P
() = F [
(t)] ,
=
_
(t) dt,
=
_
2
2
e
jt
dt,
=
1
j
e
jt
2
,
=
j
_
e
j
2
e
j
2
_
.
Since we know from Eulers equations that Ae
j
= A, we may represent the complex value in trigonometric terms, Ae
j
=
Acos() + jAsin(). Substituting this into the above, we nd,
P
() =
j
_
cos
_
2
_
+ jsin
_
2
_
cos
_
2
_
jsin
_
2
__
.
Now, since basic trigonometry tells us that cos() = cos() and sin() = sin(), we obtain
P
() =
j
_
cos
_
2
_
jsin
_
2
_
cos
_
2
_
jsin
_
2
__
,
=
2
_
j
2
_
sin
_
2
_
,
=
2
sin
_
2
_
.
The nal solution above is cumbersome to work with, as it is of the form g(x) =
f(x)
x
. So, we will convert the above solution
to be in terms of the sinc function which is dened as
sinc(a) =
sin(a)
a
.
We now work our solution for the Fourier Transform of the RPF to be in terms of sinc,
P
() =
2
sin
_
_
,
=
2
sin
_
2
__
,
=
2
sin
_
2
__
2
_
2
_,
=
2
2
__
sin
_
2
__
2
_ ,
=
sin
_
2
__
2
_ ,
= sinc
_
2
_
.
And so, with the above, we have found a simple expression for the Fourier transform of the RPF
(t) = F
1
_
sinc
_
2
__
,
F [
(t)] = sinc
_
2
_
.
You might also like
- Chapter 4 Continuous-Time Fourier Transform: ELG 3120 Signals and SystemsDocument26 pagesChapter 4 Continuous-Time Fourier Transform: ELG 3120 Signals and SystemsAkshay JindalNo ratings yet
- Fourier TransformDocument20 pagesFourier Transformraushankumar201No ratings yet
- 1 Properties of L Fourier TransformDocument4 pages1 Properties of L Fourier TransformAmit BisaiNo ratings yet
- Laplace and Fourier Transforms: P.C. Chau, UCSD C 2000Document2 pagesLaplace and Fourier Transforms: P.C. Chau, UCSD C 2000MachodogNo ratings yet
- Convolution FT 0Document29 pagesConvolution FT 0Fazly MohdNo ratings yet
- Fourier TransformDocument35 pagesFourier TransformThanatkrit KaewtemNo ratings yet
- Optimal Filtering1Document6 pagesOptimal Filtering1mutaz099No ratings yet
- PendelDocument11 pagesPendelLeo KutsNo ratings yet
- Mathematical Techniques III (PHY 317) Answers For Exercise Class 8Document5 pagesMathematical Techniques III (PHY 317) Answers For Exercise Class 8Tri Phương NguyễnNo ratings yet
- P1 MT (Abr)Document5 pagesP1 MT (Abr)fikrianyNo ratings yet
- Bochner's Theorem On The Fourier Transform On RDocument9 pagesBochner's Theorem On The Fourier Transform On REdgar MarcaNo ratings yet
- Adaptive Lecture04 2005Document28 pagesAdaptive Lecture04 2005Cuter HsuNo ratings yet
- Lecture 6 PDFDocument13 pagesLecture 6 PDFAbd Elmohsen MustafaNo ratings yet
- Discrete Linear Model Following Systems: Kybernetika - Volume13 (1977), Number5Document10 pagesDiscrete Linear Model Following Systems: Kybernetika - Volume13 (1977), Number5Koti GaddamNo ratings yet
- Fractional Fourier Transform: Introduction and ExplorationDocument11 pagesFractional Fourier Transform: Introduction and ExplorationIan Hoover100% (1)
- Enhanced Eudml Content Accessible Layered PDF Eudml 49037 0Document12 pagesEnhanced Eudml Content Accessible Layered PDF Eudml 49037 0Youssef S. DablizNo ratings yet
- Fourier TransformsDocument12 pagesFourier TransformsKajal KhanNo ratings yet
- Appendix A The Laplace Transform: F(S) So ThatDocument29 pagesAppendix A The Laplace Transform: F(S) So ThatMuhammed IfkazNo ratings yet
- Ch#5 The Two-Sided Laplace TransformDocument19 pagesCh#5 The Two-Sided Laplace TransformMubarak AhmadNo ratings yet
- Error Bounds For Approximation With Neural Networks: AbstractDocument11 pagesError Bounds For Approximation With Neural Networks: AbstractsadyehclenNo ratings yet
- Chapter 4Document15 pagesChapter 4man-895142No ratings yet
- Science I Tutorial: - Fourier and Laplace TransformsDocument22 pagesScience I Tutorial: - Fourier and Laplace Transformsdeep_red_rosieNo ratings yet
- Lecture 1 Fermi Liquid TheoryDocument25 pagesLecture 1 Fermi Liquid TheoryEMMABOICUNo ratings yet
- 523 M1380: Adaptive Control Systems Lecture 5: Sufficiently Rich Signals and Parameter ConvergenceDocument6 pages523 M1380: Adaptive Control Systems Lecture 5: Sufficiently Rich Signals and Parameter ConvergenceCuter HsuNo ratings yet
- Application of Laplace TransformDocument35 pagesApplication of Laplace TransformSingappuli100% (1)
- AnandDocument11 pagesAnandNandani Candy DcostaNo ratings yet
- La Place TransformDocument8 pagesLa Place Transformreliance2012No ratings yet
- Solutions To ExercisesDocument54 pagesSolutions To ExercisesNelsonNo ratings yet
- A Proof That B Splines With Equal Spacing Have Mirow SymmetryDocument4 pagesA Proof That B Splines With Equal Spacing Have Mirow SymmetryJohn BreckonNo ratings yet
- 6 6 6 6 Topic Topic Topic Topic: Laplace Transforms Laplace Transforms Laplace Transforms Laplace TransformsDocument23 pages6 6 6 6 Topic Topic Topic Topic: Laplace Transforms Laplace Transforms Laplace Transforms Laplace TransformsManpreet SinghNo ratings yet
- Power Spectral DensityDocument2 pagesPower Spectral DensityAshwin UmeshNo ratings yet
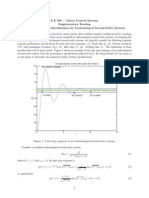
- E E 380 - Linear Control Systems Supplementary Reading Transient Response Specifications For Underdamped Second-Order SystemsDocument4 pagesE E 380 - Linear Control Systems Supplementary Reading Transient Response Specifications For Underdamped Second-Order SystemsMOdy SrkNo ratings yet
- Image Enhancement in Frequency DomainDocument17 pagesImage Enhancement in Frequency DomainSuresh Kumar VermaNo ratings yet
- Dynamic Properties of Dielectrics E F (T) : P + P (T) 0 P (T) (P P)Document24 pagesDynamic Properties of Dielectrics E F (T) : P + P (T) 0 P (T) (P P)Fari PratomosiwiNo ratings yet
- Two-Step Methods For Numerical Solution of Fuzzy Differential EquationsDocument12 pagesTwo-Step Methods For Numerical Solution of Fuzzy Differential EquationsKelvin FookNo ratings yet
- Fourier Integrals: 2.1 L - TheoryDocument31 pagesFourier Integrals: 2.1 L - TheoryRiio MardhaniNo ratings yet
- University of Manchester CS3291: Digital Signal Processing 2003/2004Document11 pagesUniversity of Manchester CS3291: Digital Signal Processing 2003/2004Mukesh KumarNo ratings yet
- Noncentral Hypergeometric Distribution: J S M J M PDocument6 pagesNoncentral Hypergeometric Distribution: J S M J M PjuntujuntuNo ratings yet
- F AnalysDocument16 pagesF Analysjcpa1000No ratings yet
- Differential Equations & Integral TransformsDocument192 pagesDifferential Equations & Integral Transformscyours70No ratings yet
- 5.74 Time-Dependent Quantum Mechanics: R, T I R, TDocument12 pages5.74 Time-Dependent Quantum Mechanics: R, T I R, Tdebashis22mNo ratings yet
- Fourier TransformDocument21 pagesFourier TransformPrudvi RajNo ratings yet
- Fourier Transform and Plancherel TheoremDocument34 pagesFourier Transform and Plancherel Theoremgogo222No ratings yet
- R&solution Numhique D'une Equation de Fokker-Planck Ionique Avec Temphature HlectroniqueDocument6 pagesR&solution Numhique D'une Equation de Fokker-Planck Ionique Avec Temphature HlectroniquempekNo ratings yet
- Periodic Functions, The Unit Step Function and The Second Shifting TheoremDocument21 pagesPeriodic Functions, The Unit Step Function and The Second Shifting TheoremChristian SarmientoNo ratings yet
- Time Harmonic Waves: Representation in Phasor DomainDocument13 pagesTime Harmonic Waves: Representation in Phasor DomainSerkan KaradağNo ratings yet
- Set 7Document25 pagesSet 7Lokesh KancharlaNo ratings yet
- Supplementary notes on Fourier series and Hilbert spaces: p C p C 2 C 1 C p C q C p C 2 C 2π 2πDocument3 pagesSupplementary notes on Fourier series and Hilbert spaces: p C p C 2 C 1 C p C q C p C 2 C 2π 2πEmpedoklessandalNo ratings yet
- SBEIII HW2 KeyDocument4 pagesSBEIII HW2 KeyRichard ChenNo ratings yet
- System Dynamics OgataDocument200 pagesSystem Dynamics Ogatalokooh100% (2)
- Bounds of Operator Functions and Furuta Inequalities: Publ. RIMS, Kyoto UnivDocument8 pagesBounds of Operator Functions and Furuta Inequalities: Publ. RIMS, Kyoto Univtdtv0204No ratings yet
- Transformada de FourierDocument9 pagesTransformada de Fourierjose2017No ratings yet
- Fourier Series and TransformDocument46 pagesFourier Series and TransformVaibhav Patil100% (1)
- PEC Fourier Özgür ÜstünDocument17 pagesPEC Fourier Özgür ÜstünBatuhan IzmırlıNo ratings yet
- Circuits 10 5Document3 pagesCircuits 10 5K0dOrN4No ratings yet
- Harmonic Maps and Minimal Immersions with Symmetries (AM-130), Volume 130: Methods of Ordinary Differential Equations Applied to Elliptic Variational Problems. (AM-130)From EverandHarmonic Maps and Minimal Immersions with Symmetries (AM-130), Volume 130: Methods of Ordinary Differential Equations Applied to Elliptic Variational Problems. (AM-130)No ratings yet
- DesigningHighspeedSequentialCircuits DraftDocument15 pagesDesigningHighspeedSequentialCircuits DraftaliqpskNo ratings yet
- AnXNOR BasedDouble Edge TriggeredFlip FlopforTwo PhasePipelinesDocument7 pagesAnXNOR BasedDouble Edge TriggeredFlip FlopforTwo PhasePipelinesaliqpskNo ratings yet
- Complete Floor Coverage in Cleaning Robots Using Lateral Ultrasonic SensorsDocument4 pagesComplete Floor Coverage in Cleaning Robots Using Lateral Ultrasonic SensorsaliqpskNo ratings yet
- Postulates of Quantum MechanicsDocument1 pagePostulates of Quantum MechanicsaliqpskNo ratings yet
- Notes OpampDocument26 pagesNotes OpampmamadhubalaNo ratings yet
- Sin CSC: Trigonometric Functions and DerivativesDocument4 pagesSin CSC: Trigonometric Functions and DerivativesaliqpskNo ratings yet
- The Detection of Fault-Prone Program Using A Neural NetworkDocument6 pagesThe Detection of Fault-Prone Program Using A Neural NetworkaliqpskNo ratings yet
- Lcleeresume 2008Document9 pagesLcleeresume 2008aliqpskNo ratings yet