Scribd Logo
Upload

Welcome to Scribd!

  • 5 views

    Extract Pages From 2

    Uploaded by

    Xivel Sulistyo
    The document provides instructions to calculate the velocity and acceleration of a turtle moving with constant negative acceleration. It gives the initial position, velocity, and acceleration and calculates: (1) the time when velocity is zero; (2) the times when position returns to the starting point; (3) the times and velocities when position is at specific values; and (4) sketches the position, velocity, and acceleration graphs.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content

    You might also like

    Extract Pages From 2

    Uploaded by

    Xivel Sulistyo
    5 views1 page
    The document provides instructions to calculate the velocity and acceleration of a turtle moving with constant negative acceleration. It gives the initial position, velocity, and acceleration and calculates: (1) the time when velocity is zero; (2) the times when position returns to the starting point; (3) the times and velocities when position is at specific values; and (4) sketches the position, velocity, and acceleration graphs.

    Original Description:

    exta pae 222 error

    Copyright

    © Attribution Non-Commercial (BY-NC)

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    Report this Document
    The document provides instructions to calculate the velocity and acceleration of a turtle moving with constant negative acceleration. It gives the initial position, velocity, and acceleration and calculates: (1) the time when velocity is zero; (2) the times when position returns to the starting point; (3) the times and velocities when position is at specific values; and (4) sketches the position, velocity, and acceleration graphs.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    Download as pdf or txt
    5 views1 page

    Extract Pages From 2

    Uploaded by

    Xivel Sulistyo
    The document provides instructions to calculate the velocity and acceleration of a turtle moving with constant negative acceleration. It gives the initial position, velocity, and acceleration and calculates: (1) the time when velocity is zero; (2) the times when position returns to the starting point; (3) the times and velocities when position is at specific values; and (4) sketches the position, velocity, and acceleration graphs.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    Download as pdf or txt
    of 1

    2.15.

    IDENTIFY and SET UP: EXECUTE:

    Use vx "

    dx dv and ax " x to calculate vx (t ) and ax (t ). dt dt

    vx "

    dx " 2.00 cm/s $ (0.125 cm/s 2 )t dt

    dvx " $0.125 cm/s 2 dt (a) At t " 0, x " 50.0 cm, vx " 2.00 cm/s, ax " $0.125 cm/s 2 . ax "
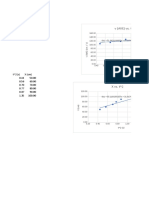
    (b) Set vx " 0 and solve for t: t " 16.0 s. (c) Set x " 50.0 cm and solve for t. This gives t " 0 and t " 32.0 s. The turtle returns to the starting point after 32.0 s. (d) Turtle is 10.0 cm from starting point when x " 60.0 cm or x " 40.0 cm. Set x " 60.0 cm and solve for t: t " 6.20 s and t " 25.8 s. At t " 6.20 s, vx " #1.23 cm/s.

    At t " 25.8 s, vx " $1.23 cm/s. Set x " 40.0 cm and solve for t: t " 36.4 s (other root to the quadratic equation is negative and hence nonphysical). At t " 36.4 s, vx " $2.55 cm/s. (e) The graphs are sketched in Figure 2.15.

    Figure 2.15 EVALUATE: The acceleration is constant and negative. vx is linear in time. It is initially positive, decreases to zero, and then becomes negative with increasing magnitude. The turtle initially moves farther away from the origin but then stops and moves in the $ x -direction.

    You might also like