Professional Documents
Culture Documents
projected conic C ceiling plane directrix: r V d β L
projected conic C ceiling plane directrix: r V d β L
Uploaded by
linghuchongCopyright:
Available Formats
You might also like
- Lab Report - Determining Coefficient of DischargeDocument9 pagesLab Report - Determining Coefficient of DischargeNikhil Penchalwar100% (2)
- OTHER CURVES ON A CONE. Conic Sections Are Widely Studied, But ThereDocument1 pageOTHER CURVES ON A CONE. Conic Sections Are Widely Studied, But TherelinghuchongNo ratings yet
- RollingConesCylinders Part15Document1 pageRollingConesCylinders Part15linghuchongNo ratings yet
- Greens Theorem ProofDocument5 pagesGreens Theorem ProofGaurav DharNo ratings yet
- Theorem 6. If The Ceiling Projection of Curve CDocument1 pageTheorem 6. If The Ceiling Projection of Curve ClinghuchongNo ratings yet
- RollingConesCylinders Part14Document1 pageRollingConesCylinders Part14linghuchongNo ratings yet
- Vectors and The Geometry of Space 12.5. Lines and Planes in SpaceDocument4 pagesVectors and The Geometry of Space 12.5. Lines and Planes in SpaceKing CreativeNo ratings yet
- Alg Curves 4Document59 pagesAlg Curves 4Marcelo RodriguesNo ratings yet
- Geometry ProjectDocument26 pagesGeometry ProjectAnchana VMNo ratings yet
- Line Integrals: X X (T) y y (T) ADocument76 pagesLine Integrals: X X (T) y y (T) AFãďhü Aŕŕåżi HãśibůàñNo ratings yet
- Equations of Lines and PlanesDocument26 pagesEquations of Lines and PlanesJerry Essen100% (1)
- Summary CH 9Document17 pagesSummary CH 9lzyabc597No ratings yet
- Note. The Ratio E: Focus Directrix LDocument1 pageNote. The Ratio E: Focus Directrix LlinghuchongNo ratings yet
- Lecture 10Document3 pagesLecture 10ThetaOmegaNo ratings yet
- Commalg 2013 c9 PDFDocument11 pagesCommalg 2013 c9 PDFyacp16761No ratings yet
- Ulseb/Uleac Special Paper Pure Mathematics QuestionsDocument19 pagesUlseb/Uleac Special Paper Pure Mathematics Questionsalphamale173No ratings yet
- StewartCalcET8 12 05Document36 pagesStewartCalcET8 12 05OhoodKAlesayiNo ratings yet
- Caltech Vector Calculus 3Document13 pagesCaltech Vector Calculus 3nislam57No ratings yet
- Calculus NilDocument7 pagesCalculus NilPushpak ShewaleNo ratings yet
- RollingConesCylinders Part25Document1 pageRollingConesCylinders Part25linghuchongNo ratings yet
- Line IntegralsDocument7 pagesLine IntegralsTeresa Villena GonzálezNo ratings yet
- L10Document4 pagesL10Srushti AgarwalNo ratings yet
- Helix Equations 1 PDFDocument21 pagesHelix Equations 1 PDFRohitMadkeNo ratings yet
- 3.1. Control SurveyDocument24 pages3.1. Control SurveyLanestosa Ernest Rey B.No ratings yet
- Theorem 1. For A Curve C As Described, The Profile Equation PDocument1 pageTheorem 1. For A Curve C As Described, The Profile Equation PlinghuchongNo ratings yet
- Straight Lines: Various Forms of The Equation of A LineDocument7 pagesStraight Lines: Various Forms of The Equation of A LineSowjanya VemulapalliNo ratings yet
- MA111 Lec9 D3D4Document13 pagesMA111 Lec9 D3D4pahnhnykNo ratings yet
- Lecture Notes For MA5NO Cohomology, Connections, Curvature and Characteristic ClassesDocument66 pagesLecture Notes For MA5NO Cohomology, Connections, Curvature and Characteristic ClassesSrinivas RauNo ratings yet
- Vector AlgebraDocument39 pagesVector AlgebraKuntal Satpathi100% (1)
- 3.2 Constructible NumbersDocument10 pages3.2 Constructible NumbershGanieetNo ratings yet
- Sard's Theorem General ProofDocument7 pagesSard's Theorem General ProofDennis MetelskyNo ratings yet
- 07 - Chapter 1Document15 pages07 - Chapter 1sp thipathiNo ratings yet
- Curves Do Carmo NotesDocument7 pagesCurves Do Carmo NotesDharil ShahNo ratings yet
- Microsoft PowerPoint - 4. ELMAG - 1 - Vector CalculusDocument86 pagesMicrosoft PowerPoint - 4. ELMAG - 1 - Vector CalculusDeni RistiantoNo ratings yet
- Desargues Involution TheoremDocument6 pagesDesargues Involution TheoremDavis Suarez PajueloNo ratings yet
- Multivariable Knill 2019 PDFDocument117 pagesMultivariable Knill 2019 PDFjun lideNo ratings yet
- Simple Curves or Circular Curves 04 11 2015Document124 pagesSimple Curves or Circular Curves 04 11 2015HanafiahHamzahNo ratings yet
- Feedback AmplifierDocument52 pagesFeedback AmplifierBharavi K SNo ratings yet
- Geo Cross RatioDocument31 pagesGeo Cross Ratioclrgeek100% (1)
- Stokes Theorem Ii Maths21a, O. Knill: y Z Z X X y X y ZDocument1 pageStokes Theorem Ii Maths21a, O. Knill: y Z Z X X y X y Zmartim_martinsNo ratings yet
- Intersection of Line and PlaneDocument2 pagesIntersection of Line and PlaneAljon AbriamNo ratings yet
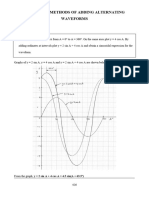
- Chapter 30 Methods of Adding Alternating Waveforms: EXERCISE 118 Page 315Document17 pagesChapter 30 Methods of Adding Alternating Waveforms: EXERCISE 118 Page 315Josh AmuraoNo ratings yet
- 4 QuasiDocument5 pages4 QuasiPloni AlmoniNo ratings yet
- Circles ProjectDocument4 pagesCircles ProjectKANISHK SajankarNo ratings yet
- Calulo IvanDocument13 pagesCalulo IvanPedro IvanNo ratings yet
- Work of Second LessonDocument4 pagesWork of Second LessonRicardo CasadoNo ratings yet
- Higher Eng Maths 9th Ed 2021 Solutions ChapterDocument22 pagesHigher Eng Maths 9th Ed 2021 Solutions ChapterAubrey JosephNo ratings yet
- Homework 5 Solutions: 2.4 - Invertibility and IsomorphismsDocument4 pagesHomework 5 Solutions: 2.4 - Invertibility and IsomorphismsCody SageNo ratings yet
- EE5121: Convex Optimization: Assignment 2Document1 pageEE5121: Convex Optimization: Assignment 2elleshNo ratings yet
- Circle Geometry: Euclid Eworkshop # 6Document6 pagesCircle Geometry: Euclid Eworkshop # 6Dhananjay KulkarniNo ratings yet
- 07 - Sample Paper - 9th - Maths - Solutions - R.N.S - 2023-24Document11 pages07 - Sample Paper - 9th - Maths - Solutions - R.N.S - 2023-24deeppratap67890No ratings yet
- CheungRault - SampleDocument10 pagesCheungRault - SampleeuclidanNo ratings yet
- Conformal MappingDocument6 pagesConformal Mappingwaku74No ratings yet
- Otto 1996Document19 pagesOtto 1996Yousef AlamriNo ratings yet
- Chapter 3Document24 pagesChapter 3Elva MaulidaNo ratings yet
- Definite IntegralDocument12 pagesDefinite IntegralJeremiahLimNo ratings yet
- Linear TransformationsDocument8 pagesLinear TransformationsVignesh RavichandranNo ratings yet
- The Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64From EverandThe Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64No ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part16Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part16linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part4Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part4linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part67Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part67linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part52Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part52linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part57Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part57linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part65Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part65linghuchongNo ratings yet
projected conic C ceiling plane directrix: r V d β L
projected conic C ceiling plane directrix: r V d β L
Uploaded by
linghuchongOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
projected conic C ceiling plane directrix: r V d β L
projected conic C ceiling plane directrix: r V d β L
Uploaded by
linghuchongCopyright:
Available Formats
Thus, if k = 1/ sin , the unwrapped image of C on a plane has polar equation R () = with R (0) = kr (0). Proof.
. Let L denote the line of intersection of the cutting plane and ceiling plane. For any point P on C let P0 denote its projection on C0 . Let d be the distance from P0 to L and r the distance from P0 to V , as depicted in Figure 19. R (0) , 1 + sin(k ) (23)
projected conic C0 V r
ceiling plane directrix P0 d L h cutting plane
P B
conic C
Figure 19. Diagram for proving parts (a), (b), and (c) of Theorem 7. (The ceiling plane intersects the cutting plane along the directrix L of the projected conic.)
We now show that the ratio r /d is tan tan , a constant (independent of P0 ) that we denote by . This will prove (a), (b), and (c). Write the ratio r /d as r r h = , d h d where h is the distance from P to P0 . From Figure 19 we see r / h = tan and h /d = tan , so the foregoing equation becomes r /d = tan tan , as required. This ensures that C0 is a conic with a focus at V and directrix L . To derive (22), use the focus V as origin in the ceiling plane, and let r () denote the distance from V to the point on C0 with polar coordinates (r (), ), where is measured from a line through V parallel to L , as shown in Figure 20. We have shown that C0 is a conic with eccentricity , hence the focal denition of conic gives r () = d . But d = D r () sin , where D is the distance from the focus to the directrix, hence r () = ( D r () sin ), which implies that r () = D /(1 + sin ). When = 0 we get D = r (0), which proves (22), and (23) follows from Theorem 5. May 2007]
UNWRAPPING CURVES FROM CYLINDERS AND CONES
405
You might also like
- Lab Report - Determining Coefficient of DischargeDocument9 pagesLab Report - Determining Coefficient of DischargeNikhil Penchalwar100% (2)
- OTHER CURVES ON A CONE. Conic Sections Are Widely Studied, But ThereDocument1 pageOTHER CURVES ON A CONE. Conic Sections Are Widely Studied, But TherelinghuchongNo ratings yet
- RollingConesCylinders Part15Document1 pageRollingConesCylinders Part15linghuchongNo ratings yet
- Greens Theorem ProofDocument5 pagesGreens Theorem ProofGaurav DharNo ratings yet
- Theorem 6. If The Ceiling Projection of Curve CDocument1 pageTheorem 6. If The Ceiling Projection of Curve ClinghuchongNo ratings yet
- RollingConesCylinders Part14Document1 pageRollingConesCylinders Part14linghuchongNo ratings yet
- Vectors and The Geometry of Space 12.5. Lines and Planes in SpaceDocument4 pagesVectors and The Geometry of Space 12.5. Lines and Planes in SpaceKing CreativeNo ratings yet
- Alg Curves 4Document59 pagesAlg Curves 4Marcelo RodriguesNo ratings yet
- Geometry ProjectDocument26 pagesGeometry ProjectAnchana VMNo ratings yet
- Line Integrals: X X (T) y y (T) ADocument76 pagesLine Integrals: X X (T) y y (T) AFãďhü Aŕŕåżi HãśibůàñNo ratings yet
- Equations of Lines and PlanesDocument26 pagesEquations of Lines and PlanesJerry Essen100% (1)
- Summary CH 9Document17 pagesSummary CH 9lzyabc597No ratings yet
- Note. The Ratio E: Focus Directrix LDocument1 pageNote. The Ratio E: Focus Directrix LlinghuchongNo ratings yet
- Lecture 10Document3 pagesLecture 10ThetaOmegaNo ratings yet
- Commalg 2013 c9 PDFDocument11 pagesCommalg 2013 c9 PDFyacp16761No ratings yet
- Ulseb/Uleac Special Paper Pure Mathematics QuestionsDocument19 pagesUlseb/Uleac Special Paper Pure Mathematics Questionsalphamale173No ratings yet
- StewartCalcET8 12 05Document36 pagesStewartCalcET8 12 05OhoodKAlesayiNo ratings yet
- Caltech Vector Calculus 3Document13 pagesCaltech Vector Calculus 3nislam57No ratings yet
- Calculus NilDocument7 pagesCalculus NilPushpak ShewaleNo ratings yet
- RollingConesCylinders Part25Document1 pageRollingConesCylinders Part25linghuchongNo ratings yet
- Line IntegralsDocument7 pagesLine IntegralsTeresa Villena GonzálezNo ratings yet
- L10Document4 pagesL10Srushti AgarwalNo ratings yet
- Helix Equations 1 PDFDocument21 pagesHelix Equations 1 PDFRohitMadkeNo ratings yet
- 3.1. Control SurveyDocument24 pages3.1. Control SurveyLanestosa Ernest Rey B.No ratings yet
- Theorem 1. For A Curve C As Described, The Profile Equation PDocument1 pageTheorem 1. For A Curve C As Described, The Profile Equation PlinghuchongNo ratings yet
- Straight Lines: Various Forms of The Equation of A LineDocument7 pagesStraight Lines: Various Forms of The Equation of A LineSowjanya VemulapalliNo ratings yet
- MA111 Lec9 D3D4Document13 pagesMA111 Lec9 D3D4pahnhnykNo ratings yet
- Lecture Notes For MA5NO Cohomology, Connections, Curvature and Characteristic ClassesDocument66 pagesLecture Notes For MA5NO Cohomology, Connections, Curvature and Characteristic ClassesSrinivas RauNo ratings yet
- Vector AlgebraDocument39 pagesVector AlgebraKuntal Satpathi100% (1)
- 3.2 Constructible NumbersDocument10 pages3.2 Constructible NumbershGanieetNo ratings yet
- Sard's Theorem General ProofDocument7 pagesSard's Theorem General ProofDennis MetelskyNo ratings yet
- 07 - Chapter 1Document15 pages07 - Chapter 1sp thipathiNo ratings yet
- Curves Do Carmo NotesDocument7 pagesCurves Do Carmo NotesDharil ShahNo ratings yet
- Microsoft PowerPoint - 4. ELMAG - 1 - Vector CalculusDocument86 pagesMicrosoft PowerPoint - 4. ELMAG - 1 - Vector CalculusDeni RistiantoNo ratings yet
- Desargues Involution TheoremDocument6 pagesDesargues Involution TheoremDavis Suarez PajueloNo ratings yet
- Multivariable Knill 2019 PDFDocument117 pagesMultivariable Knill 2019 PDFjun lideNo ratings yet
- Simple Curves or Circular Curves 04 11 2015Document124 pagesSimple Curves or Circular Curves 04 11 2015HanafiahHamzahNo ratings yet
- Feedback AmplifierDocument52 pagesFeedback AmplifierBharavi K SNo ratings yet
- Geo Cross RatioDocument31 pagesGeo Cross Ratioclrgeek100% (1)
- Stokes Theorem Ii Maths21a, O. Knill: y Z Z X X y X y ZDocument1 pageStokes Theorem Ii Maths21a, O. Knill: y Z Z X X y X y Zmartim_martinsNo ratings yet
- Intersection of Line and PlaneDocument2 pagesIntersection of Line and PlaneAljon AbriamNo ratings yet
- Chapter 30 Methods of Adding Alternating Waveforms: EXERCISE 118 Page 315Document17 pagesChapter 30 Methods of Adding Alternating Waveforms: EXERCISE 118 Page 315Josh AmuraoNo ratings yet
- 4 QuasiDocument5 pages4 QuasiPloni AlmoniNo ratings yet
- Circles ProjectDocument4 pagesCircles ProjectKANISHK SajankarNo ratings yet
- Calulo IvanDocument13 pagesCalulo IvanPedro IvanNo ratings yet
- Work of Second LessonDocument4 pagesWork of Second LessonRicardo CasadoNo ratings yet
- Higher Eng Maths 9th Ed 2021 Solutions ChapterDocument22 pagesHigher Eng Maths 9th Ed 2021 Solutions ChapterAubrey JosephNo ratings yet
- Homework 5 Solutions: 2.4 - Invertibility and IsomorphismsDocument4 pagesHomework 5 Solutions: 2.4 - Invertibility and IsomorphismsCody SageNo ratings yet
- EE5121: Convex Optimization: Assignment 2Document1 pageEE5121: Convex Optimization: Assignment 2elleshNo ratings yet
- Circle Geometry: Euclid Eworkshop # 6Document6 pagesCircle Geometry: Euclid Eworkshop # 6Dhananjay KulkarniNo ratings yet
- 07 - Sample Paper - 9th - Maths - Solutions - R.N.S - 2023-24Document11 pages07 - Sample Paper - 9th - Maths - Solutions - R.N.S - 2023-24deeppratap67890No ratings yet
- CheungRault - SampleDocument10 pagesCheungRault - SampleeuclidanNo ratings yet
- Conformal MappingDocument6 pagesConformal Mappingwaku74No ratings yet
- Otto 1996Document19 pagesOtto 1996Yousef AlamriNo ratings yet
- Chapter 3Document24 pagesChapter 3Elva MaulidaNo ratings yet
- Definite IntegralDocument12 pagesDefinite IntegralJeremiahLimNo ratings yet
- Linear TransformationsDocument8 pagesLinear TransformationsVignesh RavichandranNo ratings yet
- The Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64From EverandThe Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64No ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part16Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part16linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part4Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part4linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part67Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part67linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part52Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part52linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part57Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part57linghuchongNo ratings yet
- Proposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part65Document4 pagesProposed Design Procedures For Shear and Torsion in Reinforced and Prestressed Concrete Ramirez - Part65linghuchongNo ratings yet