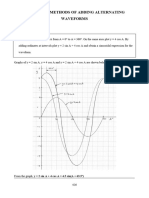
The simple relation (16), with 0 < < /2, occurs repeatedly in analyzing the shape of any curve

e unwrapped from a cone. With k = 1/ sin , (16) can be written as = k . Thus, the sine of half the vertex angle determines the relation between and . (17)

s s circular base circular arc

Figure 16. (a) Finite portion of a cone with slant height s ; (b) unwrapping the surface of this nite portion.

When the cone is cut by a plane through a diameter of the base inclined at angle , the conic section is an ellipse, parabola, or hyperbola, depending on . Figure 15a shows an ellipse, which unwraps to form a generalized ellipse that oscillates about the image of the base as shown in Figure 15b. An explicit formula for R (), which depends on both and the cones vertex angle, is given in (23). 11. REFORMULATED PROBLEM IN TERMS OF CEILING PROJECTION. In Theorem 1 we analyzed a general curve on a cylinder by projecting it onto an unwrapping plane parallel to the generators of the cylinder. To analyze a curve C lying on a cone, we project it upward onto the horizontal ceiling plane, a plane orthogonal to the axis of the cone and passing through its vertex V , as indicated in Figure 17. Curve C projects onto a curve C0 in the ceiling plane that we describe with a polar equation r = r (), where r () is the radial distance measured from vertex V as origin. The ceiling projection C0 is the prole of a vertical cylinder that intersects the cone along C . Figure 17 reveals that the two distances R () and r () satisfy r () = R () sin , where is half the vertex angle of the cone. This simple relation, together with (17), shows that the ceiling projection is the key that unlocks the basic problem. Theorem 5. Let C be a curve on the surface of a cone with vertex angle 2 . If the ceiling projection C0 has polar equation r = r (), then the unwrapped image of C has polar equation R () = kr (k ), where k = 1/ sin . Conversely, if R () is known, then (18) determines r (): r () = R (/ k )/ k . (19) (18)

Proof. The relation r () = R () sin becomes r () = R ()/ k , which in view of (17) gives (18) and (19). 402 c
THE MATHEMATICAL ASSOCIATION OF AMERICA

[Monthly 114