Professional Documents
Culture Documents
Calculus: Chain Rule (For Composition of Functions)
Calculus: Chain Rule (For Composition of Functions)
Uploaded by
Sue VanHattumOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Calculus: Chain Rule (For Composition of Functions)
Calculus: Chain Rule (For Composition of Functions)
Uploaded by
Sue VanHattumCopyright:
Available Formats
Derivatives and Composition of Functions We can now find the derivatives of most simple functions (which functions are
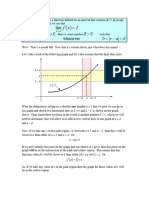
missing from our list?), but so far we have no tools for handling things like or variable. Describing Composition These functions are composed of one function inside another. For y1 we can say that and , which allows us to rewrite y1 as , showing the composition explicitly. Can you write y2 as a composition of an outer and an inner function? Experimenting by Graphing Lets look at a graph to see what the derivative of y1 might look like. Heres : , where the input to a function is more than just the
Try to graph the derivative here:
What function do you think youve graphed here?
Experimenting Algebraically Lets try to figure out how finding the derivatives of these functions might work by looking at some functions that can be simplified (unlike the two above). Example 1 To find the derivative we can multiply this out: so Example 2 and In the first example, we got our inner function back into parentheses in the derivative. Can we do that with this one? Example 3 and Can we re-write this derivative, so theres a 9 x in it? <spoiler alert> Dont look below until youve worked on the three examples above. In example 2, we get . In example 3, we get . Can you see any patterns? Lets make a table:
Can you summarize what this table shows? One way to summarize would be to make a new property of derivatives: If , then Can you come up with something? <spoiler alert> Dont turn to the next page until youve tried this.
It seems that, for
Weve come at this both graphically and algebraically. But we cant know it will always work until we prove it. The proof below is not completely sound, but its the easiest to follow that Ive found. Proving It Theorem: Given differentiable functions f and g, and Proof:
, then
Let u = g(x) and k = g(x+h) g(x). Then u+k = k+u = g(x+h). So
. At this last step, if we can replace with , then well be done. Since , though
, it seems we can deduce that this would need more detailed steps to be properly proved. Doing that gives us
. QED. Practicing It Identify the outer and inner functions. I find it helps to read a function with only the outer layer identified. For , read y = sine of something. Try these. Then do the homework in the textbook (section 2.6). 1. 2. 3. 4.
You might also like
- Composition of FunctionDocument12 pagesComposition of FunctionGoumnaamNo ratings yet
- Function Definition: Functional Programming Module 2 - Lesson 2 Introduction To Functions ObjectiveDocument7 pagesFunction Definition: Functional Programming Module 2 - Lesson 2 Introduction To Functions Objectivedorris09No ratings yet
- Math (History of Formula)Document8 pagesMath (History of Formula)ArmySapphireNo ratings yet
- A Relation Is A Set of Ordered Pairs.: Example 1Document8 pagesA Relation Is A Set of Ordered Pairs.: Example 1Norfaidah P. LondoNo ratings yet
- Chapter 3 NotesDocument34 pagesChapter 3 NotesNoreen YinNo ratings yet
- Calculus Indefinite IntegralDocument9 pagesCalculus Indefinite Integralnicusor.iacob5680No ratings yet
- Module 2 of Calculus 2Document5 pagesModule 2 of Calculus 2Jimbo J. AntipoloNo ratings yet
- Functions and GraphsDocument9 pagesFunctions and GraphsFactoran WilfredNo ratings yet
- Computers: Intuitive Calculus BlogDocument15 pagesComputers: Intuitive Calculus Blogaslam844No ratings yet
- Eulers NumberDocument38 pagesEulers NumberPraful PatilNo ratings yet
- Conservative Vector FieldsDocument9 pagesConservative Vector FieldsChernet TugeNo ratings yet
- 1.5-Inverse FunctionsDocument12 pages1.5-Inverse FunctionsOfficial-site suuNo ratings yet
- Lessson 1Document4 pagesLessson 1Tin-tin MarzanNo ratings yet
- Definition of FunctionDocument3 pagesDefinition of Functionapi-247658686No ratings yet
- Module 4 of Calculus 2Document8 pagesModule 4 of Calculus 2Jimbo J. AntipoloNo ratings yet
- Bool Bool True False False True: Lawvere's Fixed Point TheoremDocument11 pagesBool Bool True False False True: Lawvere's Fixed Point TheoremΓιάννης ΣτεργίουNo ratings yet
- Preface: Review: Inverse FunctionsDocument8 pagesPreface: Review: Inverse FunctionsYong YHNo ratings yet
- Calc No 8Document18 pagesCalc No 8qnw39257No ratings yet
- Algebraic FunctionsDocument6 pagesAlgebraic FunctionsTrisha CrushNo ratings yet
- Logarithm Functions: If B Is Any Number Such That and and ThenDocument15 pagesLogarithm Functions: If B Is Any Number Such That and and ThenCM PaulNo ratings yet
- Programming in C++ Prof. Partha Pratim Das Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Lecture - 07 Stack and Its ApplicationsDocument12 pagesProgramming in C++ Prof. Partha Pratim Das Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Lecture - 07 Stack and Its Applicationsayush guptaNo ratings yet
- Introduction To Finite Element Method Dr. R. Krishnakumar Department of Mechanical Engineering Indian Institute of Technology, Madras Lecture - 13Document23 pagesIntroduction To Finite Element Method Dr. R. Krishnakumar Department of Mechanical Engineering Indian Institute of Technology, Madras Lecture - 13mahendranNo ratings yet
- A12.1 e Complex Algebra - PPSXDocument42 pagesA12.1 e Complex Algebra - PPSXtlangiwangaNo ratings yet
- TEXTFPDocument57 pagesTEXTFPdorris09No ratings yet
- Radical WorksheetDocument38 pagesRadical WorksheetTina801No ratings yet
- Redna TaylorDocument21 pagesRedna TaylorSlavco LzNo ratings yet
- Lesson 9Document5 pagesLesson 9eduardobNo ratings yet
- Lec14 PDFDocument21 pagesLec14 PDFAbhishek AroraNo ratings yet
- Proving Countable SetsDocument3 pagesProving Countable SetsHimraj BachooNo ratings yet
- LimitDocument4 pagesLimitshahinaaslam938No ratings yet
- The Function (,) Sin Plotted by Computer: Fxy XyDocument10 pagesThe Function (,) Sin Plotted by Computer: Fxy XygdeepthiNo ratings yet
- Relation and FunctionDocument12 pagesRelation and FunctionNikka Aubrey Tegui-inNo ratings yet
- Posts CriterionDocument10 pagesPosts CriterionGaurav KhullarNo ratings yet
- AlgebraDocument39 pagesAlgebraDivya GersappaNo ratings yet
- Advanced Linear ProgrammingDocument209 pagesAdvanced Linear Programmingpraneeth nagasai100% (1)
- Lagrangian Mechanics 4Document13 pagesLagrangian Mechanics 4Sahibnoor SinghNo ratings yet
- Explicatie Raven TesteDocument9 pagesExplicatie Raven TestelutetuNo ratings yet
- Example 7 Evaluate The Following IntegralDocument5 pagesExample 7 Evaluate The Following IntegralFREDD1E77No ratings yet
- Radicals: A) Square Roots: Introduction & SimplificationDocument9 pagesRadicals: A) Square Roots: Introduction & SimplificationparamitaNo ratings yet
- Advanced Algebra IIDocument38 pagesAdvanced Algebra IIRahul ManwatkarNo ratings yet
- Swayam EngDocument34 pagesSwayam EngsriramchaudhuryNo ratings yet
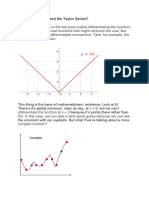
- The Taylor SeriesDocument5 pagesThe Taylor Seriessal27adamNo ratings yet
- Completing The Square WorksheetDocument6 pagesCompleting The Square Worksheetezmoreldo100% (1)
- Lec 31Document29 pagesLec 31Anonymous naEAR9adNo ratings yet
- Limits and ContinuityDocument19 pagesLimits and ContinuityTanmoy ChakrabortyNo ratings yet
- Introduction To Finite Element Method Dr. R. Krishnakumar Department of Mechanical Engineering Indian Institute of Technology, Madras Lecture - 14Document21 pagesIntroduction To Finite Element Method Dr. R. Krishnakumar Department of Mechanical Engineering Indian Institute of Technology, Madras Lecture - 14mahendranNo ratings yet
- Rational ExpressionsDocument28 pagesRational ExpressionsrinafuentesNo ratings yet
- Calculation of FunctionsDocument8 pagesCalculation of FunctionsMonica FlowersNo ratings yet
- 1 What Is An Exact Answer?: Equations. Whether Finding An Output Value of A Function or A Solution ToDocument3 pages1 What Is An Exact Answer?: Equations. Whether Finding An Output Value of A Function or A Solution ToTally TengNo ratings yet
- Lecture Notes: Abstract Algebra: Rajat MittalDocument47 pagesLecture Notes: Abstract Algebra: Rajat MittalMizanur RahmanNo ratings yet
- Rajat Mittal Abstract Algebra PDFDocument47 pagesRajat Mittal Abstract Algebra PDFAnonymous RVVCJlDU6100% (1)
- Integration by PartsDocument24 pagesIntegration by Partsalokesh1982No ratings yet
- IntegralsDocument90 pagesIntegralsJuly LumantasNo ratings yet
- Orientation Course in Mathematics: Santosh Kumar Bhal Assistant ProfessorDocument80 pagesOrientation Course in Mathematics: Santosh Kumar Bhal Assistant ProfessorAnkita PradhanNo ratings yet
- MA 109 College Algebra Chapter 1 PDFDocument20 pagesMA 109 College Algebra Chapter 1 PDFr22_22No ratings yet
- Differential EquationsDocument1 pageDifferential Equationsjushmo024No ratings yet
- CalcI AreaProblemDocument12 pagesCalcI AreaProblemJose V. Chunga MunaycoNo ratings yet
- Integration MethodsDocument30 pagesIntegration MethodsAya AbdelsanadNo ratings yet
- Section: The LimitDocument12 pagesSection: The Limitlady chaseNo ratings yet