Formula 4 : Fourier Series

Even Function
1) symmetric about y-axis
2) ) ( ) ( x f x f =
3) Eg :
x y cos = ,
2
x y =
4)
}

t
t
dx x f ) ( =
}
t
0
) ( 2 dx x f
5)
}

L
L
dx x f ) ( =
}
L
dx x f
0
) ( 2

Odd Function
1) symmetric about origin
2) ) ( ) ( x f x f =
3) Eg:
x y sin = ,
3
x y = , x y =
4)
}

t
t
dx x f ) ( = 0
5)
}

L
L
dx x f ) ( = 0

Fourier Series on Interval ) , ( t t
{ }

=
+ + =
1
sin cos
2
) (
n
n n
o
nx b nx a
a
x f
1
( )
o
a f x dx
t
t
t

=
}

1
( ) cos
n
a f x nx dx
t
t
t

=
}

1
( )sin
n
b f x nx dx
t
t
t

=
}


If f is even function, then
{ }

=
+ =
1
cos
2
) (
n
n
o
nx a
a
x f
}
=
t
t
0
) (
2
dx x f a
o

}
=
t
t
0
cos ) (
2
dx nx x f a
n


If f is odd function
{ }

=
=
1
sin ) (
n
n
nx b x f
}
=
t
t
0
sin ) (
2
dx nx x f b
n

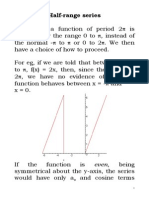
Half Range Series: a series that is
defined on the interval ) , 0 ( t but has
period 2t,

Half Range Cosine Series
{ }

=
+ =
1
cos
2
) (
n
n
o
nx a
a
x f
}
=
t
t
0
) (
2
dx x f a
o

}
=
t
t
0
cos ) (
2
dx nx x f a
n


Half Range Sine Series
{ }

=
=
1
sin ) (
n
n
nx b x f
}
=
t
t
0
sin ) (
2
dx nx x f b
n