Professional Documents
Culture Documents
Assignment 2 Answer
Assignment 2 Answer
Uploaded by
Muhammad ZH SarOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Assignment 2 Answer
Assignment 2 Answer
Uploaded by
Muhammad ZH SarCopyright:
Available Formats
SMJM2043 ASSIGNMENT 2 Odd Number Groups
Note: Marking Scheme: M1= 1 mark for method, A1= 1 mark for answer
2-127. a) P( A B )= 22/100, P(A) = 30/100, P(B) = 77/100, M1
Then P( A B ) P(A)P(B), therefore, A and B are not independent. A1
b) P(B|A) = P(A B)/P(A)\ M1
= (22/100)/(30/100) = 0.733 A1
2-133. (a) The probability that one technician obtains equivalence at 100 mL is 0.1.
So the probability that both technicians obtain equivalence at 100 mL is
2
0.1 0.01 . A1
(b) The probability that one technician obtains equivalence between 98 and 104 mL is 0.7.
M1
So the probability that both technicians obtain equivalence between 98 and 104 mL is
49 . 0 7 . 0
2
. A1
(c) The probability that the average volume at equivalence from the technician is 100 mL is
09 . 0 ) 1 . 0 ( 9
2
. A1
2-139. P(A) = 4329/22252 = 0.1945, P(B) = 953/22252 = 0.0428,
P(A B) = 242/22252 = 0.0109 M1
Because P(A)*P(B) = (0.1945)(0.0428) = 0.0083 0.0109 = P(A B), A and B are not
independent. A1
2-147. Let G denote a product that received a good review. Let H, M, and P denote products that were
high, moderate, and poor performers, respectively.
a)
( ) ( ) ( ) ( ) ( ) ( ) ( )
0.95(0.40) 0.60(0.35) 0.10(0.25)
0.615
P G P G H P H P G M P M P G P P P
M1 A1
b) Using the result from part a.,
( ) ( )
( )
( )
0.95(0.40)
0.618
0.615
P G H P H
P H G
P G
M1 A1
c)
( ' ) ( )
( ')
( ')
0.05(0.40)
0.052
1 0.615
P G H P H
P H G
P G
M1 A1
2-148. a) P(D)=P(D|G)P(G)+P(D|G)P(G) M1
=(.005)(.991)+(.99)(.009)=0.013865 A1
b) P(G|D)=P(GD)/P(D)=P(D|G)P(G)/P(D) M1
=(.995)(.991)/(1-.013865)=0.9999 A1
You might also like
- Ch02 SolutionDocument38 pagesCh02 SolutionSharif M Mizanur Rahman90% (10)
- ch04 PDFDocument89 pagesch04 PDFNadya Azzan67% (3)
- 3.4. A Computer ANOVA Output Is Shown Below. Fill in The Blanks. You May Give Bounds On The P-Value.Document35 pages3.4. A Computer ANOVA Output Is Shown Below. Fill in The Blanks. You May Give Bounds On The P-Value.Kamiran MuhammadNo ratings yet
- Homework 2 Solutions: CS3130: Probability and Statistics For EngineersDocument2 pagesHomework 2 Solutions: CS3130: Probability and Statistics For EngineersKaleb SchmidtNo ratings yet
- Project Guidance For Research Design v1Document24 pagesProject Guidance For Research Design v1Muhammad ZH SarNo ratings yet
- Exercises SolutionsDocument67 pagesExercises SolutionsMichał Augustyniak100% (2)
- BTH780 Reliability Engineering Lecture Material#3Document173 pagesBTH780 Reliability Engineering Lecture Material#3Neuky ElsNo ratings yet
- Solutions For Exercises in Chapter 2Document3 pagesSolutions For Exercises in Chapter 2Felipe DiazNo ratings yet
- GATE Chemical Engineering 2007Document31 pagesGATE Chemical Engineering 2007Gurunath EpiliNo ratings yet
- StatisticsDocument11 pagesStatisticsVedha VetriselvanNo ratings yet
- Probability and Random Variables: Solutions To Problems 2021Document16 pagesProbability and Random Variables: Solutions To Problems 2021PALLAV GUPTANo ratings yet
- Solution Manual StatsDocument589 pagesSolution Manual StatsShaundiLil67% (3)
- MGS3100 Sample Exam Questions #3Document6 pagesMGS3100 Sample Exam Questions #3api-25888404No ratings yet
- (Probability and Linear Programming) : Hints/Solutions For M1210Document6 pages(Probability and Linear Programming) : Hints/Solutions For M1210Sivakumar NatarajanNo ratings yet
- Answer All Questions in This SectionDocument6 pagesAnswer All Questions in This SectionSK100% (1)
- Design and Analysis of ExperimentsDocument12 pagesDesign and Analysis of Experimentsnilesh291No ratings yet
- PS1 Solution (8e)Document3 pagesPS1 Solution (8e)LUCKYTODAY IFEELNo ratings yet
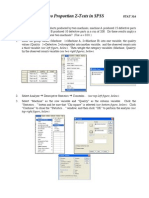
- Two Proportion Z-Tests in SPSS: Top-Right Figure, Below)Document2 pagesTwo Proportion Z-Tests in SPSS: Top-Right Figure, Below)Đồng NguyễnNo ratings yet
- MPM 3 Sample ADocument3 pagesMPM 3 Sample AmakoplNo ratings yet
- IT1005 Lab 06 Answer Book: Problem 1Document4 pagesIT1005 Lab 06 Answer Book: Problem 1hideto290No ratings yet
- 2Document4 pages2SagarNo ratings yet
- Jan 2021 S2 MSDocument10 pagesJan 2021 S2 MSGary ChowNo ratings yet
- Assignment 1 Eco204 Sec 2 MD Nafis 2018-1-10-278Document11 pagesAssignment 1 Eco204 Sec 2 MD Nafis 2018-1-10-278Md NafisNo ratings yet
- Answer Key Homework 8 (Due Date: April 8, 2005, Friday in Class)Document3 pagesAnswer Key Homework 8 (Due Date: April 8, 2005, Friday in Class)Rain MalabananNo ratings yet
- Feedback Amplifier AssignmentDocument2 pagesFeedback Amplifier AssignmentShreyaank RaoNo ratings yet
- Name: Hesham Al-Khalawi ID: 201783050 Section: 05 Q8 AnswerDocument6 pagesName: Hesham Al-Khalawi ID: 201783050 Section: 05 Q8 AnswerH.K.No ratings yet
- Latihan Soal M11 - Kelompok 02 Kelas BDocument9 pagesLatihan Soal M11 - Kelompok 02 Kelas BDanindra Meitriandi CaesarioNo ratings yet
- Solution HW4Document10 pagesSolution HW4Daniel Zednanreh ZeugnimodNo ratings yet
- hw2 Solutions STAT430Document10 pageshw2 Solutions STAT430Sebastian GonzalezNo ratings yet
- Tolerance Analysis 09.04.03Document26 pagesTolerance Analysis 09.04.03maddy_scribdNo ratings yet
- Teorema Del Limite CentralDocument14 pagesTeorema Del Limite CentralmodestorosNo ratings yet
- Control Systems: V I A VDocument6 pagesControl Systems: V I A VIgor OliveiraNo ratings yet
- AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document5 pagesAJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- Statistics For Business Set Theory and Probability LaboratoryDocument7 pagesStatistics For Business Set Theory and Probability Laboratoryangelica.r.altamirano1992No ratings yet
- Business Statistics Topic 3 Tutorial Solutions (Q1-Q10)Document4 pagesBusiness Statistics Topic 3 Tutorial Solutions (Q1-Q10)Beryl ChanNo ratings yet
- 610 HW3Document4 pages610 HW3anchtigerNo ratings yet
- 2023 3 Kel State ADocument6 pages2023 3 Kel State AChin Ling ChiengNo ratings yet
- Ex ContinuousprobDocument19 pagesEx Continuousprobabed311No ratings yet
- ListaEstatisticaProbabilidade 1Document5 pagesListaEstatisticaProbabilidade 1Adrielly IslyNo ratings yet
- HW 4 A 1Document11 pagesHW 4 A 1draconnoxNo ratings yet
- Stat Assign 3 SolDocument3 pagesStat Assign 3 SolErum Shaikh0% (1)
- 16 CH11a-isbe11Document135 pages16 CH11a-isbe11tomNo ratings yet
- Assignment 1Document11 pagesAssignment 1sherianwedderburnNo ratings yet
- A. P (A B) P (A) + P (B) : To Answer Questions 6 To 21 Use The Table Standard Normal Distribution As FollowsDocument15 pagesA. P (A B) P (A) + P (B) : To Answer Questions 6 To 21 Use The Table Standard Normal Distribution As Followsdidik1991No ratings yet
- Bayes TheoremDocument22 pagesBayes TheoremRISHAB NANGIANo ratings yet
- Chapter #19 Solutions - Engineering Economy, 7 TH Editionleland Blank and Anthony TarquinDocument15 pagesChapter #19 Solutions - Engineering Economy, 7 TH Editionleland Blank and Anthony TarquinMusa'bNo ratings yet
- Probability - Homework Week 2Document8 pagesProbability - Homework Week 2uses privateNo ratings yet
- Two Proportion Z-Tests in SPSS: Top-Right Figure, Below)Document2 pagesTwo Proportion Z-Tests in SPSS: Top-Right Figure, Below)Amado SaavedraNo ratings yet
- Newbold Ism 04 PDFDocument19 pagesNewbold Ism 04 PDFIrakli MaisuradzeNo ratings yet
- WJEC S1 Jan 2007 Marking SchemeDocument4 pagesWJEC S1 Jan 2007 Marking Schemedela2No ratings yet
- Amc8 V5Document181 pagesAmc8 V5Shuai ChenNo ratings yet
- Week 12 Tutorial 11 Review Questions and SolutionsDocument17 pagesWeek 12 Tutorial 11 Review Questions and SolutionsĐặng Thịnh NguyễnNo ratings yet
- CH 3 SolutionsDocument10 pagesCH 3 SolutionsAndy LeeNo ratings yet
- PS Solutions Chapter 14Document5 pagesPS Solutions Chapter 14Michael SubrotoNo ratings yet
- SPC: Statistical Process ControlDocument53 pagesSPC: Statistical Process ControlSaoloan NaiborhuNo ratings yet
- The Electromagnetic Field EquationsDocument2 pagesThe Electromagnetic Field EquationsMuhammad ZH SarNo ratings yet
- Chemistry Form 4 - Acid and Base - PPTDocument68 pagesChemistry Form 4 - Acid and Base - PPTMuhammad ZH SarNo ratings yet
- Nota Chemistry SPMDocument3 pagesNota Chemistry SPMacila88% (8)