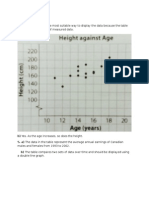
5.

5
1. a) Histogram is the most appropriate type of graph because data are grouped in
intervals.

b) Bar graph is the most appropriate type of graph because data represent numbers
of different items.

2. a) Hours per week that elementary school students participate in sports.

b)

c) From the data and the graphs, we can infer that most boys and girls spend 3-5 h
per week participating in sports. Also, more boys than girls spend 12-14 h per week
participating in sports.

4. a)

b) Median = 114 there were equal number of days when there were fewer than
114 ice cream bars were sold and when more than 114 ice cream bars were sold
Mode = 125 There were more days when 125 ice cream bars were sold compared
to any other day with a different number of ice cream bars.
c)

d) You can identify each piece of data from the stem-and-leaf plot. In the frequency
table, you know only how many pieces of data are in each interval. You do not know
the values of the data.

e)

f) On most days in July, 100 or more ice cream bars were sold at the community
centre.
5. a)i)

ii) From this graph, it is easy to see that more jeans are less than $100 than those
priced at $100 or more.
iii) We can estimate the median but not the mode (because it only shows the
intervals in which the data lie). If we add the heights of the bars we would get 44.
This tells us that there are 44 pieces of data. The median is the mean of the 22 nd
and 23rd pieces of data. These pieces of data fall in the 60-80 interval. I would
estimate the median to be about $65.

b)i)

ii) It is easy to see that most books are from 10-49 mm thick.
iii) We can estimate the median but not the mode (because it only shows the
intervals in which the data lie). If we add the heights of the bars we would get 50.
This tells us that there are 50 pieces of data. The median is the mean of the 25 th
and 26th pieces of data. These pieces of data fall in the 30-39 interval. I would
estimate the median to be about 37 mm.