Professional Documents
Culture Documents
Fluids - Lecture 16 Notes: Shock Losses
Fluids - Lecture 16 Notes: Shock Losses
Uploaded by
Mahmoud NasrOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Fluids - Lecture 16 Notes: Shock Losses
Fluids - Lecture 16 Notes: Shock Losses
Uploaded by
Mahmoud NasrCopyright:
Available Formats
Fluids Lecture 16 Notes
1. Shock Losses 2. Compressible-Flow Pitot Tube Reading: Anderson 8.6, 8.7
Shock Losses
Stagnation pressure jump relation The stagnation pressure ratio across the shock is po2 p2 = po1 p1 1+ 1+
1 2 M2 2 1 2 M1 2 /(1)
(1)
where both p2 /p1 and M2 are functions of the upstream Mach number M1 , as derived previously. The gures show the po2 /po1 ratio, with the second gure showing an expanded scale near M1 1.
1.0
0.9
0.8
0.7
po2/po1
0.6
0.5
0.4
0.3
0.2
0.1
0.0 1.0
1.2
1.4
1.6
1.8
2.0 M1
2.2
2.4
2.6
2.8
3.0
1.00
0.99
0.98
0.97
0.96
0.95
0.94
0.93 1.0
po2/po1
1.05
1.1
1.15
1.2
1.25 M1
1.3
1.35
1.4
1.45
1.5
The fractional shock total-pressure loss 1 po2 /po1 is seen to be small for M1 close to unity, but increases rapidly for higher Mach numbers. Minimizing this loss is of great practical importance, since it cuts directly into the performance of supersonic air-breathing engines. 1
Compressible-Flow Pitot Tube
Subsonic pitot tube A pitot tube in subsonic ow measures the local total pressure po . Together with a measurement of the static pressure p, the Mach number can be computed from the po /p ratio relation. po = p M2
M, p
1+
1 2 M 2
/(1)
2 po = 1 p
(1)/
(2)
po
po p
p
s
po
po
The pitot-static combination therefore constitutes a Mach meter With M 2 known, we can . then also determine the dynamic pressure. 1 po V 2 = pM 2 = p 2 2 1 p The velocity can be determined from V 2 = a2 M 2 = a2 M 2 o 1 + 1 M 2 2
(1)/
(3)
but this requires knowing either the static speed of sound a, or the stagnation speed of sound ao . The latter can be obtained by measuring the stagnation temperature at the tip of the pitot probe. Supersonic pitot tube A pitot probe in a supersonic stream will have a bow shock ahead of it. This complicates the ow measurement, since the bow shock will cause a drop in the total pressure, from po1 to po2 , the latter being sensed by the pitot port. Its useful to note that the shock will also cause a drop in o , but ho will not change. The pressures and Mach number immediately behind the shock are related by po2 = p2 1+ 1 2 M2 2 2
/(1)
ho1
h1 o
1
h2
ho2
1 M1 , p1 po1
po2
p2
p1
po2
bow shock
po2
In addition, we also have M2 and p2 /p1 as functions of M1 from the earlier normal-shock analysis. Combining these produces the relation between the po2 measured by the pitot probe, the static p1 , and the required ow Mach number M1 . After some manipulation, the result is the Rayleigh Pitot tube formula . po p2 po2 = 2 = p1 p2 p1
2 ( +1)2 M1 2 4M1 2( 1) /(1) 2 1 + 2M1 +1
(4)
The gure shows po2 /p1 versus M1 , compared with the isentropic ratio po1 /p1 . po1 = p1 1 + 1 2 M1 2
/(1)
(5)
Only the latter is plotted for M1 < 1, where there is no bow shock, and so equation (4) does not apply. The eect of the pitot bow shocks total pressure loss, indicated by the dierence po1 po2 , becomes substantial at larger Mach numbers. Ideally, we would like to have the pitot formula (4) give M1 as an explicit function of the pitot/static pressure ratio po2 /p1 . However, this is not possible due to its complexity, so a numerical solution is required. The function is also readily available in table form.
6.0 5.5 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0 0.0 0.2 0.4 0.6 0.8 1.0 M1 1.2 1.4 1.6 1.8 2.0 po2/p1 po1/p1
You might also like
- Gas Dynamics Equation SheetDocument5 pagesGas Dynamics Equation SheetMicha VardyNo ratings yet
- Double WedgeDocument9 pagesDouble WedgeKarthick MurugesanNo ratings yet
- Module II Solved Problems in Nozzle and DiffuserDocument13 pagesModule II Solved Problems in Nozzle and DiffuserSakthivel Munirajan100% (2)
- Sluice Gate (Fluid Mechanics)Document3 pagesSluice Gate (Fluid Mechanics)Aiko Fero33% (3)
- Mach NumberDocument54 pagesMach NumberMohammed Al-samarraeNo ratings yet
- Choked FlowDocument3 pagesChoked FlowyowmunNo ratings yet
- dm dt ∀ ρ γ P ρ dP dt: ρ ρ P P ρ P γ+1 PDocument4 pagesdm dt ∀ ρ γ P ρ dP dt: ρ ρ P P ρ P γ+1 PJeffery WilliamsNo ratings yet
- M M P P: Chapter 5 Solutions Problem 5.1Document21 pagesM M P P: Chapter 5 Solutions Problem 5.1Mansi ShahNo ratings yet
- Two Dimensional Oblique Shocks Expansion FlowsDocument18 pagesTwo Dimensional Oblique Shocks Expansion FlowsSakib RajiunNo ratings yet
- Spin and Intensity Rules: SupplementDocument2 pagesSpin and Intensity Rules: SupplementGilberto RuizNo ratings yet
- Chapter 11: Steady Waves in Compressible FlowDocument22 pagesChapter 11: Steady Waves in Compressible FlowDeez34PNo ratings yet
- Lec 8 - Compressible Duct Flow With FrictionDocument23 pagesLec 8 - Compressible Duct Flow With FrictionRicky LuznyNo ratings yet
- Normal Shock Waves PDFDocument4 pagesNormal Shock Waves PDFVikas SandhuNo ratings yet
- Supersonic Flow Over A Wedge (Oblique Shock Problem)Document29 pagesSupersonic Flow Over A Wedge (Oblique Shock Problem)sameer100% (2)
- Triple-Channel Macro-And Micro-Diversity Over Shadowed Fading Channels Using Compound ModelDocument6 pagesTriple-Channel Macro-And Micro-Diversity Over Shadowed Fading Channels Using Compound ModelPopovićJZoranNo ratings yet
- Applications Mach NumberDocument3 pagesApplications Mach NumberSaad Al HelyNo ratings yet
- Applications Mach NumberDocument3 pagesApplications Mach NumberAnonymous 6SivdzjNo ratings yet
- Fluids - Lecture 15 Notes: Mach Number RelationsDocument4 pagesFluids - Lecture 15 Notes: Mach Number RelationsPracheeNo ratings yet
- S.L. Dixon and Cesare Hall (Auth.) - Fluid Mechanics and Thermodynamics of Turbomachinery-Butterworth-HeinDocument3 pagesS.L. Dixon and Cesare Hall (Auth.) - Fluid Mechanics and Thermodynamics of Turbomachinery-Butterworth-Heinsamarsinghai26No ratings yet
- Semiconductor LasersDocument17 pagesSemiconductor LasersParisa KhosraviNo ratings yet
- ObliqueshockDocument5 pagesObliqueshockMike GlaswellNo ratings yet
- Theoretic Base For Prandtl: Incompressible FlowDocument5 pagesTheoretic Base For Prandtl: Incompressible FlowConstantin MihaiNo ratings yet
- Me 1303 Gas Dynamics and Jet Propulsion: Presented byDocument10 pagesMe 1303 Gas Dynamics and Jet Propulsion: Presented byArul SankaranNo ratings yet
- M2 L 5Document6 pagesM2 L 5Arun YogaNo ratings yet
- Frequency Components: Harmonic Modeling of Periodic WaveformsDocument4 pagesFrequency Components: Harmonic Modeling of Periodic WaveformsMohammed AnsafNo ratings yet
- Solutions To Peskin & Schroeder: 1 Weak-Interaction Contributions To The Muon G 2Document10 pagesSolutions To Peskin & Schroeder: 1 Weak-Interaction Contributions To The Muon G 2Andres PalchucanNo ratings yet
- 1D Gas Dynamic FlowsDocument3 pages1D Gas Dynamic FlowsStefano BattarraNo ratings yet
- Chapter 3Document15 pagesChapter 3Bheemesh GudelliNo ratings yet
- Hard Pion and Prompt PhotonDocument31 pagesHard Pion and Prompt Photonhaddig8No ratings yet
- Fast Fourier TransformDocument37 pagesFast Fourier TransformAnelia NefiruNo ratings yet
- Directional Magnetoelectric Effects in Mnwo4: Magnetic Sources of The Electric PolarizationDocument7 pagesDirectional Magnetoelectric Effects in Mnwo4: Magnetic Sources of The Electric PolarizationBhabani Sankar SwainNo ratings yet
- Lecture No.12 Compressible FluiddocxDocument15 pagesLecture No.12 Compressible Fluiddocxseif elsaieNo ratings yet
- Correspondence Primary: FOR LOS CaliforniaDocument5 pagesCorrespondence Primary: FOR LOS CaliforniaSaraNo ratings yet
- Pipeline Engineering: Fluid FlowDocument32 pagesPipeline Engineering: Fluid Flowzahidwahla1No ratings yet
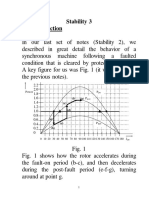
- EE457-Stability 3Document15 pagesEE457-Stability 3Fengxing ZhuNo ratings yet
- Fourth Exam Fourier - NotesDocument5 pagesFourth Exam Fourier - NotesGil Kenneth San MiguelNo ratings yet
- Homework of Bernoulli EqDocument8 pagesHomework of Bernoulli EqSinggih OktavianNo ratings yet
- Russian FET CompressorDocument15 pagesRussian FET CompressorcrackintheshatNo ratings yet
- Coupled - Pendulum ManualDocument8 pagesCoupled - Pendulum ManualmokshumohitNo ratings yet
- Porting Analysis Directed To Shotguns: 1 The Flow Through PortsDocument13 pagesPorting Analysis Directed To Shotguns: 1 The Flow Through PortsjwfosteNo ratings yet
- Coupled Pendula With "Measure-Dynamics": P2132580 Phywe Systeme GMBH & Co. KG © All Rights Reserved 1Document15 pagesCoupled Pendula With "Measure-Dynamics": P2132580 Phywe Systeme GMBH & Co. KG © All Rights Reserved 1Barthélemy HoubenNo ratings yet
- FET Compressors PDFDocument12 pagesFET Compressors PDFΛιθοξόος ΈλληνNo ratings yet
- GasDynamic SubroutinesDocument4 pagesGasDynamic SubroutinesYasser BahaaNo ratings yet
- Problem No. 1: 1 Find The Total Elongation, Stress, Strain For Stepped Bar, WhenDocument3 pagesProblem No. 1: 1 Find The Total Elongation, Stress, Strain For Stepped Bar, WhenAjay VasanthNo ratings yet
- HW 6 SolutionsDocument11 pagesHW 6 Solutionskaren dejoNo ratings yet
- Thermodynamic Model of The Loss Factor Applied To Steam TurbinesDocument7 pagesThermodynamic Model of The Loss Factor Applied To Steam TurbinesHatem Abdelrahman100% (1)
- Converging Diverging NozzleDocument6 pagesConverging Diverging NozzleShivam WankhedeNo ratings yet
- Fiber in Ducts: NPTEL IIT Kharagpur: Prof. K.P. Sinhamahapatra, Dept. of Aerospace EngineeringDocument6 pagesFiber in Ducts: NPTEL IIT Kharagpur: Prof. K.P. Sinhamahapatra, Dept. of Aerospace EngineeringArun YogaNo ratings yet
- Experiment 4 Pendulum Oscillation With PC Interface: Principle and TaskDocument5 pagesExperiment 4 Pendulum Oscillation With PC Interface: Principle and TaskNguyễn Đức MạnhNo ratings yet
- Amplitude Modulation TutorialDocument18 pagesAmplitude Modulation TutorialPavan PrakashNo ratings yet
- حل امنیتDocument12 pagesحل امنیتErfan Gholami Qadikola50% (2)
- Boiler StressDocument8 pagesBoiler Stressmohamed ramadanNo ratings yet
- Exercises in Electronics: Operational Amplifier CircuitsFrom EverandExercises in Electronics: Operational Amplifier CircuitsRating: 3 out of 5 stars3/5 (1)
- VLF Radio Engineering: International Series of Monographs in Electromagnetic WavesFrom EverandVLF Radio Engineering: International Series of Monographs in Electromagnetic WavesNo ratings yet
- Tables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiFrom EverandTables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiNo ratings yet
- Analysis and Design of Multicell DC/DC Converters Using Vectorized ModelsFrom EverandAnalysis and Design of Multicell DC/DC Converters Using Vectorized ModelsNo ratings yet
- Fundamentals of Electronics 1: Electronic Components and Elementary FunctionsFrom EverandFundamentals of Electronics 1: Electronic Components and Elementary FunctionsNo ratings yet
- Method of Moments for 2D Scattering Problems: Basic Concepts and ApplicationsFrom EverandMethod of Moments for 2D Scattering Problems: Basic Concepts and ApplicationsNo ratings yet
- Euro 5 Diesel: Use: As Fuel For Diesel EnginesDocument2 pagesEuro 5 Diesel: Use: As Fuel For Diesel EnginesMahmoud NasrNo ratings yet
- Distillate HydrocrackingDocument23 pagesDistillate HydrocrackingMahmoud Nasr100% (1)
- List of Contents: Special Issue 2013 Danckwerts Special Issue On Molecular Modelling in Chemical EngineeringDocument2 pagesList of Contents: Special Issue 2013 Danckwerts Special Issue On Molecular Modelling in Chemical EngineeringMahmoud NasrNo ratings yet
- Darcy-Weisbach Equation For Head Loss in A Pipe: ParametersDocument2 pagesDarcy-Weisbach Equation For Head Loss in A Pipe: ParametersMahmoud NasrNo ratings yet
- Column SizingDocument16 pagesColumn SizingSyed Muzamil Ahmed100% (9)
- A B M A M A: 2010 CH - 2 StaticsDocument5 pagesA B M A M A: 2010 CH - 2 StaticsMahmoud NasrNo ratings yet
- Feed Specification: Components Mol - WT Kmol/h C1 C2 C3 Ic4 nC4 Ic5 nC5 C6 C7 C8 C9 C10 N2 H2S CO2 609.83Document2 pagesFeed Specification: Components Mol - WT Kmol/h C1 C2 C3 Ic4 nC4 Ic5 nC5 C6 C7 C8 C9 C10 N2 H2S CO2 609.83Mahmoud NasrNo ratings yet
- Calculate Friction FactorDocument1 pageCalculate Friction FactorMahmoud NasrNo ratings yet
- Tuition Fees: For Programmes Commencing 2013-2014Document2 pagesTuition Fees: For Programmes Commencing 2013-2014Mahmoud NasrNo ratings yet
- Electrical Submersible PumpDocument24 pagesElectrical Submersible PumpJorge Mártires100% (3)
- 3G4 Distillation CalculationsDocument22 pages3G4 Distillation CalculationsMahmoud Nasr0% (1)
- What Is RheologyDocument6 pagesWhat Is RheologyMahmoud NasrNo ratings yet