ECE 4332 Homework 2

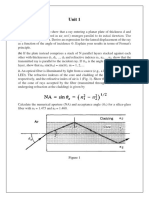
1. Derive that the complex amplitude of the double convex lens shown in the image below with focal length ( )( ). Hint: we derived an plano convex lens in class.

2. Show that when a plane wave is transmitted through a thin lens of focal length f in the direction parallel to the optical axis of the lens, its converted into a paraboloid wave (the Fresnel approximation of a spherical wave) centered about a point at a distance f from the lens.

3. A spherical wave is reflected from a planar mirror sufficiently far from the wave origin so that the Fresnel approximation is satisfied. By regarding the spherical wave locally as a plane wave with slowly varying direction, use the law of reflection of plane wave to determine the nature of the reflected wave. 4. Consider a thin transparent plate whose thickness d(x,y) is a square (instead of a sinusoidal) periodic function of x of period =. Show that the angle between the diffracted waves is still given by = /. If a plane wave is incident in a direction normal to the grating, determine the amplitude of the different diffracted plane waves. 5. Show that a pulsed spherical wave has a complex wavefunction of the form U(r,t) = (1/r)a(t-r/c) where a(t) is an arbitrary function. An ultrashort optical pulse has a complex wavefunction with a central frequency corresponding to a wavelength 0 = 585nm and a Gaussian envelope of rms width 1 = 6fs. How many cycles are contained within the pulse width? If the pulse propagates in free space as a spherical wave initiated at the origin at t = 0, describe the spatial distribution of the intensity as a function of the radial distance at time t = 1ps.