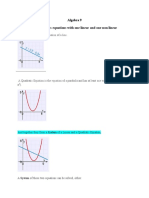
De Moivre's Theorem

De Moivre's Theorem
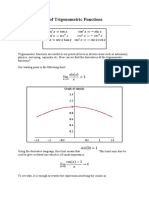
In mathematics, de Moivre's formula (a.k.a. De Moivre's theorem and De Moivre's identity), named after Abraham de Moivre, states that for any complex number (and, in particular, for any real number) x and integer n it holds that ( cos x + isin x )n = cos(nx) + isin(nx). While the formula was named after De Moivre, he never explicitly stated it in his works.The formula is important because it connects complex numbers (i stands for the imaginary unit (i2 = 1.)) and trigonometry. The expression cos x + i sin x is sometimes abbreviated to cis x. By expanding the left hand side and then comparing the real and imaginary parts under the assumption that x is real, it is possible to derive useful expressions for cos (nx) and sin (nx) in terms of cos x and sin x. Furthermore, one can use a generalization of this formula to find explicit expressions for the nth roots of unity, that is, complex numbers z such that zn = 1. Failure for non-integer powers :- De Moivre's formula does not, in general, hold for non-integer powers. Non-integer powers of a complex number can have many different values, see failure of power and logarithm identities. However there is a generalization that the right hand side expression is one possible value of the power. Know More About :- Properties of Rational Number

Math.Edurite.com

Page : 1/3

The derivation of de Moivre's formula above involves a complex number to the power n. When the power is not an integer, the result is multiple-valued, for example, when n = then: For x = 0 the formula gives 1 = 1 For x = 2 the formula gives 1 = 1. Since the angles 0 and 2 are the same this would give two different values for the same expression. The values 1 and 1 are however both square roots of 1 as the generalization asserts. No such problem occurs with Euler's formula since there is no identification of different values of its exponent. Euler's formula involves a complex power of a positive real number and this always has a defined value. Formulas for cosine and sine individually ;- Being an equality of complex numbers, one necessarily has equality both of the real parts and of the imaginary parts of both members of the equation. If x, and therefore also cos x and sin x, are real numbers, then the identity of these parts can be written using binomial coefficients. This formula was given by 16th century French mathematician Franciscus Vieta: In each of these two equations, the final trigonometric function equals one or minus one or zero, thus removing half the entries in each of the sums. These equations are in fact even valid for complex values of x, because both sides are entire (that is, holomorphic on the whole complex plane) functions of x, and two such functions that coincide on the real axis necessarily coincide everywhere. Here are the concrete instances of these equations for n = 2 and n = 3, The right hand side of the formula for cos(nx) is in fact the value Tn(cos x) of the Chebyshev polynomial Tn at cos x.

Read More About :- Rational Number Properties

Math.Edurite.com

Page : 2/3

ThankYou

Math.Edurite.Com