Name: __________________________ ID#: _ _ _ _ _ _ _

Math 0290 Section 1120, Spring 2011 Exam #2: April 7

th
, 2011
Instructor: Jared Barber
Important Notes: No calculators allowed. No notes or scratch paper of any kind except the
scratch paper given by the instructor. Throughout this test, use the methods or reasoning learned
in class or in the textbook. Using alternative outside methods will not receive full credit.
Showing your work is important. Writing down the answer (with no written steps) will not gain
full credit. Even if there are only one or two steps on the way to your answer, write them down
for full credit. In addition, you do not need to simplify your answer unless explicitly requested.
Question 1: Consider the following system:
2 1 2
2 1 1
3 '
5 '
y y y
y y y
+
+
a) Rewrite the above system using vectors and a matrix, that is, in the form
y A y

'
.
b) Find a real-valued set of fundamental solutions (note: the eigenvaluesshould be complex)
Question 2: The following differential equation describes the motion of a mass-spring system:
) 2 sin( 5 5 ' 4 ' ' t y y y + +
Two homogeneous solutions are given by:
). cos( ) ( ); sin( ) (
2
2
2
1
t e t y t e t y
t
h
t
h


a) Write down an appropriate variation of parameters guess for the particular solution to the
inhomogeneous problem. Use v
1
and v
2
as your unknown/to be determined functions.
Except for v
1
and v
2
, your solution guess should be written as an explicit function of time.
DO NOT FIND v
1
OR v
2
.
y
p,variation of parameters
=
b) Find a particular solution using the method of undetermined coefficients.
c) Write down the general solution and appropriately label the transient and steady-state
terms.
y
g
=
d) Give the time constant (corresponding to the transient terms).
T
c
=
Question 3: Consider the following piecewise function:

'

<
<

t t
t e
t
t f
t
4 ) 8 2 sin(
4 2 4
2 0
) (
2
a) Rewrite this piecewise function in terms of shifted Heaviside functions of the form H(t-c)
b) Find the Laplace transform of this function
Question 4: Consider the following initial value problem:
. 1 ) 0 ( ' ; 0 ) 0 ( ; 4 2 ' ' ' + y y t y y y
a) Find the above differential equations corresponding unit impulse response function
(denote the function by e(t))
b) Write down an integral expression for the convolution e(t)*f(t) where f(t) is the right
hand side of the original differential equation. DO NOT EVALUATE the integral.
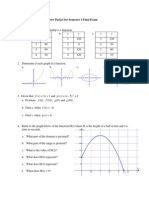
Question 5: Consider the following list of phase portraits/plots and direction fields. For each
pair of eigenvalues below, there is one and only one matching picture.
a) In the blanks provided next to the eigenvalue pairs, place the letter corresponding to the
matching picture.
b) Place arrows on the solution curves in figures B, E, and G to indicate the directions in
which the solutions are traveling, as determined by the matching eigenvalue.
i)
1
= 1+i,
2
= 1-i. ___
ii)
1
= -1,
2
= 2. ___
iii)
1
=
2
= -2. ___
iv)
1
= 3i,
2
= -3i. ___
v)
1
= -1+i,
2
= -1-i. ___
vi)
1
= 1,
2
= 3. ___
vii)
1
= -3,
2
= -1. ___
A
x ' = A x + B y
y ' = C x + D y
B = - 0.75
D = 1.25
A = - 0.25
C = - 2.25


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
D
x ' = A x + B y
y ' = C x + D y
B = - 4/3
D = 5/3
A = 7/3
C = - 2/3


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
G
x ' = A x + B y
y ' = C x + D y
B = - 1
D = - 2
A = 0
C = 2


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
B
x ' = A x + B y
y ' = C x + D y
B = 0
D = 1
A = 1
C = 0


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
E
x ' = A x + B y
y ' = C x + D y
B = - 4/3
D = 5/3
A = 7/3
C = - 2/3


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
C
x ' = A x + B y
y ' = C x + D y
B = - 1
D = - 2
A = 0
C = 2


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
F
x ' = A x + B y
y ' = C x + D y
B = - 3
D = - 3
A = 3
C = 6


-6 -4 -2 0 2 4 6
-6
-4
-2
0
2
4
6
x
y
Question 6: Find all equilibrium points of the nonlinear system:

,
_

,
_

1 2 1
2
2 2
2
1
2
1
4 '
'
y y y
y y y
y
y
Laplace Transform Table
) (t f ) (s F
1
s
1
n
t
1
!
+ n
s
n
at
e
a s
1
at n
e t 1
) (
!
+

n
a s
n
) sin(bt
2 2
b s
b
+
) cos(bt
2 2
b s
s
+
) sin(bt e
at
2 2
) ( b a s
b
+
) cos(bt e
at
2 2
) ( b a s
a s
+

) ( ' t y ) 0 ( ) ( y s sY
) ( ' ' t y ) 0 ( ' ) 0 ( ) (
2
y sy s Y s
) (t f t
n
) ( ) 1 (
) (
s F
n n

) ( ) ( c t H t H
c

s
e
cs
) ( ) ( ) ( t H t H t H
b a ab

s
e e
bs as

) ( ) ( c t H c t f ) (s F e
cs
) ( ) ( c t t
c

cs
e