EN3: Introduction to Engineering and Statics

Division of Engineering

Brown University

8 Constraint and reaction forces (and moments) at joints and contacts

Machines and structures are made up of large numbers of separate components. For example, a building consists of a steel frame that is responsible for carrying most of the weight of the building and its contents. The frame is made up of many separate beams and girders, connected to one another in some way. Similarly, an automobiles engine and transmission system contain hundreds of parts, all designed to transmit forces exerted on the engines cylinder heads to the ground. The job of a structural or mechanical engineer is to ensure that each component of a structure or machine is large enough and strong enough to bear the forces acting on it. For this purpose, we need to know how to think about the forces exerted by one part of a machine or structure on another. We do this by developing a set of rules that specify the forces associated with various types of joints and connections. 8.1 General nature of constraint forces Forces associated with joints and connections are unlike the forces weve been working with so far in this course. For all our preceding examples, (e.g. gravity, lift and drag forces, and so on) we always knew everythingabout the forces magnitude, direction, and where the force acts. The rules for forces and moments acting at joints and contacts, however, dont specify the forces completely. Usually (but not always), they will specify where the forces act; and they will specify that the forces and moments can only act along certain directions. The magnitude of the force is always unknown.

The general nature of a contact force is nicely illustrated by a familiar example you, standing on a floor. You know the floor exerts a force on you (and you must exert an equal force on the floor). If the floor is slippery, you know that the force on you acts perpendicular to the floor, but you cant make any measurements on the properties of the floor or your feet to determine what the force will be. In fact, the floor will always exert on your feet whatever force is necessary to stop them sinking through the floor. (This is generally considered to be a good thing, although there are occasions when it would be helpful to be able to break this law). We can of course deduce the magnitude of the force, by noting that since you dont sink through the floor, you are in equilibrium (according to Newtons definition anyway you may be far from equilibrium mentally). Lets say you weight 300lb (if you dont, a visit to Dunkin Donuts will help you reach this weight). Since the only forces acting on you are gravity and the contact force, the resultant of the contact force must be equal and opposite to the force of gravity to ensure that the forces on you sum to zero. The magnitude of the total contact force is therefore 300lb. In addition, the resultant of the contact force must act along a line passing through your center of gravity, to ensure that the moments on you sum to zero. From this specific example, we can draw the following general rules regarding contact and joint forces (1) All contacts and joints impose constraints on the relative motion of the touching or connected components that is to say, they allow only certain types of relative motion at the joint. (e.g. the floor imposes the constraint that your feet dont sink into it) (2) Equal and opposite forces and moments act on the two connected or contacting objects. This means that for all intents and purposes, a constraint

force acts in more than one direction at the same time. This is perhaps the most confusing feature of constraint forces. (3) The direction of the forces and moments acting on the connected objects must be consistent with the allowable relative motion at the joint (detailed explanation below) (4) The magnitude of the forces acting at a joint or contact is always unknown. It can sometimes be calculated by considering equilibrium (or for dynamic problems, the motion) of the two contacting parts (detailed explanation later). Because forces acting at joints impose constraints on motion, they are often called constraint forces. They are also called reaction forces, because the joints react to impose restrictions on the relative motion of the two contacting parts.

8.2 How to determine directions of reaction forces and moments at a joint Lets explore the meaning of statement (3) above in more detail, with some specific examples. In our discussion of your interaction with a slippery floor, we stated that the force exerted on you by the floor had to be perpendicular to the floor. How do we know this? Because, according to (3) above, forces at the contact have to be consistent with the nature of relative motion at the contact or joint. If you stand on a slippery floor, we know (1) You can slide freely in any direction parallel to the floor. That means there cant be a force acting parallel to the floor. (2) If someone were to grab hold of your head and try to spin you around, youd rotate freely; if someone were to try to tip you over, youd topple. Consequently, there cant be any moment acting on you. (3) You are prevented from sinking vertically into the floor. A force must act to prevent this. (4) You can remove your feet from the floor without any resistance. Consequently, the floor can only exert a repulsive force on you, it cant attract you.

You can use similar arguments to deduce the forces associated with any kind of joint. Each time you meet a new kind of joint, you should ask

(1) Does the connection allow the two connected solids move relative to each other? If so, what is the direction of motion? There can be no component of reaction force along the direction of relative motion. (2) Does the connection allow the two connected solids rotate relative to each other? If so, what is the axis of relative rotation? There can be no component of reaction moment parallel to the axis of relative rotation. Below, we show a list of the most common types of connection, with a brief description of the reaction forces and moments associated with each one. The components of unknown reaction force are shown using a special notation for each joint this notation will be discussed in more detail later, when we work through some examples. Standard symbols are used to denote each type of connection in engineering sketches these are shown with each joint.

8.3 Reaction Forces and Moments associated with various types of joint

Clamped, or welded joints No relative motion or rotation is possible.

Reaction forces: No relative motion is possible in any direction. Three components of reaction force must be present to prevent motion in all three directions. Reaction moments: No relative rotation is possible about any axis. Three components of moment must be present to prevent relative rotation.

2D versions of the clamped joint are shown below

Pinned joint. A pinned joint is like a door hinge, or the joint of your elbow. It allows rotation about one axis, but prevents all other relative motion.

Reaction forces: No relative motion is possible at the joint. There must be 3 components of reaction force acting to prevent motion. Reaction moments: Relative rotation is possible about one axis (perpendicular to the hinge) but is prevented about axes perpendicular to the hinge. There must be two components of moment acting at the joint.

2D pinned joints are often represented as shown in the picture below

Roller and journal bearings Bearings are used to support rotating shafts. You can buy many different kinds of bearing, which constrain the shaft in different ways. Well look at a couple of different ones. Example 1: The bearing shown below is like a pin joint: it allows rotation about one axis, but prevent rotation about the other two, and prevents all relative displacement of the shaft.

Reaction forces: No relative motion is possible at this kind of bearing. There must be 3 components of reaction force. Reaction moments: Relative rotation is allowed about one axis (parallel to the shaft), but prevented about the other two. There must be two components of reaction moment.

Example2: Some types of bearing allow the shaft both to rotate, and to slide through the bearing as shown below

Reaction forces: No relative motion is possible transverse to the shaft, but the shaft can slide freely through the bearing. There must be 2 components of reaction force. Reaction moments: Relative rotation is allowed about one axis (parallel to the shaft), but prevented about the other two. There must be two components of reaction moment.

Roller bearings dont often appear in 2D problems. When they do, they look just like a pinned joint. Swivel joint Like a pinned joint, but allows rotation about two axes. There must be 3 components of reaction force, and 1 component of reaction moment.

Reaction forces: All relative motion is prevented by the joint. There must be three components of reaction force. Reaction moments: rotation is permitted about two axes, but prevented about the third. There must be one component of reaction force present.

Swivel joints dont often appear in 2D problems. When they do, they look just like a pinned joint.

Ball and socket joint Your hip joint is a good example of a ball and socket joint. The joint prevents motion, but allows your thigh to rotate freely relative to the rest of your body.

Reaction forces: Prevents any relative motion. There must be three components of reaction force. Reaction moments. Allows free rotation about all 3 axes. No reaction moments can be present.

Ball joints dont often appear in 2D problems. When they do, they look just like a pinned joint.

Slider with pin joint Allows relative motion in one direction, and allows relative rotation about one axis

Reaction forces: Motion is prevented in two directions, but allowed in the third. There must be two components of reaction force, acting along directions of constrained motion. Reaction moments: Relative rotation is prevented about two axes, but allowed about a third. There must be two components of reaction moment.

2D slider joints are often represented as shown in the picture below

Slider with swivel joint Similar to a swivel joint, but allows motion in one direction in addition to rotation about two axes.

Reaction forces: Relative motion is prevented in two directions, but allowed in the third. There must be two components of reaction force acting to prevent motion. Reaction moments: Rotation is permitted around two axes, but prevented around the third. There must be one component of reaction moment.

In 2D, a slider with swivel looks identical to a slider with a pin joint.

8.4 Contact Forces Contacts are actually a bit more complex than our glib discussion of your interaction with a slippery floor might suggest. The nature of the forces acting at a contact depends on three things: (1) Whether the contact is lubricated, i.e. whether friction acts at the contact (2) Whether there is significant rolling resistance at the contact (3) Whether the contact is conformal, or nonconformal. A detailed discussion of friction forces will be left until later. For now, we will consider only two limiting cases (a) fully lubricated (frictionless) contacts; and (b) ideally rough (infinite friction) contacts. Rolling resistance will not be considered at all in this course.

Forces acting at frictionless nonconformal contacts

A contact is said to be nonconformal if the two objects initially touch at a point. The contact between any two convex surfaces is always non-conformal. Examples include contact between two balls, a ball and a flat surface, or contact between two non-parallel cylinders. The simplest approximation to the forces acting at a non-conformal lubricated contact states that (1) Each solid is subjected to a force at the contact point; (2) The forces between the two solids are repulsive; this requires and for both examples illustrated in the picture; (3) The direction of the forces are along the line connecting the centers of curvature of the two contacting surfaces; (4) The moments acting on each solid at the contact point are negligible.

Three rules that help to establish the direction of frictionless contact forces are: (1) When one of the two contacting surfaces is flat, the force must act perpendicular to the flat surface; (2) When two solids contact along sharp edges, the contact force must be perpendicular to both edges. (3) When two curved surfaces contact, the reaction force acts along a line joining the centers of curvature of the two objects.

Forces acting at rough (infinite friction) nonconformal contacts

A rough nonconformal contact behaves somewhat like a pinned joint. There can be no relative motion of the contacting surfaces, therefore there must be three components of reaction force acting on both contacting solids. Unlike a pin joint, however, the contact can only sustain a repulsive normal force. This means that the components of force shown in the picture must satisfy normal force is zero (eg when the two surfaces are about to separate), the tangential forces as well. . If the

The contacting solids can rotate freely relative to one another. Therefore there must be no moment acting on the contacting solids at the point of contact.

Usually the forces acting at a rough contact are represented by components acting perpendicular and parallel to the contacting surfaces, as shown in the picture above. If you do this, its easy to enforce the constraint. But if its more convenient, you can treat the contact just like a pin joint, and express the reaction forces in any arbitrary basis, as shown in the picture below.

Theres a minor disadvantage to doing this its not easy to check whether the normal force between the surface is repulsive. You can do it using vectors for the picture shown the normal force is repulsive if

Forces acting at frictionless conformal contacts A contact is said to be conformal if two objects initially contact over a finite area. Examples include contact between the face of a cube and a flat surface; contact between the flat end of a cylinder and a flat surface; or a circular pin inside a matching circular hole. Two conformal solids are actually subjected to a pressure over the area where they are in contact. Its really hard to calculate the pressure distribution (you have to model the deformation of the two contacting solids), so instead we replace the pressure by a statically equivalent force.

If the two contacting surfaces are flat, then (1) The reaction force can be modeled as a single force, with no moment (2) The force can act anywhere within the area of contact (its actual position is determined by force and moment balance) (3) The force must be perpendicular to the two surfaces (4) The force acts to repel the two solids. You can of course make really weird conformal contacts like a jigsaw connection that can completely prevent both relative translation and rotation of the contacting solids. In this case the contact behaves just like a clamped joint.

Forces acting at ideally rough (infinite friction) conformal contacts

No relative motion can occur at the contact. There must therefore be three components of force acting on each solid. The forces can act anywhere within the area of contact (its actual position is determined by force and moment balance)

The component of force acting normal to the surface must be repulsive. No relative rotation of the two solids can occur. A moment must act about an axis perpendicular to the contact to prevent relative rotation about this axis.

8.5 Example problems with reaction forces When you analyze forces in structures or machines containing joints, your first step will usually be to compute the reaction forces acting at the joints. This is not hard. The procedure is always 1. Draw a picture of the part of the machine or structure you are interested in (you might not be interested in any part of the structure. If this is the case you should draw a picture of whatever you will get paid for. Or whatever you need to pass the exam) 2. Draw arrows representing external forces and moments on the diagram. 3. Draw arrows representing the reaction forces and moments. You should follow the rules outlined above to determine what the reaction forces and moments look like. 4. Write down vector expressions for all the forces. The expressions for the reaction forces will contain variables representing unknown components of force. 5. Calculate the moment of all the forces about some convenient point 6. Write down vector expressions for all the moments. The expressions for the reaction moments will contain variables 7. Write down the equilibrium equations 8. Solve the equilibrium equations for unknown reaction forces. Well work through a series of increasingly complex examples to illustrate this procedure. We will start by solving a bunch of Mickey-Mouse problems but we will solve them as though they were complex systems. The objective is to develop a formal, systematic approach that will solve a statics problem of arbitrary complexity.

2D Mickey-mouse problem 1.

Mickey mouse of weight weight

stands on a floor as shown. The floor has

Calculate the reaction forces (as vectors) acting at A and B

Well consider Mickey and the floor together as the system of interest. We draw a picture of the system, isolated from its surroundings (disconnect all the joints, remove contacts, etc). In the picture, all the joints and connections are replaced by forces, following the rules outlined in the preceding section.

Notice how weve introduced variables to denote the unknown force components. It is sensible to use a convention that allows you to quickly identify both the position and direction associated with each variable. In this course, we will use double subscripts the first subscript shows where the force acts, the second shows its direction. Forces are always taken to be positive if they act along the positive x, y and z directions. Weve used the fact that A is a pin joint, and therefore exerts both vertical and horizontal forces; while B is a roller joint, and exerts only a vertical force. Note that we always, always draw all admissible forces on the FBD, even if we suspect that some components may turn out later to be zero. For example, its fairly clear that this force. in this example, but it would be incorrect to leave off

Well do the force balance in a table:

Force/Moment balance for floor & Mickey. Origin at A Positio Force Moment about origin n Mickey Floor

Reactio n at A Reactio n at B Total ( =0)

The equilibrium equations F=0 and M=0 for the system then show that

These are readily solved (by hand) to yield

2D Mickey Mouse problem 2 Mickey mouse of weight stands on a balcony of weight as shown. The weight of strut CB may be neglected. Calculate the reaction forces acting at A, B and C

This time we need to deal with a structure that has two parts connected by a joint (the strut BC is connected to the floor AB through a pin joint). In cases like this you have a choice of (a) treating the two parts together as a single system; or (b) considering the strut and floor as two separate systems. As an exercise, we will do both here.

A free body diagram for the balcony and strut together is shown. Note again the convention used to denote the reactions. Both A and C are pin joints, and therefore exert both horizontal and vertical forces. The force balance for this system is
Force / moment balance for balcony, Mickey and strut together (origin at A) Position Force Moment about origin Micke y Balcon

y Reacti on at A Reacti on at C

Total ( =0)

We could attempt to solve the equilibrium equations F=0 and M=0 for the system. Setting each component of force and moment to zero gives

We can partially solve these to get

but theres no way to calculate four unknowns and only 3 equations.

and

- thats because we have

This kind of thing often happens when we solve statics problems The solution is always to look for more equations. When we solve problems involving systems that contain more than one components connected by joints, we can get additional equations by considering equilibrium of each component in the system separately. This means we have to draw separate free body diagrams for the strut and the balcony, and do a force and moment balance for each one.

The picture shows free body diagrams for both components. Note the convention weve introduced to deal with the reaction force acting at B its important to use a systematic way to deal with forces exerted by one component in a system on another, or you can get hopelessly confused. The recommended procedure is 1. Label the components with numbers here the balcony is (1) and the strut is (2) 2. Denote reaction forces acting between components with the following convention. In the symbol , the superscript (1/2) denotes that the variable signifies the force exerted by component (1) on component (2) (its easy to remember that (1/2) is 1 on 2). The subscript Bx denotes that the force acts at B, and it acts in the positive x direction. 3. The forces , exerted by component (1) on component (2) are drawn in the positive x and y directions on the free body diagram for component (2). 4. The forces exerted by component (2) on component (1) are equal and opposite to , . They are therefore drawn in the negative x and y directions on the free body diagram for component (1). You need to think of the reaction force components as acting in two directions at the same time. This is confusing, but thats the way life is.

Now we can do a force and moment balance for the balcony

Force / moment balance for balcony and Mickey together (origin at A) Positio Force Moment about origin n Micke y Balcon y Reacti on at A Reacti on at B Total ( = 0)

While for the strut

Force / moment balance strut (origin at A) Position Force Moment about origin Reaction at B

Reaction at C

Total ( =0)

We can now collect together all the equations for the unknown reactions. For equilibrium of the strut/balcony together

(1. 1)

For equilibrium of the balcony

(1. 2)

For equilibrium of the strut

(1.3)

We now have 9 equations for 6 unknowns. At first sight this looks like a problem usually if there are more equations than unknowns, the system has no solution. A closer inspection shows that (1.1) is just the sum of (1.2) and (1.3), so we can use any two of (1.1), (1.2) and (1.3) to solve for the unknowns the remaining equation will be satisfied automatically.

Its not hard to solve this system of equations by hand but since were trying to develop techniques to solve more complex problems here lets do it a better way. We can have MAPLE solve the equations for us. Heres a copy of the Maple worksheet that finds a solution to (1.1) and (1.2)

so the solution is

If youre very smart, you will have noticed that we could have solved this problem far more quickly by noting that BC is a 2-force member, so the reactions at C and B must act along BC. Well discuss this and other short-cuts later. Lets summarize the general principles weve learned by working through this problem 1. When we analyze forces in a machine or structure that consists of several components connected by joints, we usually need to draw free body diagrams and perform a force and moment balance for eachcomponent. We also have the option, if we choose, to draw free body diagrams and perform force balances for groups of components, or for the whole system. 2. We developed a systematic notation to denote forces exerted by one component on another. 3. We presented a systematic procedure for setting up equations of equilibrium for each component in a system (or groups of components)

4. We found that there are several ways to get equations for unknown reaction forces we can write down equilibrium equations for each component in a system individually, or for groups of components. If we do both, the equations of equilibrium for a group of component are not new equations instead, they are combinations of the equilibrium equations for each individual component. 5. We can solve for unknown reaction forces using either equations of equilibrium for individual components in the system, or equilibrium equations for groups of components.

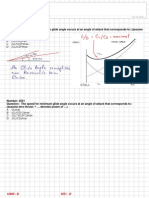
2D Mickey Mouse Problem 3 The picture shows a Mickey Mouse Mashing Machine. Calculate the mousemashing force exerted by the machine (on the mouse), in terms of the force P applied to the handle and the angle . Friction and the weight of all components may be neglected.

We have a choice of drawing free body diagrams for the lever AC, the plunger BD, for the casing, or some combination of these three. If theres any doubt about how to proceed, the safest choice is to draw free body diagrams for every individual component in the system. For this problem, it turns out to be enough to draw free body diagrams for AC and BD; theres no need to do one for the casing. Nevertheless, well show free body diagrams for all three, just as an exercise.

We also need to find a strategy to deal with the reaction forces exerted by the casing on the plunger BD. The contact prevents relative motion in the i direction, and prevents rotation. This requires a force acting in the idirection, and a moment in the k direction (treating the problem as 2D). We can place this reaction force anywhere in the contact - its really a statically equivalent resultant of the contact pressure, and statically equivalent forces can be placed anywhere. Well put the force at D. (If you like, you could work through the problem with a different choice to show that it makes no difference. Yeah, right, like youre actually going to do this.) With that preamble, here (finally) are the free body diagrams.

The free body diagrams and force labels follow the same conventions as the previous example. Two new points to note: 1. The contact at B is frictionless, and therefore only a repulsive normal force acts on the two contacting solids. The normal force exerted by member (2) (the plunger) on member (1) (the lever) is given the symbol , and its drawn on the diagram in the correct direction on both contacting members.

2. Note how the reaction at D has been labeled. The horizontal reaction exerted by member (3) on member (2) acting at D has been given the symbol . The k component of moment exerted by member (3) on member (2) has been given the symbol and its shown acting in the positive sense (counterclockwise) on member 2. We can now proceed to set up force and moment balance tables for components (1) and (2)

Force / moment balance for member (1) (lever) (origin at A) Position Force Moment about origin Appli ed force P React ion at A React ion at B

Total ( = 0)

Force / moment balance for member (2) (piston) (origin at B) Position Force Moment about origin Reaction at B Mouse

Mashing Force Reaction at D Total ( = 0)

Note how the reaction moment at D has been included in the moment column, in addition to the moment of the reaction force. We can now collect together all our equilibrium equations

(1.4 )

(1.5)

We can once again solve these on the computer

The mouse-mashing force is therefore

3D Mickey mouse problem. 3D Mickey mouse (who somehow survived the masher) of weight stands on a square floor of weight supported on bricks at 3 points. Friction and the thickness of the floor may be neglected. Calculate the reaction force exerted by the bricks on the floor as a function of the (x,y) coordinates of Mickeys position relative to A. Find regions where Mickey may safely stand without causing the floor to tip over.

3D problems may be solved using exactly the same procedure as 2D problems. We draw a free body diagram first. We take Mickey and the floor together as our system of interest

Some remarks on whats been done: 1. The weight force on the floor acts at its center of mass. We know where this is from the table provided earlier. 2. The bricks exert contact forces on the floor. The force must be repulsive and must act perpendicular to the floor, since friction has been neglected. Weve assumed the forces act at the corners of the floor. In practice the contact force could act anywhere inside the area of contact between bricks and floor, but if the bricks are much smaller than the floor it wont make any difference if we assume they act exactly at the corners. 3. The scheme used to label reaction forces is exactly the same as that introduced for 2D problems. In at A in the positive z direction. We now set up a force balance table
Force / moment balance for Mickey and Floor (origin at A) Position Force Moment about origin Gravit y on Micke y Gravit y on floor Reacti on at A Reacti on at B Reacti on at C

the subscript means the force acts

Total ( = 0)

Each component of force and each component of moment must vanish. This requires

These equations can be solved (even without Maple) for the reaction forces

Finally, we need to find safe positions for Mickey to stand. The floor will tip if any of the contact forces become negative (because contact forces can never become negative, so a static equilibrium configuration becomes impossible). Since and theres no way that or will ever become negative, but requires . The safe region is shaded green below.

8.6 Important short-cuts: reaction forces acting on two force members. Weve seen that calculating reaction forces in a machine or structure is fairly straightforward, but its very tedious process. Experienced structural and mechanical engineers take lots of short-cuts while doing preliminary design calculations. Most statics textbooks are designed to help you develop these skills usually by means of hundreds of example problems! Fortunately for you, we dont have time to do this in EN3. But there are two short cuts that are so helpful that they are worth spending some time on. A Two-force member is a component or structural member that 1. is connected only to two ball-and socket type joints (in 3D) or pin joints (in 2D). 2. has negligible weight Weve seen an example already in one of the Mickey Mouse examples its shown again in the picture to remind you. Member BC is a two-force member, because its weight is negligible, and it has only two pin joints connecting it to other members. Member AB is not a two-force member partly because its weight is not negligible, but also because Mickey exerts a force on the member.

The following rules are very helpful Only one component of reaction force acts at the joints on a 2-force member The reaction force component acts along a line connecting the two joints. Its trivial to show this if forces act on a body at only two points, and the body is in static equilibrium, then the forces have to be equal and opposite, and must also act along the same line, to ensure that both forces and moments are balanced. A generic 2 force member is shown below. Note that a 2-force member doesnt have to be straight, though it often is.

By convention, a positive reaction force is normally taken to pull at each end of the member, as shown. Equal and opposite reaction forces must act on whatever is connected to the two force member. Heres an example problem to illustrate the use of this trick. Mickey Mouse of weight W stands on a step-ladder as shown in the figure. Friction, and the weight of all components in the ladder, may be neglected. Find the reaction forces at all the joints and contacts.

We draw the free body diagrams for members ABC, CDE and BD, noting that BD is a two-force member (the other two members are not, because there are three joints on them).

Note how the reaction forces for the 2-force member (2) have been drawn the force acts in 4 different places and in 2 different directions at the same time!! Force balance tables for the steps (1) and support (3) are shown below. Theres no need to do one for the 2-force member, since force and moment balance are satisfied automatically.
Force / moment balance for steps (origin at A) Position Force Moment about origin Micke ys weight

Reacti on at A Reacti on at B Reacti on at C

Total ( = 0)

Reacti on at E Reacti on at D Reacti on at C

Force / moment balance for support (origin at E) Position Force Moment about origin 0 0

Total ( = 0)

The governing equations are thus

This looks like 6 equations for only 5 unknowns but the first and 4th equations are clearly the same, so there are actually only 5 independent equations. MAPLE has no problem finding the solution

Important short cuts: reaction forces acting on a freely rotating wheel with negligible weight Wheels are so ubiquitous that its worth developing a short-cut to deal with them. The picture shows a generic 2D wheel, mounted onto an axle with a frictionless bearing. The contact between wheel and ground is assumed to be ideally rough (infinite friction). The following trick is helpful For a freely rotating 2D wheel, there is only one component of reaction force at the contact between the ground and the wheel.

The picture below shows a free body diagram for a 2D wheel mounted on a frictionless bearing.

Since only two forces act on the wheel (the force at the axle, and the contact force), it behaves just like a 2 force member. The two forces must be equal and opposite, and must act along the same line. Moreover, the contact force must satisfy .

For a freely rotating 3D wheel, there are 2 components of reaction force acting at the contact between the wheel and ground. One component acts perpendicular to the ground; the other acts parallel to the ground and perpendicular to the plane of the wheel. The picture below shows all the forces and moments acting on a freely rotating 3D wheel. The reactions that act on the axle are also shown.

A view from in front of the wheel shows the directions of the forces and moments more clearly

The forces and moments shown are the only nonzero components of reaction force. The missing force and moment components can be shown to be zero by considering force and moment balance for the wheel. The details are left as an exercise.

Finally, a word of caution. You can only use these shortcuts if: 1. The wheels weight in negligible;

2. The wheel rotates freely (no bearing friction, and nothing driving the wheel); 3. There is only one contact point on the wheel. If any of these conditions are violated you must solve the problem by applying all the proper reaction forces at contacts and bearings, and drawing a separate free body diagram for the wheel. Example: Heres a simple example to illustrate the use of this shortcut. A bicycle travels at constant speed up a steep (20 degree) slope. The bike and rider (guess who) together have a weight W, and the position of their combined center of mass is indicated in the figure. Calculate the reaction forces acting at front and rear wheels.

A free body diagram for the bike and rider together is shown below (Mickeys legs have been amputated for clarity). The back wheel is driven, so we use the usual rules to denote contact forces acting on the back wheel (both normal and tangential forces must be present). The front wheel rolls freely, so the short-cut tells us that there is only a normal force acting at the contact point.

We now balance forces and moments, in the usual way

Position Weight Force / moment balance for bike & rider (origin at A) Force Moment about origin

Reactio n at A Reactio n at B Total ( = 0)

The governing equations are thus

which are readily solved (look Ma, no Maple!) to give

8.7 Conditions necessary to be able to calculate reaction and joint forces We saw in the preceding section that forces can not always be calculated from equilibrium equations. In general, an attempt to analyze forces acting in on a system can have three possible outcomes: 1. It is not possible to satisfy the equilibrium equations this means that the structure or component cant be in static equilibrium, and must move or collapse 2. The equilibrium equations have a unique solution. Yes! Come to Papa! 3. The equilibrium equations can be satisfied, but have many solutions. In this case we cant calculate the forces without additional information. Exactly the same can happen when you attempt to calculate reaction forces in a machine or component. Two simple examples illustrate this Example 1: The beam has weight W. Calculate the force acting at the pin joint at A.

The free body diagram is shown. You can verify for yourself that the equilibrium equations give

(taking moments about the CG). You cant satisfy all three equations So therefore the system cannot be in equilibrium (Duh). A system like this is said to be under constrained Example 2. The beam still has weight W. Calculate the reaction forces at the pin joints.

You can verify for yourself that the equilibrium equations for this system are

We clearly have a problem here there are four unknown force components, and only three equations. We can partially solve the equations to find that but theres no way to calculate a value for and opposite forces will satisfy the equations. and - any equal

A system like this one is said to be over constrained. It is sometimes possible to calculate a few force components in an over-constrained system; but often its not possible to calculate any of them without additional information. How can you tell if a system is over or under constrained? The only foolproof method is to set up the equilibrium equations and try to solve them. But there is a quick way to get a pretty good sense of whether a system is over, or under constrained. Heres what to do. 1. Count the number of separate rigid components in the system well call this number M 2. Count the unknown force components, using the rules governing force components at various joint and contact types well call this number R. Then, if the problem is 2D, use the following rules 1. If 3M>R the system is probably under-constrained (more equations than unknowns) 2. If 3M=R the system might be properly constrained 3. If 3M<R the system is over constrained (fewer equations than unknown forces) If the problem is 3D, then 4. If 6M>R the system is probably under-constrained (more equations than unknowns) 5. If 6M=R the system might be properly constrained 6. If 6M<R the system is over constrained (fewer equations than unknown forces)

8.8 Case study: analysis of torques and forces in a Hookes Joint Heres an application of the theory weve just learned. This case study is intended to show how to analyze forces in a complex 3D assembly. Once again, we dont expect you to be able to do this kind of calculation by yourself yet, Many power transmission systems contain `Constant Velocity or CV joints. In fact, if you drive a beat up car, you might well have had a call from your mechanic asking for $600 to replace your CV joints. She or he is not scamming you, these things really exist. The purpose of a CV joint is to enable a rotating shaft to bend the general nature of the device is sketched in the picture above. Shafts AB and CD need to be misaligned by a small angle , but must be connected to force them to rotate at the same angular rate. The mystery device between B and C is a CV joint. There are many designs of CV joint, and some work better than others. New ones are still being developed e.g. see http://cvcoupling.com Hookes joint is an old one it was invented by Sir Robert Hooke, who was a contemporary (and bitter enemy his nose was out of joint (queue audience laughter)) of Newton.

A real Hookes joint (from a Landrover see http://www.4wdonline.com/A.hints/Universal.html is shown in the figure above (the picture actually shows a double Hookes joint two of them connected back to back). The animation below shows how the device in action.

The picture below shows a labeled and dimensioned view of the joint.

The centerlines of shafts AB and CD are misaligned by an arbitrary angle shown. In service, the shaft AB is connected to a motor at A, which exerts a torque on the shaft. The shaft CD is connected to a load (e.g. the . An equal differential on your car) at D, and provides a driving torque and opposite torque must act on the shaft at D.

as

Our goal in this problem is 1. To predict the relationship between the angular speed of the input shaft (AB) and the output shaft (CD). In theory, they are supposed to be the same but we will discover that actually the two shafts rotate at slightly different speeds. 2. To calculate a relationship between the torque applied to the input shaft (AB) and the torque transmitted by the output shaft (CD) 3. To relate the internal forces acting at the joints P,Q,R,S to the torque. The coupling will fail if the forces at these joints get too large, so the forces must be calculated in order to determine the torque rating of the coupling. Our calculations will show how a complex 3D problem can be treated easily by a systematic use of vectors. We need to devise a way to quantify the rotation of each shaft about its axis. The two angles and are one way to do this: is the angle between OP

and the plane ABOCD, while perpendicular to ABOCD.

is the angle between OQ and the

The key to solving 3D problems is to use a convenient set of bases to describe vectors. In a complex problem like this one, it is often sensible to introduce several different Cartesian bases, which are used to represent forces acting on different parts of the system. For example, its very helpful to have basis vectors parallel and perpendicular to shaft AB in order to write down forces acting on this shaft. Similarly, its nice to have basis vectors parallel and perpendicular to shaft CD to write down forces acting on the output shaft. Of course, we cant find a basis thats parallel to both shafts, but we can go ahead and define two different bases if we want to. In this problem, we will actually find it convenient to work with three different bases, illustrated in the picture below.

The bases are chosen as follows 1. Basis {i,j,k}: Basis vector i is parallel to shaft AB; basis vector j is perpendicular to AB and lies in the plane ABOCD, basis vector k is normal to ABOCD

2. Basis basis vector basis vector

: Basis vector is parallel to shaft AB; is perpendicular to AB and lies in the plane ABOCD, is normal to ABOCD

3. Basis : basis vector is parallel to OP, basis vector is parallel to OQ and is normal to . Note that this basis rotates as the shafts revolve.

If we use many different bases in a problem, we always need to start by finding formulas relating the various basis vectors. This is straightforward. A top view of the joint shows that

Similarly, we can find the inverse formulas

Similarly, we can compute formulas for using the picture shown below

Any other relationships we may require can be found by simple vector algebra on these formulas For example, we will need formulas for - to get one, we can use . As a challenge, see if you can verify the following formulas

We can now start our calculations.

Relationship between rotational speeds of the two shafts We can immediately relate the angles and (which specify the rotation of each shaft) by noting that OQ and OP are always perpendicular, so

We can use our basis change formulas to evaluate all the dot products

so finally

This tells us that the two shafts dont quite rotate at the same speed. If shaft AB is driven to rotate at constant speed, increases linearly with time. The angle of rotation of shaft CD follows as

If the two shafts are perfectly aligned, then . If the shafts are misaligned, then lags , as shown in the graph below.

alternately leads and

This is an annoying feature of Hookes joint. The mismatch in rotation will induce vibrations, and if the shaft rotates very quickly, it will also induce large dynamic forces.

Force Analysis The force analysis is completely routine. We simply draw free body diagrams for each component in the system, and complete force balance tables as below. For defining reaction forces, we will take shaft ABO to be component (1); shaft OCD will be component (2) and the cross will be component (3). Heres a FBD for shaft ABO. The bearing at E is assumed to be capable of transmitting both moments and forces; the bearings at Q and S are assumed to be capable of transmitting only forces (you could do the analysis with reaction moments at Q and S too, but the problem is then overconstrained)

Force / moment balance for shaft ABO (origin at O) Positio Force Moment about origin n Bearing E Reactio n at Q

Reactio n at S Applied torque 0

Total ( = 0)

Heres the free body diagram and force balance for shaft OCD. The bearings are just like those on shaft ABO

Positio n Bearing F Reactio n at P Reactio n at R

Force / moment balance for shaft OCD (origin at O) Force Moment about origin

Applied torque Total ( = 0)

Finally, we deal with the little cross piece connecting the two shafts.

Positi on Reacti on at P Reacti on at Q Reacti on at R Reacti

Force / moment balance for cross OPQRS (origin at O) Force Moment about origin

on at S Total ( = 0)

We now have a set of vector force balance equations, but were not quite ready to solve them yet, because the equations for shafts ABO and OCD have a bizarre mixture of basis vectors. This is no problem, however we can just use our basis change formulas to put everything into a common basis. Before we do this, its helpful to spot that the force and moment balance equations for the cross OPQRS tell us that

We can eliminate these terms from the force and moment balance equations for the two shafts. Eliminating the and terms in the force and moment balance equations for shaft ABO, and substituting for in terms of {i,j,k} shows that

The same exercise for shaft OCD gives

Finally, were all set. We can collect a total of 18 scalar equations for 17 unknown force and moment components (this looks like a problem, but it turns out that the equations are not all independent)

You can solve these with MAPLE but actually its pretty easy to solve them by hand too. The solution is

All the other reaction force components are zero. We can simplify these expressions by using the relationship we discovered earlier between and - recall that so that

Finally, we can draw conclusions from these predictions. We notice that 1. If the shafts are perfectly aligned ( ) then the input and output torques are equal . 2. In general, the input and output torques are not equal. If the shaft is subjected to a constant driving torque then the output torque will fluctuate as . This fluctuation is generally undesirable. 3. The bearings E and F that support the two shafts must be designed to exert moments on the shaft. The magnitude of the moment is proportional to - for small misalignments, the moment will be small, but and rotates at steady speed,

if the shafts are misaligned by 45 degrees, the bearings will need to provide moments that are equal to the driving torque. This could be a serious problem. 4. The reaction forces at the joints PQRS are inversely proportional to the size of the cross piece a its in our interests to keep the joint large to minimize the reaction forces. If the shaft is perfectly aligned, the reaction forces are constant, but for they fluctuate.

Final remarks You are probably horrified by the complexity of this analysis. Is this what engineers do? You may be one of the few people who really love involved calculations like this But its more likely that you are contemplating a life of crime instead of an engineering career. Quite possibly your first crime may even involve assaulting a nearby professor. Real problems are complicated. Most real engineering calculations are like this one. Fortunately, many such calculations can now be done automatically by CAD programs. When you use a CAD program to calculate forces, you need to understand that the program is automatically setting up and solving equilibrium equations for each component in your system. You need to know that this procedure can sometimes fail (because the assembly wasnt constrained properly, or was over-constrained). You need to know enough statics to be able to check the results of the computations. But you dont actually need to wade through the horrendous calculations involved yourself. Of course, you may choose to write CAD software for a living. In that case, you not only need to know how to do this kind of calculation, but you also need to know how to make it completely general, design a user interface, and code it. Good luck!