Professional Documents
Culture Documents
SolutionsTute7 PDF
SolutionsTute7 PDF
Uploaded by
Shweta SridharOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
SolutionsTute7 PDF
SolutionsTute7 PDF
Uploaded by
Shweta SridharCopyright:
Available Formats
Tutorial Exercises: Geometric Connections
1. Geodesics in the Isotropic Mercator Projection When the surface of the globe is projected onto a at map some aspects of the map are inevitably distorted. Mapmakers can choose which specic properties to preserve. For navigation at sea the angles between directions are critical. Mercator wanted angles on the map to correspond to angles on the sphere. This will only occur if the metric for the map is isotropic: gij is a multiple of the identity matrix, or equivalently ds2 has the factorised form ds2 = A(x, y )(dx2 + dy 2 ). (a) Starting from standard spherical polar coordinates show that the distance on a sphere of unit radius is given by the metric ds2 = d2 + cos2 d2 where is the longitude and =
2
(b) Now consider a transformation of coordinates to the 2D plane to draw maps. Let = x and let be some unknown function of y . Find the relationship between and y which makes the metric for the map isotropic and identify the common coecient A. It is convenient to make y = 0 the equator. (c) Rearrange the result from above to show that y and are related by the following interesting relations tan = sinh y sin = tanh y cos = sechy When these relationships hold y is said to be the Gudermannian of . You should now be able to write the coecient A as a function of y and thus have the metric in terms of the new variables. (d) Write down the Lagrangian that is equivalent to the metric you have found. Using rst integrals determine the equation for the shape of the geodesics. Show that sinh y = sin(x + ) where and are constants is the general solution (by substitution). Solution (a) Start from ds2 = d 2 + sin2 d2 . Since =
2
is the latitude.
then d = d and cos = sin thus ds2 = d2 + cos2 d2 .
(b) If we change variables the metric becomes ds2 = ( d 2 2 ) dy + cos2 dx2 . dy
106
2 2 which is isotropic if the two coecients are equal A = ( d dy ) = cos thus
d = cos dy We choose the positive sign so that the map will have north in the positive y direction (unless we want to make one of those upside-down Australia at the top-of-the-world maps. This rst order ODE can be solved by separation to give y= sec d = ln(sec + tan ) + C
We choose the constant C to be zero, so that the equator = 0 corresponds to the horizontal axis y = 0. We also have A(x, y ) = cos2 but we need to write this is terms of x and y which is the next part of the question. (c) Re-arrange to give exp(y ) = sec + tan and 1 sec tan = = sec tan sec + tan sec2 tan2 By adding and subtracting one can immediately get exp(y ) = tan = sinh y sec = cosh y The given relationships follow from these. We also thus have A(x, y ) = sech2 y or ds2 = sech2 (y )(dx2 + dy 2 ). (d) The equivalent Lagrangian is L= and the equivalent Hamiltonian is H= 1 2 cosh2 (y )(p2 x + py ). 2 1 sech2 (y )(x 2 + y 2 ). 2
Working with the Lagrangian we can identify two rst integrals (one for t and one for x) 1 2 + y 2) E = sech2 (y )(x 2 and P = sech2 (y )x Since we are interested in the shape of the geodesic we will also use for the rst derivative dy y = . dx x Combining these three results gives us the equation dy 2E = cosh2 (y )[1 + ( )2 ] 2 P dx 107
This equation can be solved by separation... however since I have told you the solution you can start with that and dierentiate it implicitly to nd cosh y Substituting this into the DE gives 2E = cosh2 (y ) + 2 cos2 (x + ) = 1 + sinh2 (y ) + 2 cos2 (x + ) P2 and then substituting in the expression for sinh(y ) gives 2E = 1 + 2 sin2 (x + ) + 2 cos2 (x + ) = 1 + 2 P2 Thus the equation does satisfy the DE. One of the two arbitrary constants is related to E and P as given above. The other arbitrary constant arises because you can choose the zero for longitude anyway you like: for example, passing through Greenwich in England. By the way, converting the curve back to longitude and latitude yields tan = sin( + ) or in spherical-polars cot = sin( + ) the SAME equation for a great circle that was obtained in an earlier tute. 2. An Area-preserving map A small element of area on the surface of a unit sphere is given by dAsphere = sin dd, whereas on a at map an element of area is dAf lat = dxdy . (a) Write the surface area element dAsphere in terms of the latitude . (b) Find a mapping x = and y = g() from the sphere to a plane that preserves area, dAsphere = dAf lat . (c) Starting with the distance between points on the sphere, show that the distance between points on the projected map is given by ds2 = (1 y 2 )dx2 + 1 dy 2 1 y2 dy = cos(x + ) dx
(d) Find the geodesics in terms of an integral. The integral is elliptic so do not try to do it. Solution (a) In terms of the latitude the surface area element is trivially cos dd. We do not need to worry about the minus sign. (b) If x = and y = g() then dxdy = g ()dd. Thus if area is preserved g () = cos . Thus g() = sin . (c) Thus dx = d and dy = cos d = 1 y 2 d. Thus since ds2 = d2 + cos2 d2 this gives 1 dy 2 1 y2
ds2 = (1 y 2 )dx2 +
108
(d) The equivalent Lagrangian is 1 1 2 + y 2] L = [(1 y 2 )x 2 1 y2 There are two rst integrals associated with t and x P = (1 y 2 )x and E= and we also use 1 1 [(1 y 2 )x 2 + y 2] 2 1 y2 y dy = . dx x 1 1 dy P 2 [1 + ( )2 ] 2(1 y 2 ) (1 y 2 )2 dx
which combine to give E= This can be rearranged to give (1 y 2 ) dy = dx P or separating variables to give x= We know that a great circle is tan = cot = sin( + ) So in terms of x and y we have . y 1 y2 = sin(x + ) (1 y 2 ) P dy 2(1 y 2 )E P 2 . 2(1 y 2 )E P 2
and one can show that this satises the DE given above.
109
You might also like
- SUMS Elementary Number Theory (Gareth A. Jones Josephine M. Jones) PDFDocument317 pagesSUMS Elementary Number Theory (Gareth A. Jones Josephine M. Jones) PDFtkov1100% (15)
- Chapter 3 TorsionDocument27 pagesChapter 3 TorsionAnonymous RGLhewESFNo ratings yet
- Sample Thesis WirelessDocument61 pagesSample Thesis WirelessRaymart MateoNo ratings yet
- Exercises: Double and Triple Integrals Solutions Math 13, Spring 2010Document8 pagesExercises: Double and Triple Integrals Solutions Math 13, Spring 2010Colls MuntadaNo ratings yet
- Notes On Vector CalculusDocument10 pagesNotes On Vector CalculusYukiNo ratings yet
- Special FunDocument10 pagesSpecial FunJHNo ratings yet
- D D 0 D D 0 D 0 0 2 0 D D 0 D 0 D D 0 D 0 0Document25 pagesD D 0 D D 0 D 0 0 2 0 D D 0 D 0 D D 0 D 0 0Anish Kumar DasNo ratings yet
- Vector Calculus Solutions RevisedDocument14 pagesVector Calculus Solutions RevisedCk ThewNo ratings yet
- Non Euclidean GeometryDocument9 pagesNon Euclidean GeometryBodhayan PrasadNo ratings yet
- Physics 2. Electromagnetism: 1 FieldsDocument9 pagesPhysics 2. Electromagnetism: 1 FieldsOsama HassanNo ratings yet
- Physics 139A Homework 1: 1 Problem 1.1Document10 pagesPhysics 139A Homework 1: 1 Problem 1.1a2618765No ratings yet
- CHP 7 ProblemsDocument5 pagesCHP 7 ProblemsaishaNo ratings yet
- MIT Multivariable Calculus Exam A SolutionsDocument16 pagesMIT Multivariable Calculus Exam A Solutions15klaNo ratings yet
- Hanging ChainDocument5 pagesHanging ChainŞener KılıçNo ratings yet
- HWSolution 2Document3 pagesHWSolution 2Touseef ahmadNo ratings yet
- − z and let ψ = xDocument7 pages− z and let ψ = xalpha2122No ratings yet
- Solutions5 PDFDocument8 pagesSolutions5 PDFShweta SridharNo ratings yet
- Homework 3 So LsDocument13 pagesHomework 3 So LsBrad StokesNo ratings yet
- Vector Calc Final Solutions - CaltechDocument7 pagesVector Calc Final Solutions - CaltechDezire GetNo ratings yet
- Mathematics, Computer Science and Joint Schools Wednesday 5 November 2014Document9 pagesMathematics, Computer Science and Joint Schools Wednesday 5 November 2014kheyNo ratings yet
- m2k DFQ SecordDocument11 pagesm2k DFQ SecordHaR's RicdNo ratings yet
- General Theory of Relativity For Undergraduates - Chapter 1Document29 pagesGeneral Theory of Relativity For Undergraduates - Chapter 1Alexandre Masson VicenteNo ratings yet
- Homework 4 SolDocument6 pagesHomework 4 SoljanroxaNo ratings yet
- Lecture 39: The Divergence Theorem: Dy Ds DX Ds DX Ds Dy DsDocument2 pagesLecture 39: The Divergence Theorem: Dy Ds DX Ds DX Ds Dy DsnairavnasaNo ratings yet
- Problem Solving 1: Line Integrals and Surface Integrals A. Line IntegralsDocument11 pagesProblem Solving 1: Line Integrals and Surface Integrals A. Line IntegralsAlexis SalvadorNo ratings yet
- Greens TheoremDocument9 pagesGreens TheoremAnonymous KIUgOYNo ratings yet
- BaristocranaDocument3 pagesBaristocranajonnathan_andreNo ratings yet
- Adm Formulation of GRDocument6 pagesAdm Formulation of GRMobashar AhmadNo ratings yet
- Example of The Use of Stokes TheoremDocument3 pagesExample of The Use of Stokes TheoremSam FraserNo ratings yet
- Normal PDFDocument5 pagesNormal PDFjohngreen13No ratings yet
- Outline of Solutions To Homework 1Document3 pagesOutline of Solutions To Homework 1Michel AndradeNo ratings yet
- Gold ProblemsDocument13 pagesGold ProblemsoitlaliNo ratings yet
- 1 Method of Images: Plane BoundaryDocument25 pages1 Method of Images: Plane BoundaryRoshan ShresthaNo ratings yet
- Common Fixed Points For Weakly Compatible Maps: Renu Chugh and Sanjay KumarDocument7 pagesCommon Fixed Points For Weakly Compatible Maps: Renu Chugh and Sanjay Kumarjhudddar99No ratings yet
- SSM Ch18Document106 pagesSSM Ch18jacobsrescue11100% (1)
- Sec11 PDFDocument4 pagesSec11 PDFRaouf BouchoukNo ratings yet
- Calculus AB & BC Solutions 2014Document10 pagesCalculus AB & BC Solutions 2014gboover123100% (1)
- 2.11 Example Metric For 3D Flat SpaceDocument4 pages2.11 Example Metric For 3D Flat SpaceAmalendu PramanickNo ratings yet
- Engineering Electrodynamics MidtermDocument36 pagesEngineering Electrodynamics MidtermSrinivas PrasadNo ratings yet
- The Hypergeometric Differential Equation With Cubic Curves As Schwarz ImagesDocument20 pagesThe Hypergeometric Differential Equation With Cubic Curves As Schwarz Images3873263No ratings yet
- Lec Week10Document4 pagesLec Week10Haripriya RadhakrishnanNo ratings yet
- 2013 Homework 012solDocument2 pages2013 Homework 012soleouahiauNo ratings yet
- 2.1 Double IntegralsDocument8 pages2.1 Double Integralsmukesh3021No ratings yet
- Jan98 MA1002 CalculusDocument6 pagesJan98 MA1002 CalculusZama MakhathiniNo ratings yet
- Ellipsoid PotentialDocument18 pagesEllipsoid PotentialEduardoHenriquezNo ratings yet
- MA3264Tutorial1 Solutions by LinDocument10 pagesMA3264Tutorial1 Solutions by LinTim CookNo ratings yet
- Chap 1 and 2Document7 pagesChap 1 and 2ismaeil1365No ratings yet
- HW 1 SolDocument3 pagesHW 1 SoljigyansuNo ratings yet
- Solutions To Homework 5Document6 pagesSolutions To Homework 5David G. MirandaNo ratings yet
- Outline CD 2Document9 pagesOutline CD 2Imdadul HaqueNo ratings yet
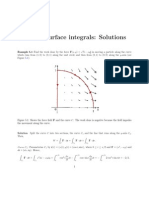
- Line and Surface Integrals: Solutions: Example 5.1Document7 pagesLine and Surface Integrals: Solutions: Example 5.1Paul Reyna RojasNo ratings yet
- Defslt Lec # 03 13-01-21Document7 pagesDefslt Lec # 03 13-01-21AkashNo ratings yet
- 9 Riemannian MetricsDocument14 pages9 Riemannian MetricsleorefasolNo ratings yet
- Efficient Arithmetic On Elliptic Curves Using A Mixed Edwards-Montgomery RpresentationDocument4 pagesEfficient Arithmetic On Elliptic Curves Using A Mixed Edwards-Montgomery RpresentationCRISTOPHER MANUEL SALINAS MORALESNo ratings yet
- 9 Multivariable FunctionsDocument5 pages9 Multivariable FunctionsslowjamsNo ratings yet
- Example of The Use of Stokes' TheoremDocument3 pagesExample of The Use of Stokes' Theoremmohamed elfekyNo ratings yet
- Sample Test 2 SolDocument6 pagesSample Test 2 Solching chauNo ratings yet
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsFrom EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsNo ratings yet
- A-level Maths Revision: Cheeky Revision ShortcutsFrom EverandA-level Maths Revision: Cheeky Revision ShortcutsRating: 3.5 out of 5 stars3.5/5 (8)
- Trigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsFrom EverandTrigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- A Quantum Mechanic's ManualDocument12 pagesA Quantum Mechanic's ManualShweta SridharNo ratings yet
- Lecture 9 ABC, CVP PDFDocument58 pagesLecture 9 ABC, CVP PDFShweta SridharNo ratings yet
- Calculus: Fundamental TheoremDocument4 pagesCalculus: Fundamental TheoremShweta SridharNo ratings yet
- Classical Mechanics Homework 10Document2 pagesClassical Mechanics Homework 10Shweta SridharNo ratings yet
- Classical Mechanics Homework 11Document4 pagesClassical Mechanics Homework 11Shweta SridharNo ratings yet
- Classical Mechanics Homework 12Document2 pagesClassical Mechanics Homework 12Shweta SridharNo ratings yet
- Vector Calculus: Notes For Math1c, Spring Term 2011Document15 pagesVector Calculus: Notes For Math1c, Spring Term 2011Shweta SridharNo ratings yet
- Physics 127a: Class Notes: Lecture 17: Ideal Fermi GasDocument7 pagesPhysics 127a: Class Notes: Lecture 17: Ideal Fermi GasShweta SridharNo ratings yet
- Derivation of Clausius Clapeyron Equation PDFDocument1 pageDerivation of Clausius Clapeyron Equation PDFShweta SridharNo ratings yet
- ThermistorsDocument3 pagesThermistorsAbraham96No ratings yet
- Comprehensive Reading-PS - "Heaviest Elements Did Not Form From Supernova"Document2 pagesComprehensive Reading-PS - "Heaviest Elements Did Not Form From Supernova"Chona CamposanoNo ratings yet
- Magnetic Resonant AmplifierDocument31 pagesMagnetic Resonant Amplifierlittledigger100% (7)
- Linear AdvectionDocument21 pagesLinear AdvectionKenneth DavisNo ratings yet
- Robot ManipulatorDocument47 pagesRobot ManipulatorumamaheswariNo ratings yet
- Problem SetDocument2 pagesProblem SetPhan MiNo ratings yet
- Chapter 7 Analysis of Stress and StrainDocument20 pagesChapter 7 Analysis of Stress and StrainLong Nguyễn HoàngNo ratings yet
- Harmonic Response Analysis: I. Two Mass Spring SystemDocument5 pagesHarmonic Response Analysis: I. Two Mass Spring SystemDinesh_Tadkapa_62No ratings yet
- Chemistry Review SheetDocument9 pagesChemistry Review SheetEric ThatAsian Yao100% (1)
- As Physics Jan 9Document20 pagesAs Physics Jan 9Tayyaba Mumtaz KhanNo ratings yet
- Critical Coupling, Oscillation, Reflection, and Transmission in Optical Waveguide-Ring Resonator SystemsDocument8 pagesCritical Coupling, Oscillation, Reflection, and Transmission in Optical Waveguide-Ring Resonator SystemsArnab PattanayakNo ratings yet
- CapacitorsDocument30 pagesCapacitorsKovid BalliNo ratings yet
- Us 512340Document3 pagesUs 512340Mihai RobertNo ratings yet
- Syllabus - KTU - S1 and S2Document65 pagesSyllabus - KTU - S1 and S2AnilaPraveenNo ratings yet
- General Chemistry 2: Quarter 4 - Module 1: Second Law of ThermodynamicsDocument27 pagesGeneral Chemistry 2: Quarter 4 - Module 1: Second Law of ThermodynamicsAriane Valdez100% (1)
- Unit1 5 Problems On MechanismsDocument12 pagesUnit1 5 Problems On MechanismsKarthikayan Balaji100% (2)
- Homework # 3 - WWWR #18.18, 18.27. - ID # 5.5, 5.8.: (Self Practice)Document43 pagesHomework # 3 - WWWR #18.18, 18.27. - ID # 5.5, 5.8.: (Self Practice)Diana JenkinsNo ratings yet
- Nano Assesment-1 Question PaperDocument3 pagesNano Assesment-1 Question Paperdineshkumarbaskaran100% (3)
- Eddycurrentbrakes 140401105112 Phpapp01Document23 pagesEddycurrentbrakes 140401105112 Phpapp01umangNo ratings yet
- Slope Deflection Method - Draft PDFDocument35 pagesSlope Deflection Method - Draft PDFRhina Dhel CarpioNo ratings yet
- Review Enhancement of Heat Transfer Through Modification in FinsDocument9 pagesReview Enhancement of Heat Transfer Through Modification in FinsIJRASETPublicationsNo ratings yet
- Offshore Pipe Line Design State of The ArtDocument33 pagesOffshore Pipe Line Design State of The ArtMvrnaidu MithraNo ratings yet
- Introduction To PhysicsDocument29 pagesIntroduction To PhysicsDesikan Subramaniam33% (3)
- MasteringPhysics Answers SOLUTIONSDocument139 pagesMasteringPhysics Answers SOLUTIONSgdfeiu dionwdn0% (1)
- Design of Low Pass Filter Using Micro Strip LinesDocument14 pagesDesign of Low Pass Filter Using Micro Strip LinesSakshiKoulNo ratings yet
- The Purpose / Social Function of Explanation TextDocument5 pagesThe Purpose / Social Function of Explanation TextBetabara Sinamo100% (1)
- 1.C-10-T1 - 01 ATOMIC STRUCTURE Pace FBDocument33 pages1.C-10-T1 - 01 ATOMIC STRUCTURE Pace FBriddhiNo ratings yet
- Hxe320 User Mannual V2Document57 pagesHxe320 User Mannual V2IBMANNo ratings yet