The Discrete Fourier Transform (DFT)

Introduction
Here we will start with the Fourier series of a band-limited, periodic function and see what happens when it
is sampled using Ideal sampling. The result will be the Discrete Fourier Transform (DFT). We can then
understand the characteristics of periodic, discrete-time signals in the freuenc! domain.
The Periodic Signal
"ssume #(t) is a band-limited, periodic function with ma#imum freuenc! W and period T. Its comple#
e#ponential series can then be written as$
( )

+

%
&
%
%
'
N
N
i
t
T
i
j
i
X t x

Where ()% * WT is sufficient to co+er all the non-,ero coefficients (those with low enough energ! to be
appro#imated awa!) and$
( )

T t
T
i
j
i
dt t x
T
X
-
%
'
&

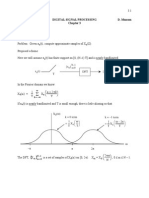
The Fourier Transform, .(/), of #(t) is then a finite sum of -functions and can be s0etched as a function
of freuenc!.
X(f)
0
0.2
0.4
0.6
0.8
1
1.2
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
Frequency index (i)
1. (. Denenberg 2op!right DT3 1une &4, %--5
DFT Tutorial 6age % of 7
Sampling x(t)
If we now sample (we shall assume Ideal sampling to simplif! the deri+ation) #(t) at the (!uist rate of %W,
the spectrum becomes periodic as was determined in the discussion on sampling. The spectrum also gets a
gain factor (not discussed earlier) which is introduced in the sampling process.
Assume that we sample f(t) ideally over the time interval (0, a) with n samples.
( )

,
_

,
_

N
a
k t
N
a
k f T t f
N k
k
' ,
&
-
nte!ratin! (usin! the siftin! property of "fun#tions)
( )

,
_

&
-
-
,
N k
k
a
N
a
k f dt T t f
$ut
( )

,
_

,
_

&
-
&
-
-
'
N k
k
N k
k
a
N
a
k f
N
a
N
a
N
a
k f dt t f
%o the sampled fun#tion is N&a time stron!er than the ori!inal. 'e #an adjust for this (y
s#alin! the impulse train (y T&) in our development.
"nd
( )

,
_

,
_

N
a
k t
N
a
k x
)
T
T t x
N k
k
' ,
&
-
Where 8 is the largest integer that corresponds to a freuenc! that is less than %TW at the selected sampling
rate.
The Fourier series for the discrete-time signal is then

,
_

%
&
%
%
'
N
N
i
ik
)
j
i k
X x
)
kT
t x

9r, if we sample at e#actl! the (!uist rate, 8:( and

%
&
%
%
'
N
N
i
ik
N
j
i k
X x

9r 3ince the .
i
are periodic with period (

&
-
%
'
N
i
ik
N
j
i k
X x

Which is one half of the two DFT euations

1. (. Denenberg 2op!right DT3 1une &4, %--5
DFT Tutorial 6age 4 of 7
The second half of the DFT is obtained b! starting with
( )

T t
T
i
j
i
dt T t x
T
X
-
%
' ,
&

We can now substitute the sampling sum of -functions for #(t,T)

1
]
1

,
_

T t
T
i
j
N k
k
k i
dt
N
T
k t x
N
T
T
X
-
%
&
-
' '
&


Interchanging the order of integration and summation and again using the sifting propert! of -functions
!ields the second half of the DFT pair
ik
N
j
N k
k
k i
x
N
X

%
&
-
'
&

9ften these two euations are simplified b! assuming that

N
j
N
'

;esulting in the DFT transform pair

Direct DFT
ik
N
k
k i
' x
N
X

'
&
&
-
In+erse DFT

&
-
'
N
i
ik
i k
' X x
It should be noted that the &)( factor is sometimes placed in the In+erse DFT euation. This can be a source
of confusion.
DFT: The Matrix Formulation
The euations abo+e can be restated as a pair of matri# euations. <et
( ) ( )
( ) ( )
( ) ( )
1
1
1
1
1
1
]
1

%
%
& & -
% % -
& % & -
- - - -
...
... ...
...
...
n n
n n
n n
' ' '
' ' '
' ' ' '
' ' ' '
'

then, it=s in+erse is

( ) ( )
( ) ( )
( ) ( )
1
1
1
1
1
1
]
1

%
%
& & -
% % -
& % & -
- - - -
&
...
... ...
...
...
n n
n n
n n
' ' '
' ' '
' ' ' '
' ' ' '
'

1. (. Denenberg 2op!right DT3 1une &4, %--5

DFT Tutorial 6age 7 of 7
(ow define
( )
( )
1
1
1
1
1
1
]
1

&
%
&
-
...
n
n
X
X
X
X
X

and
( )
( )
1
1
1
1
1
1
]
1

&
%
&
-
...
n
n
x
x
x
x
x

The DFT transform pair is then gi+en b! the matri# euations

x '
N
X


' '
&

and X ' x

'
&

1. (. Denenberg 2op!right DT3 1une &4, %--5