Professional Documents
Culture Documents
Math 634 Lecture #33 2.4.4: Stability of Periodic Orbits, Part II
Math 634 Lecture #33 2.4.4: Stability of Periodic Orbits, Part II
Uploaded by
An JiangOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Math 634 Lecture #33 2.4.4: Stability of Periodic Orbits, Part II
Math 634 Lecture #33 2.4.4: Stability of Periodic Orbits, Part II
Uploaded by
An JiangCopyright:
Available Formats
Math 634 Lecture #33
2.4.4: Stability of Periodic Orbits, Part II
For our next step, we will connect the asymptotic stability of the Poincare map P : S
at a xed point p with that of the asymptotic stability of the periodic of the ow
u(t, ) for u = f(u).
Dene the distance between two sets A, B R
n
by
dist(A, B) = inf{|a b| : a A, b B}.
Proposition 2.129. For , if lim
n
P() = p, then
lim
n
dist(u(t, ), ) = 0.
Proof. Let > 0 and let
0
be an open subset of such that p and
0
is a compact
subset of .
Since the return time map T : R is continuous, its restriction to
0
is uniformly
continuous.
This implies that
T
= sup{T() :
0
} < .
Let V be an open subset of R
n
with V compact such that V and V is a subset of the
domain of f.
By Lemma 2.128, there is an open set W V such that W and for each W, the
solution u(t, ) remains in V on the interval [0, T
].
Let m = dist(, V ), and let L be the Lipschitz constant for f on V .
Choose > 0 such that
= { : | p| < }
is contained in W
0
and for all
there holds
| p|e
LT
< min{m, }.
By Lemma 2.128, when
then for all 0 s T
there holds
|u(s, ) u(s, p)| < | p|e
LT
< .
By hypothesis, there is N N such that for all n N we have P
n
()
.
By the group property of the ow u(t, ) we have that
P
n
() = u
_
n1
j=0
T(P
j
()),
_
.
For t
n1
j=0
T(P
j
()), there is some n N and some s with 0 s T
such that
t =
n1
j=0
T(P
j
()) +s.
For this t we have
dist(u(t, ), ) = min
q
|u(t, ) q|
|u(t, ) u(s, p)|
=
u
_
s +
n1
j=0
T(P
j
()),
_
u(s, p)
u
_
s, u
_
n1
j=0
T(P
j
()),
__
u(s, p)
= |u(s, P
n
()) u(s, p)|
which implies that dist(u(t, ), ) < .
Now we are nally ready for the stability result.
Theorem 2.124. Suppose that is a periodic orbit of u = f(u) and P : S is a
Poincare map with p . If the eigenvalues of DP(p) all lie inside the unit circle, then
is asymptotically stable.
Proof. To get the (orbital) asymptotic stability of , we must nd, for each open set V
containing an open set U containing with U V such that every solution that starts in
U stays in V and is asymptotic to .
WLOG we assume that V is compact and contained in the domain of f.
Let = T(p), the period of the periodic orbit .
By Lemma 2.128, there is an open subset W of V such that every solution starting in W
exists and stays in V on the time interval 0 t 2.
Also, WLOG, we assume that the Poincare section is part of the hyperplane S at p
perpendicular to f(p), and coordinates on S are chosen so that p lies at the origin.
By hypothesis, the map DP(0) : S S has its spectrum inside the unit circle.
By Corollary 2.127, there exists an adapted norm
a
on R
n
and a number 0 < < 1 such
that induced operator norm DP(0) < .
Using the continuity of DP(), the return time map T : R, and the adapted
norm, there is an open ball
0
centered at the origin such that
0
W, the return
time map T restricted to
0
is bounded above by 2 and below by /2, and DP() <
for all
0
.
By the Mean Value Theorem we have
P()
a
= P() P(0)
a
sup
0
DP() 0
a
<
a
whenever
0
, so that P is a contraction mapping, meaning that lim
j
P
j
() = 0.
In particular, if
0
then P()
0
.
We will show as a consequence, that any solution staring at
0
is dened for all t 0.
The solution t u(t, ) is dened for 0 t T() because T() < 2.
Since u(T(), ) = P()
0
, the domain of solution t u(t, ) extends to T()+T(P()).
Repeating this argument we get the domain of t u(t, ) is t 0 because T() /2 for
all
0
.
We dene the desired subset U by
U = {u(t, ) :
0
, t > 0}.
Every solution that starts in U stays in U by denition.
Because 0
0
corresponds to p , we have U.
To show that U is open, we consider
0
= u(t
0
,
0
) for t
0
> 0 and
0
0
.
For R
n
close enough to
0
, we have by continuity of solutions with respect to initial
conditions that u(t, ) stays close to u(t,
0
) for all t in (t
0
1, 0).
By the Rectication Lemma (with Section) applied at 0, there is t
in (t
0
1, 0) such that
u(t
, ) =
0
where t
is close to t
0
.
Then = u(t
, u(t
, )) = u(t
) where t
> 0 and
0
.
This implies that every point in an small enough open ball centered at
0
is of the form
u(t, ) for t > 0 and
0
.
Thus U is open.
To show that U V , we again let = u(t, ) U with
0
.
Then there is some integer n 0 and some real number s such that
t =
n1
j=0
T(P
j
()) +s
where 0 s < T(P
n
()) < 2.
Since P
n
()
0
W and = u(s, P
n
()), it follows that V .
(Recall that starting in W means staying in V on the time interval [0, 2].)
Finally, for this same = u(s, P
n
()) U where P
n
()
0
satises lim
j
P
j
(P
n
()) = 0,
it follows from Proposition 2.129 that
lim
t
dist(u(t, P
n
()), ) = 0.
For all t 0 we have
dist(u(t, ), ) = dist
_
u(t, u(s, P
n
())),
_
= dist(u(t +s, P
n
()), ).
Therefore, we arrive at the asymptotic stability lim
t
dist(u(t, )), ) = 0.
Homework. None.
You might also like
- The Fabric Formwork Book PDFDocument318 pagesThe Fabric Formwork Book PDFtoth_daniel75% (4)
- Homework5 Solution PDFDocument4 pagesHomework5 Solution PDFKensleyTsangNo ratings yet
- Solutions of Exercises In: Dongkwan KimDocument31 pagesSolutions of Exercises In: Dongkwan Kimalgohrythm100% (1)
- Lecture 10Document3 pagesLecture 10ThetaOmegaNo ratings yet
- Duhamel's PrincipleDocument6 pagesDuhamel's PrinciplezelihahaNo ratings yet
- J If P (I, J) 0, Where P Is The Transition Probability. Note 2 1 0Document2 pagesJ If P (I, J) 0, Where P Is The Transition Probability. Note 2 1 0Jung Yoon SongNo ratings yet
- Equivalence Between Entropy and Renormalized Solutions For Parabolic Equations With Smooth Measure Data - Jerome DRONIOUDocument25 pagesEquivalence Between Entropy and Renormalized Solutions For Parabolic Equations With Smooth Measure Data - Jerome DRONIOUJefferson Johannes Roth FilhoNo ratings yet
- Problem Set 4 - SolutionDocument2 pagesProblem Set 4 - SolutiondamnedchildNo ratings yet
- Results About Heat EquationsDocument7 pagesResults About Heat EquationsAdi SubbuNo ratings yet
- TopicsDocument41 pagesTopicsJoshuaHaimMamouNo ratings yet
- Math 104 - Homework 10 Solutions: Lectures 2 and 4, Fall 2011Document4 pagesMath 104 - Homework 10 Solutions: Lectures 2 and 4, Fall 2011dsmile1No ratings yet
- CringanuDocument10 pagesCringanuJessica GreeneNo ratings yet
- Arithmetic Properties of The Ramanujan FunctionDocument8 pagesArithmetic Properties of The Ramanujan Functionapi-26401608No ratings yet
- Complemento Uchile (Semigrupos)Document18 pagesComplemento Uchile (Semigrupos)robertoNo ratings yet
- u u, x ∈ Ω, t ∈ (0, ∞), u = 0, x ∈ ∂Ω, t ∈ (0, ∞), u (x, 0) = u x ∈ Ω,Document9 pagesu u, x ∈ Ω, t ∈ (0, ∞), u = 0, x ∈ ∂Ω, t ∈ (0, ∞), u (x, 0) = u x ∈ Ω,szsannnNo ratings yet
- Heat Flow, or Diffusion, PdeDocument4 pagesHeat Flow, or Diffusion, PdeIsmael ArceNo ratings yet
- 501 4Document8 pages501 4Antonio Hernandez OrozcoNo ratings yet
- Math 322 Homework 10: December 5, 2011Document4 pagesMath 322 Homework 10: December 5, 2011Liyang ZhangNo ratings yet
- 2021 Geometry Study Guide 4Document24 pages2021 Geometry Study Guide 4JacmNo ratings yet
- Assignment FINALDocument67 pagesAssignment FINALlaila khanNo ratings yet
- Communications On Pure and Applied Analysis Volume 6, Number 1, March 2007Document20 pagesCommunications On Pure and Applied Analysis Volume 6, Number 1, March 2007Mouhcine AsNo ratings yet
- Cauchy Covaleviski PDFDocument12 pagesCauchy Covaleviski PDFDede SantosNo ratings yet
- 3.point Set TopologyDocument98 pages3.point Set TopologyVijay ChhipaNo ratings yet
- Dedicated To Professor Nirenberg On His BirthdayDocument11 pagesDedicated To Professor Nirenberg On His Birthdaytemneanu1962No ratings yet
- c15 Laplace Trans PdesDocument10 pagesc15 Laplace Trans PdesChristina HillNo ratings yet
- Assn1 M146CDocument8 pagesAssn1 M146CRaymondSanchezNo ratings yet
- CyclotomicperiodsDocument7 pagesCyclotomicperiodsjoseluisapNo ratings yet
- Example SheetDocument22 pagesExample SheetBikash Tamu100% (1)
- Headsoln Master MethodDocument6 pagesHeadsoln Master MethodSumit DeyNo ratings yet
- Protter SolutionsDocument25 pagesProtter Solutionsbobobobob3264No ratings yet
- Thermo NotesDocument12 pagesThermo NotesSamriddha Das GuptaNo ratings yet
- Probabilistic Modelling and ReasoningDocument13 pagesProbabilistic Modelling and ReasoningAlex McMurrayNo ratings yet
- Birkhoff G.D. - Prueba Del Teorema Ergódico (1931)Document5 pagesBirkhoff G.D. - Prueba Del Teorema Ergódico (1931)SamirL.SánchezNo ratings yet
- C Irc Atm Ciclu EnergeticDocument19 pagesC Irc Atm Ciclu EnergeticRada IoanNo ratings yet
- t T T T 1 α α T 1 T 2 α T 2 t=0 3 1 2 3 3 1 1 2 3 3 1 2 3 α 3Document17 pagest T T T 1 α α T 1 T 2 α T 2 t=0 3 1 2 3 3 1 1 2 3 3 1 2 3 α 3phanvandu09No ratings yet
- Solution For Chapter 23: T T' P T' T T' T PDocument8 pagesSolution For Chapter 23: T T' P T' T T' T PSveti JeronimNo ratings yet
- Stochastic Calculus For Finance II - Some Solutions To Chapter IIIDocument9 pagesStochastic Calculus For Finance II - Some Solutions To Chapter IIIMaurizio BarbatoNo ratings yet
- Equadiff Vienne 2007Document6 pagesEquadiff Vienne 2007hhedfiNo ratings yet
- Take-Home Test 1 Solutions: 6.243J (Fall 2003) : Dynamics of Nonlinear Systems by A. MegretskiDocument5 pagesTake-Home Test 1 Solutions: 6.243J (Fall 2003) : Dynamics of Nonlinear Systems by A. Megretskihulier2No ratings yet
- Lec 20Document8 pagesLec 20Angelo OppioNo ratings yet
- Lipschitz Continuity and SemiconcDocument14 pagesLipschitz Continuity and Semiconctakamiya980921No ratings yet
- GR On Wall InequalityDocument4 pagesGR On Wall InequalityOgugua OnyejekweNo ratings yet
- Adaptive Lecture04 2005Document28 pagesAdaptive Lecture04 2005Cuter HsuNo ratings yet
- HW 04 Wells 598Document5 pagesHW 04 Wells 598funkmetalbassNo ratings yet
- On The Value Set of The Ramanujan FunctionDocument6 pagesOn The Value Set of The Ramanujan Functionapi-26401608No ratings yet
- Chapter 14Document22 pagesChapter 14서승찬No ratings yet
- Solutions For Chapter III. Updated January 20, 2007.: R S N MDocument17 pagesSolutions For Chapter III. Updated January 20, 2007.: R S N Myacp16761No ratings yet
- Chapter 3: Baire Category and Open Mapping Theo-RemsDocument8 pagesChapter 3: Baire Category and Open Mapping Theo-RemsKhmer ChamNo ratings yet
- Stochastic Calculus For Discontinuous ProcessesDocument20 pagesStochastic Calculus For Discontinuous Processesjulianli0220No ratings yet
- The Method of Characteristics Applied To Quasi-Linear PDEsDocument11 pagesThe Method of Characteristics Applied To Quasi-Linear PDEsAmit RaiNo ratings yet
- L07 NotesDocument4 pagesL07 Notesabu453014No ratings yet
- Chap 5Document5 pagesChap 5Ariana Ribeiro LameirinhasNo ratings yet
- Dupont - Fiber Bundles in Gauge TheoryDocument109 pagesDupont - Fiber Bundles in Gauge TheoryWilfred HulsbergenNo ratings yet
- Harmonic Maps and Minimal Immersions with Symmetries (AM-130), Volume 130: Methods of Ordinary Differential Equations Applied to Elliptic Variational Problems. (AM-130)From EverandHarmonic Maps and Minimal Immersions with Symmetries (AM-130), Volume 130: Methods of Ordinary Differential Equations Applied to Elliptic Variational Problems. (AM-130)No ratings yet
- Discrete Series of GLn Over a Finite Field. (AM-81), Volume 81From EverandDiscrete Series of GLn Over a Finite Field. (AM-81), Volume 81No ratings yet
- Commensurabilities among Lattices in PU (1,n). (AM-132), Volume 132From EverandCommensurabilities among Lattices in PU (1,n). (AM-132), Volume 132No ratings yet
- The Spectral Theory of Toeplitz Operators. (AM-99), Volume 99From EverandThe Spectral Theory of Toeplitz Operators. (AM-99), Volume 99No ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- John Nash Thesis LengthDocument4 pagesJohn Nash Thesis Lengthmaureennonweilertulsa100% (2)
- Lecture 00Document10 pagesLecture 00Samy YNo ratings yet
- Narayana Medical Academy, India: A K KXDocument4 pagesNarayana Medical Academy, India: A K KXIhtisham Ul HaqNo ratings yet
- FEA Assignment OTHERDocument13 pagesFEA Assignment OTHERZeashaan AkhmedNo ratings yet
- 2016 SIOMM Brochure - CompressedDocument27 pages2016 SIOMM Brochure - CompressedDaisy HeNo ratings yet
- Large Web Openings For Service Integration in Composite FloorsDocument121 pagesLarge Web Openings For Service Integration in Composite FloorsStephen HicksNo ratings yet
- BHNK Drill Pipe CatalogDocument12 pagesBHNK Drill Pipe CatalogivertianNo ratings yet
- PHY411 Lecture Notes Part 2: Alice Quillen October 2, 2018Document40 pagesPHY411 Lecture Notes Part 2: Alice Quillen October 2, 2018Lombardo BackupNo ratings yet
- A2 Answers To Energetics QuestionsDocument10 pagesA2 Answers To Energetics QuestionsmasudrhussainNo ratings yet
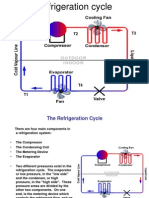
- RAC CycleDocument10 pagesRAC CyclekavooriNo ratings yet
- Biomed IncDocument48 pagesBiomed IncriddhiNo ratings yet
- Bacterial Detection Live Dead PDFDocument6 pagesBacterial Detection Live Dead PDFMuhamad ZakyNo ratings yet
- Tia Eia 568 B.3Document34 pagesTia Eia 568 B.3Ricardo Betancourt MaldonadoNo ratings yet
- Exam2 100b w21Document4 pagesExam2 100b w21AbigailNo ratings yet
- Lab 15 Specific Heat of An Unknown MetalDocument12 pagesLab 15 Specific Heat of An Unknown Metaljohn linNo ratings yet
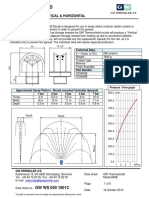
- WS 050 1001 C Thermoshield Model 883BDocument6 pagesWS 050 1001 C Thermoshield Model 883Bcandra trisilawatiNo ratings yet
- Science-2010-786-Cho - Energy's Tricky Tradeoffs PDFDocument2 pagesScience-2010-786-Cho - Energy's Tricky Tradeoffs PDFpablocolindresNo ratings yet
- Human Eye Complete - Watermarked PDFDocument13 pagesHuman Eye Complete - Watermarked PDFanandatulNo ratings yet
- MCQDiscrete IIISemDocument17 pagesMCQDiscrete IIISemtbuvaneswari2176No ratings yet
- Homogeneity and Stability of Reference 3Document6 pagesHomogeneity and Stability of Reference 3Raphael yagamiNo ratings yet
- All About Cholesky MatrixDocument6 pagesAll About Cholesky MatrixMarioImprontaNo ratings yet
- Lecture Planner - AIR JEEDocument2 pagesLecture Planner - AIR JEEkharevinayak32No ratings yet
- Carrier RESDocument18 pagesCarrier RESUNIQUENo ratings yet
- PED TRNG Feb01Document86 pagesPED TRNG Feb01Eric StewartNo ratings yet
- SPE 39895 Improved Selection of Candidates For StimulationDocument9 pagesSPE 39895 Improved Selection of Candidates For StimulationJesus Ponce GNo ratings yet
- 5.33 Lecture Notes: A Classical Description of Absorption: Why Is There Light Absorption?Document10 pages5.33 Lecture Notes: A Classical Description of Absorption: Why Is There Light Absorption?Dhimant UpadhyayNo ratings yet
- Rpla 2MDocument22 pagesRpla 2MnandhinicaratNo ratings yet
- Tolerances and BackfillingDocument4 pagesTolerances and BackfillingAjitesh YelisettyNo ratings yet