Professional Documents
Culture Documents
AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2
AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2
Uploaded by
jimmytanlimlongCopyright:
Available Formats
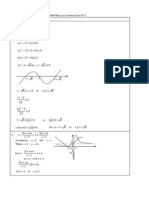
You might also like
- BMC Helix IT Service Management Deployment 22.1.06: Technical DocumentationDocument486 pagesBMC Helix IT Service Management Deployment 22.1.06: Technical DocumentationSupria GeraNo ratings yet
- Lesson Three Hair AppointmentDocument10 pagesLesson Three Hair AppointmentHassanNo ratings yet
- MJC JC2 H2 Maths 2012 Year End Exam Paper 2 Solutions PDFDocument10 pagesMJC JC2 H2 Maths 2012 Year End Exam Paper 2 Solutions PDFRyan LeeNo ratings yet
- 2016-Acjc-Promo-Scan (9758)Document22 pages2016-Acjc-Promo-Scan (9758)Simon AngNo ratings yet
- 2016 NJC H2 Maths PromoDocument18 pages2016 NJC H2 Maths Promomadhih123No ratings yet
- 2009 NJC SH2 H2 Mathematics Prelim Paper 2 SolutionsDocument21 pages2009 NJC SH2 H2 Mathematics Prelim Paper 2 SolutionsNicholas ChoyNo ratings yet
- CJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesCJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2007 Paper 2 Chemistry: Topic: Introduction To Organic ChemistryDocument11 pages2007 Paper 2 Chemistry: Topic: Introduction To Organic ChemistrysaffronNo ratings yet
- 2009 RI Prelims Chem H2 P3 AnsDocument7 pages2009 RI Prelims Chem H2 P3 AnsJasonNo ratings yet
- VJC h2 Math p2 SolutionsDocument4 pagesVJC h2 Math p2 Solutionsjimmytanlimlong100% (1)
- NJC h2 Math p2 Annex BDocument2 pagesNJC h2 Math p2 Annex BjimmytanlimlongNo ratings yet
- CJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesCJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- RI H2 Maths 2013 Prelim P1 SolutionsDocument13 pagesRI H2 Maths 2013 Prelim P1 Solutionsnej200695100% (1)
- 2014 H2 Maths Prelim Papers - HCI P2 Solution PDFDocument14 pages2014 H2 Maths Prelim Papers - HCI P2 Solution PDFcherylhzy100% (1)
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document10 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2015 JC2 H2 Maths Victoria Junior College PDFDocument33 pages2015 JC2 H2 Maths Victoria Junior College PDFVu Quang MinhNo ratings yet
- ACJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument6 pagesACJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2019 Y5 Promo Revision (Sem1 Topics)Document10 pages2019 Y5 Promo Revision (Sem1 Topics)Sarah RahmanNo ratings yet
- AJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document3 pagesAJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- Nyjc h2 Math p1 SolutionDocument10 pagesNyjc h2 Math p1 SolutionjimmytanlimlongNo ratings yet
- IJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document8 pagesIJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- 2012 ACJC Prelim H2 Math SolnDocument15 pages2012 ACJC Prelim H2 Math Solnckhowh_23284524667% (3)
- Sajc 2010 Prelim Math p1 SolnDocument10 pagesSajc 2010 Prelim Math p1 SolnAh XiuNo ratings yet
- 2007 IJC PrelimDocument23 pages2007 IJC PrelimWen LongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document10 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- IJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document8 pagesIJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- Teorema Limit, Satu Sisi, Apit, Trigonometri&Tak HinggaDocument117 pagesTeorema Limit, Satu Sisi, Apit, Trigonometri&Tak HinggaSari IndahNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document11 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- NJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument10 pagesNJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1Document18 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1jimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2Document15 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2jimmytanlimlongNo ratings yet
- JC 1 H2 Maths Promo Practice Paper 1Document6 pagesJC 1 H2 Maths Promo Practice Paper 1brianfletcher182No ratings yet
- TJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument12 pagesTJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- 2014 H2 Maths Prelim Papers - NJC P1 SolutionDocument13 pages2014 H2 Maths Prelim Papers - NJC P1 Solutioncherylhzy0% (4)
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document7 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document10 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongNo ratings yet
- CJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument5 pagesCJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument9 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- Ri h2 Math p2 SolutionsDocument11 pagesRi h2 Math p2 SolutionsjimmytanlimlongNo ratings yet
- ACJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 pagesACJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- RI JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRI JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1Document8 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1jimmytanlimlongNo ratings yet
- AJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 pagesAJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongNo ratings yet
- 2012 A Level H2 Chemistry Paper 2 Modified For New Syllabus PDFDocument10 pages2012 A Level H2 Chemistry Paper 2 Modified For New Syllabus PDFIMEI: 355686052799688No ratings yet
- MJC 2015 H2 J1 Math Promos QuestionsDocument7 pagesMJC 2015 H2 J1 Math Promos QuestionsAlxNo ratings yet
- 2013 - 2014 H2 Maths JJC Promo SolnsDocument11 pages2013 - 2014 H2 Maths JJC Promo SolnsLionel Torres LeeNo ratings yet
- VJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 pagesVJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- 2006 AJC H2 Maths Promo - QuestionsDocument6 pages2006 AJC H2 Maths Promo - QuestionsniveumaNo ratings yet
- 2015 HCI Prelim Paper 2 SolutionsDocument13 pages2015 HCI Prelim Paper 2 SolutionsnasyrahNo ratings yet
- 2012 SH1 H2 Math CT Revison Package SolutionsDocument89 pages2012 SH1 H2 Math CT Revison Package SolutionsAnnabel Seah0% (1)
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document22 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document7 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlong0% (1)
- Acjc h2 Maths p1 QN PaperDocument6 pagesAcjc h2 Maths p1 QN Papervincesee85No ratings yet
- 2014 - DHS - Prelim Paper 2Document7 pages2014 - DHS - Prelim Paper 2Ng Shu QingNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document10 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- TPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesTPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- 2010 AJC H2 Math Promo With AnswersDocument8 pages2010 AJC H2 Math Promo With AnswersCindy KrisnadiNo ratings yet
- 2006 AJC H2 MY SolnDocument9 pages2006 AJC H2 MY Solnjunie9201No ratings yet
- Nyjc h2 Math p2 SolutionDocument11 pagesNyjc h2 Math p2 SolutionjimmytanlimlongNo ratings yet
- Term 3 Week 6 Revision Exercises - Statistics Suggested SolutionsDocument5 pagesTerm 3 Week 6 Revision Exercises - Statistics Suggested SolutionsWen Berry JiahuiNo ratings yet
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesFrom EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesNo ratings yet
- Section B AnsDocument7 pagesSection B AnsjimmytanlimlongNo ratings yet
- Which of The Following Equations Is Correct? (A) 8 J 2 KG × 4 M/s (B) 8 J 2 KG × (2 M/S) (C) 8 J 2 KG × 2 (M/S) (D) 8 J 2 KG × 4 M/sDocument1 pageWhich of The Following Equations Is Correct? (A) 8 J 2 KG × 4 M/s (B) 8 J 2 KG × (2 M/S) (C) 8 J 2 KG × 2 (M/S) (D) 8 J 2 KG × 4 M/sjimmytanlimlongNo ratings yet
- VJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument4 pagesVJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- RI JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRI JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- VJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 pagesVJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- TPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesTPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- J1 Lecture - Technology Part 1 - 2aDocument8 pagesJ1 Lecture - Technology Part 1 - 2ajimmytanlimlongNo ratings yet
- TJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument12 pagesTJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2013 NJC H2 Econs Paper 2 (Answers)Document34 pages2013 NJC H2 Econs Paper 2 (Answers)jimmytanlimlongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- TPJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument13 pagesTPJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2Document15 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2jimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document7 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1Document18 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1jimmytanlimlongNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document6 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- NJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument10 pagesNJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document7 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlong0% (1)
- PJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document10 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1Document8 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document11 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document22 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document10 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument9 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- HA With Active Data Guard 18cDocument26 pagesHA With Active Data Guard 18camartinbNo ratings yet
- Common PhrasesDocument31 pagesCommon PhrasesĐịnh NguyễnNo ratings yet
- Phys2 Ch2 Heat Temp Law0Document56 pagesPhys2 Ch2 Heat Temp Law0Trung Trần100% (1)
- Sig Wave HeightDocument2 pagesSig Wave HeightPaul OnionsNo ratings yet
- Equilibrium Constant: Gibbs Free Energy and Equilibrium Constant Le Chatelier's PrincipleDocument2 pagesEquilibrium Constant: Gibbs Free Energy and Equilibrium Constant Le Chatelier's Principlerb rbmonteNo ratings yet
- Linde EN Ds t14 t16 t18 t20 1155 en B 0522 ViewDocument6 pagesLinde EN Ds t14 t16 t18 t20 1155 en B 0522 ViewNadeem AhmedNo ratings yet
- What Caused The Accident at The Sayano - Shushenskaya Hydroelectric Power Plant (SSHPP) : A Seismologist 'S Point of ViewDocument8 pagesWhat Caused The Accident at The Sayano - Shushenskaya Hydroelectric Power Plant (SSHPP) : A Seismologist 'S Point of ViewStefan FleancuNo ratings yet
- Effect of Oxygen On Surface Tension of Liquid Ag-Sn AlloysDocument5 pagesEffect of Oxygen On Surface Tension of Liquid Ag-Sn AlloysBurak ÖZBAKIRNo ratings yet
- Ai Regents at Random WorksheetsDocument242 pagesAi Regents at Random WorksheetsSmita NagNo ratings yet
- 329 1011 1 PBDocument12 pages329 1011 1 PBTasya ArwieNo ratings yet
- Activity Number-1-Measurement-Conversion-of-Units-and-Error-AnalysisDocument2 pagesActivity Number-1-Measurement-Conversion-of-Units-and-Error-AnalysisJohn OliquianoNo ratings yet
- 3rd Quarter Activity SheetDocument3 pages3rd Quarter Activity SheetMa. Teresa BajaoNo ratings yet
- AFFF FoamDocument2 pagesAFFF Foamkalimutu2010No ratings yet
- TM-11-5855-246-10 An PAS 7 Thermal ViewerDocument105 pagesTM-11-5855-246-10 An PAS 7 Thermal ViewerArmySGTNo ratings yet
- Chemtotal Labs Pvt. LTD.: D.Col - XCDDocument1 pageChemtotal Labs Pvt. LTD.: D.Col - XCDDeepak CharanNo ratings yet
- Data Sheet 6ES7516-3FN01-0AB0: General InformationDocument9 pagesData Sheet 6ES7516-3FN01-0AB0: General InformationMarko VadasNo ratings yet
- SILICA Xilinx Zynq ZedBoard Vivado Workshop Ver1.0Document61 pagesSILICA Xilinx Zynq ZedBoard Vivado Workshop Ver1.0Chinavenkateswararao GNo ratings yet
- C18 ACERT 448bkW PDFDocument5 pagesC18 ACERT 448bkW PDFAndre KellerNo ratings yet
- Sysmex SEED Platelet Detection and The Importance of A Reliable CountDocument7 pagesSysmex SEED Platelet Detection and The Importance of A Reliable CountMuhammad Khoirut TNo ratings yet
- High-Resolution Spectroscopic Analysis of Four Unevolved Barium StarsDocument29 pagesHigh-Resolution Spectroscopic Analysis of Four Unevolved Barium Starsl2j89zxwNo ratings yet
- Hardware Design & Simulation of Advanced Traffic LightDocument16 pagesHardware Design & Simulation of Advanced Traffic LightAnimesh ShrotriaNo ratings yet
- Towers of HanoiDocument16 pagesTowers of HanoiBharadwaj KasturiNo ratings yet
- SIMSCI Component Data Input ManualDocument152 pagesSIMSCI Component Data Input Manualarmando0212-1100% (1)
- Oblique CollisionDocument8 pagesOblique Collisionaqeeel777100% (1)
- CSAT, SSC, IBPS Test PaperDocument3 pagesCSAT, SSC, IBPS Test PapersmargeduNo ratings yet
- Consumption Calculation of Vehicles Using OBD DataDocument17 pagesConsumption Calculation of Vehicles Using OBD DataCuleanu_007No ratings yet
- TraceCERT, CRM Solutions For ICP, AAS, and ICDocument12 pagesTraceCERT, CRM Solutions For ICP, AAS, and ICalvin gunadiNo ratings yet
AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2
AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2
Uploaded by
jimmytanlimlongOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2
AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2
Uploaded by
jimmytanlimlongCopyright:
Available Formats
1
Solutions to MYCT H2 Math Paper 2 with markers comments
Qn Solutions
1 In a systematic sampling, all the users are assigned a unique number from 1 and
18500. A random number between 1 and 185 inclusive is chosen initially. This user is
chosen and the next 185
th
resident is chosen until 100 residents are chosen.
A stratified sampling gives a representative sample of the population as the opinions
of the game may differ according to age groups.
2 Let X be the random variable denoting the number of marks scored by a candidate.
If
2
(78.1,15.2 ) X N , then
P( 100) 0.0748 X > =
i.e. around 7.5% of the student cohort will score above 100 marks if the random variable X is
following a Normal distribution of mean 78.1 and std dev 15.2. This is unrealistic as students
cannot score more than 100 marks.
Since n is large, by CLT,
2
15.2
78.1,
60
X N
approximately.
P(80.0 85.0) 0.166 X < < =
3(i) p =35
P (a randomly chosen component is faulty)
=
( )( ) ( )( ) 0.35 0.08 0.65 0.05 +
=0.0605
3(ii) f(p) = P( component supplied by A / faulty )
=
P(faulty component supplied by A)
P(faulty)
=
( )
( ) ( )
0.08
100
0.08 0.05
100
p
+
p
100
p
100
=
0.08 0.08
0.08 5 0.05 0.03 5
p p
p p p
=
+ +
(shown)
( )
( ) ( )
( )
( )
'
2
2
0.03 5 0.08 0.08 0.03
f
0.03 5
0.4
0.03 5
p p
p
p
p
+
=
+
=
+
2
Qn Solutions
For 0 p 100 ,
( )
'
f p >0
as p increases,
( ) f p increases.
( ) f p is a strictly increasing function.
i.e. when the company buys a larger percentage of its electronic components from
supplier A, the probability of a randomly chosen faulty component is supplied by A
increases.
4(i) Using the symmetrical properties of the normal distribution,
The mean of the distribution =
150 250
200
2
+
=
Let X be the random variable denoting the mass of an orange sold in the supermarket.
2
(200, )
P( 250) 0.1
50
P( ) 0.1
50
1.28155 39.0
X N
X
Z
> =
> =
= =
4(ii) Let Y be the random variable denoting the total mass of a small bag.
Let W be the random variable denoting the total mass of a large bag.
2
1 2 1 2
2
1 2
(5(200),5(39 )) (1000,7605)
(2(1000),2(7605)) (2000,15210)
(10(200),10(39 )) (2000,15210)
(0,30420)
Y N Y N
Y Y N Y Y N
W N W N
Y Y W N
+ +
1 2 1 2
P(| | 300) P( 300 300) 0.915 Y Y W Y Y W + < = < + < =
4(iii)
1 2
1 2
0.001( ) (2,0.01521)
0.0012( ) (2.4,0.021902)
0.001( ) 0.0012( ) ( 0.4,0.037112)
Y Y N
W N
Y Y W N
+
+
1 2
P(0.001( ) 0.0012( ) 0) 0.981 Y Y W + < =
5 (a)(i) no. of arrangements =5! X 7! =604800
(ii)
no. of arrangements =
9
P
3
x 8! =20321280
3
Qn Solutions
(iii) No of ways of dividing the people into 3 groups of 3 and
1 group of 2
=
11 8 5 2
3 3 3 2
3!
C C C C
=15400
(b) Treat man and his wife as 1 unit.
arrange 4 units +3 elderly man +1 empty seat in a circle.
No of arrangements =(8-1)! X (2!)
4
=80640
6(i)
6(ii)
Let X be the mass of the component of the electrical product and be the mean mass
of the component.
To test H
0
: = 12
vs H
1
: 12
Since population variance is known and X follows a normal distribution, we use a Z-
test.
Test statistic , Z =
12
~ (0,1)
X
N
n
Use a 2-tailed test at 5% level, ie reject Ho if p <0.05
Using G.C. with 12.28 x = , n =60 ; =1.005 , p =0.0309 <0.05 .
We reject Ho and conclude that there is sufficient evidence at 5% level to dispute the
factory owners claim.
To test H
0
: = 12
vs H
1
: <12
Since sample size is small and population variance is unknown, we use a t-test.
Test statistic, T =
12
~ (19)
X
t
s
n
From the sample, n =20 , s
2
=
20
(1.03) 1.0842
19
=
For the owners claim to be accepted reject H
0
ie reject Ho if T <-1.729
4
Qn Solutions
6(iii)
12
1.729
1.0842
20
x
< x < 11.6 ( 3 s.f.)
For part (ii), the conclusion is to reject H
0
i.e. T
cal
will lie in the rejection region.
Since the population variance is said to be known and equals to s
2
. A Z-test will be
carried out and Z
cal
=T
cal
(since s = )
From the diagram, we can conclude that there is still sufficient evidence to support
the owners claim that the mean mass is less than 12 grams at 5% level of
significance.
Alternatively,
Z-test is to be used since population variance is known.
From part (ii),
cal
12
T = 1.729
20
x
s
< (to reject Ho)
Since s = ,
cal cal
12
= T 1.729
20
x
Z
= <
At 5% significance level,
c
Z 1.6448 =
cal
1.729 1.6448 Z < < ( to reject Ho)
There is still sufficient evidence to support the owners claim that the mean mass is
less than 12 grams at 5% level of signifance.
7(i) Let X be the number of telephone calls received by a call centre in a 4-min interval, ie X
~ Po(12).
P(X > 10 ) = 1 P(X 10) =0.653
N(0,1)
t(19)
5
Qn Solutions
7(ii) Let Y be no of calls received at the call centre in n seconds,
Y ~Po
3
60
n
, ie Y ~Po
20
n
Given P ( Y 1) <0.1
20
1 0.1
20
n
n
e
+ <
Sketch y =
20
1 0.1
20
x
x
e
+
.
From G.C., for y <0 x >77.8 x =78
The shortest length of time required =n =78 secs.
7(iii) Let W be the no of calls received at the call centre in a 10-hr interval , ie W ~Po
( 1800 )
Since =1800 >10 W ~N ( 1800, 1800 ) approx
P( W >1850 ) =P ( W >1850.5 ) by continuity correction
=0.11696 =0.117
7(iv) P(manpower shortage | busy day) =0.15
P(manpower shortage) =0.15 (0.11696) =0.017544
Let S be the no of days with manpower shortage in 30 randomly chosen working days of
10 hours , S ~B( 30, 0.017544)
P( S <2 ) =P(S 1) =0.903
You might also like
- BMC Helix IT Service Management Deployment 22.1.06: Technical DocumentationDocument486 pagesBMC Helix IT Service Management Deployment 22.1.06: Technical DocumentationSupria GeraNo ratings yet
- Lesson Three Hair AppointmentDocument10 pagesLesson Three Hair AppointmentHassanNo ratings yet
- MJC JC2 H2 Maths 2012 Year End Exam Paper 2 Solutions PDFDocument10 pagesMJC JC2 H2 Maths 2012 Year End Exam Paper 2 Solutions PDFRyan LeeNo ratings yet
- 2016-Acjc-Promo-Scan (9758)Document22 pages2016-Acjc-Promo-Scan (9758)Simon AngNo ratings yet
- 2016 NJC H2 Maths PromoDocument18 pages2016 NJC H2 Maths Promomadhih123No ratings yet
- 2009 NJC SH2 H2 Mathematics Prelim Paper 2 SolutionsDocument21 pages2009 NJC SH2 H2 Mathematics Prelim Paper 2 SolutionsNicholas ChoyNo ratings yet
- CJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesCJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2007 Paper 2 Chemistry: Topic: Introduction To Organic ChemistryDocument11 pages2007 Paper 2 Chemistry: Topic: Introduction To Organic ChemistrysaffronNo ratings yet
- 2009 RI Prelims Chem H2 P3 AnsDocument7 pages2009 RI Prelims Chem H2 P3 AnsJasonNo ratings yet
- VJC h2 Math p2 SolutionsDocument4 pagesVJC h2 Math p2 Solutionsjimmytanlimlong100% (1)
- NJC h2 Math p2 Annex BDocument2 pagesNJC h2 Math p2 Annex BjimmytanlimlongNo ratings yet
- CJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesCJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- RI H2 Maths 2013 Prelim P1 SolutionsDocument13 pagesRI H2 Maths 2013 Prelim P1 Solutionsnej200695100% (1)
- 2014 H2 Maths Prelim Papers - HCI P2 Solution PDFDocument14 pages2014 H2 Maths Prelim Papers - HCI P2 Solution PDFcherylhzy100% (1)
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document10 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2015 JC2 H2 Maths Victoria Junior College PDFDocument33 pages2015 JC2 H2 Maths Victoria Junior College PDFVu Quang MinhNo ratings yet
- ACJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument6 pagesACJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2019 Y5 Promo Revision (Sem1 Topics)Document10 pages2019 Y5 Promo Revision (Sem1 Topics)Sarah RahmanNo ratings yet
- AJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document3 pagesAJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- Nyjc h2 Math p1 SolutionDocument10 pagesNyjc h2 Math p1 SolutionjimmytanlimlongNo ratings yet
- IJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document8 pagesIJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- 2012 ACJC Prelim H2 Math SolnDocument15 pages2012 ACJC Prelim H2 Math Solnckhowh_23284524667% (3)
- Sajc 2010 Prelim Math p1 SolnDocument10 pagesSajc 2010 Prelim Math p1 SolnAh XiuNo ratings yet
- 2007 IJC PrelimDocument23 pages2007 IJC PrelimWen LongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document10 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- IJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document8 pagesIJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- Teorema Limit, Satu Sisi, Apit, Trigonometri&Tak HinggaDocument117 pagesTeorema Limit, Satu Sisi, Apit, Trigonometri&Tak HinggaSari IndahNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document11 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- NJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument10 pagesNJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1Document18 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1jimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2Document15 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2jimmytanlimlongNo ratings yet
- JC 1 H2 Maths Promo Practice Paper 1Document6 pagesJC 1 H2 Maths Promo Practice Paper 1brianfletcher182No ratings yet
- TJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument12 pagesTJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- 2014 H2 Maths Prelim Papers - NJC P1 SolutionDocument13 pages2014 H2 Maths Prelim Papers - NJC P1 Solutioncherylhzy0% (4)
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document7 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document10 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongNo ratings yet
- CJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument5 pagesCJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument9 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- Ri h2 Math p2 SolutionsDocument11 pagesRi h2 Math p2 SolutionsjimmytanlimlongNo ratings yet
- ACJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 pagesACJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- RI JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRI JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1Document8 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1jimmytanlimlongNo ratings yet
- AJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 pagesAJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongNo ratings yet
- 2012 A Level H2 Chemistry Paper 2 Modified For New Syllabus PDFDocument10 pages2012 A Level H2 Chemistry Paper 2 Modified For New Syllabus PDFIMEI: 355686052799688No ratings yet
- MJC 2015 H2 J1 Math Promos QuestionsDocument7 pagesMJC 2015 H2 J1 Math Promos QuestionsAlxNo ratings yet
- 2013 - 2014 H2 Maths JJC Promo SolnsDocument11 pages2013 - 2014 H2 Maths JJC Promo SolnsLionel Torres LeeNo ratings yet
- VJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 pagesVJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- 2006 AJC H2 Maths Promo - QuestionsDocument6 pages2006 AJC H2 Maths Promo - QuestionsniveumaNo ratings yet
- 2015 HCI Prelim Paper 2 SolutionsDocument13 pages2015 HCI Prelim Paper 2 SolutionsnasyrahNo ratings yet
- 2012 SH1 H2 Math CT Revison Package SolutionsDocument89 pages2012 SH1 H2 Math CT Revison Package SolutionsAnnabel Seah0% (1)
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document22 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document7 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlong0% (1)
- Acjc h2 Maths p1 QN PaperDocument6 pagesAcjc h2 Maths p1 QN Papervincesee85No ratings yet
- 2014 - DHS - Prelim Paper 2Document7 pages2014 - DHS - Prelim Paper 2Ng Shu QingNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document10 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- TPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesTPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- 2010 AJC H2 Math Promo With AnswersDocument8 pages2010 AJC H2 Math Promo With AnswersCindy KrisnadiNo ratings yet
- 2006 AJC H2 MY SolnDocument9 pages2006 AJC H2 MY Solnjunie9201No ratings yet
- Nyjc h2 Math p2 SolutionDocument11 pagesNyjc h2 Math p2 SolutionjimmytanlimlongNo ratings yet
- Term 3 Week 6 Revision Exercises - Statistics Suggested SolutionsDocument5 pagesTerm 3 Week 6 Revision Exercises - Statistics Suggested SolutionsWen Berry JiahuiNo ratings yet
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesFrom EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesNo ratings yet
- Section B AnsDocument7 pagesSection B AnsjimmytanlimlongNo ratings yet
- Which of The Following Equations Is Correct? (A) 8 J 2 KG × 4 M/s (B) 8 J 2 KG × (2 M/S) (C) 8 J 2 KG × 2 (M/S) (D) 8 J 2 KG × 4 M/sDocument1 pageWhich of The Following Equations Is Correct? (A) 8 J 2 KG × 4 M/s (B) 8 J 2 KG × (2 M/S) (C) 8 J 2 KG × 2 (M/S) (D) 8 J 2 KG × 4 M/sjimmytanlimlongNo ratings yet
- VJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument4 pagesVJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- RI JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRI JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- VJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument4 pagesVJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- TPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesTPJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- J1 Lecture - Technology Part 1 - 2aDocument8 pagesJ1 Lecture - Technology Part 1 - 2ajimmytanlimlongNo ratings yet
- TJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument12 pagesTJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- 2013 NJC H2 Econs Paper 2 (Answers)Document34 pages2013 NJC H2 Econs Paper 2 (Answers)jimmytanlimlongNo ratings yet
- RVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument6 pagesRVHS JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- TPJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument13 pagesTPJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2Document15 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 2jimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document7 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- SRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1Document18 pagesSRJC JC 2 H2 Maths 2011 Mid Year Exam Questions Solutions Paper 1jimmytanlimlongNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2Document6 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 2jimmytanlimlongNo ratings yet
- NJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument10 pagesNJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- PJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document7 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlong0% (1)
- PJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document10 pagesPJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- NYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1Document5 pagesNYJC JC 2 H2 Maths 2011 Mid Year Exam Question Paper 1jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1Document8 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 1jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2Document11 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 2jimmytanlimlongNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument14 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Document22 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNo ratings yet
- MJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2Document10 pagesMJC JC 2 H2 Maths 2011 Mid Year Exam Questions Paper 2jimmytanlimlongNo ratings yet
- JJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsDocument9 pagesJJC JC 2 H2 Maths 2011 Mid Year Exam QuestionsjimmytanlimlongNo ratings yet
- HA With Active Data Guard 18cDocument26 pagesHA With Active Data Guard 18camartinbNo ratings yet
- Common PhrasesDocument31 pagesCommon PhrasesĐịnh NguyễnNo ratings yet
- Phys2 Ch2 Heat Temp Law0Document56 pagesPhys2 Ch2 Heat Temp Law0Trung Trần100% (1)
- Sig Wave HeightDocument2 pagesSig Wave HeightPaul OnionsNo ratings yet
- Equilibrium Constant: Gibbs Free Energy and Equilibrium Constant Le Chatelier's PrincipleDocument2 pagesEquilibrium Constant: Gibbs Free Energy and Equilibrium Constant Le Chatelier's Principlerb rbmonteNo ratings yet
- Linde EN Ds t14 t16 t18 t20 1155 en B 0522 ViewDocument6 pagesLinde EN Ds t14 t16 t18 t20 1155 en B 0522 ViewNadeem AhmedNo ratings yet
- What Caused The Accident at The Sayano - Shushenskaya Hydroelectric Power Plant (SSHPP) : A Seismologist 'S Point of ViewDocument8 pagesWhat Caused The Accident at The Sayano - Shushenskaya Hydroelectric Power Plant (SSHPP) : A Seismologist 'S Point of ViewStefan FleancuNo ratings yet
- Effect of Oxygen On Surface Tension of Liquid Ag-Sn AlloysDocument5 pagesEffect of Oxygen On Surface Tension of Liquid Ag-Sn AlloysBurak ÖZBAKIRNo ratings yet
- Ai Regents at Random WorksheetsDocument242 pagesAi Regents at Random WorksheetsSmita NagNo ratings yet
- 329 1011 1 PBDocument12 pages329 1011 1 PBTasya ArwieNo ratings yet
- Activity Number-1-Measurement-Conversion-of-Units-and-Error-AnalysisDocument2 pagesActivity Number-1-Measurement-Conversion-of-Units-and-Error-AnalysisJohn OliquianoNo ratings yet
- 3rd Quarter Activity SheetDocument3 pages3rd Quarter Activity SheetMa. Teresa BajaoNo ratings yet
- AFFF FoamDocument2 pagesAFFF Foamkalimutu2010No ratings yet
- TM-11-5855-246-10 An PAS 7 Thermal ViewerDocument105 pagesTM-11-5855-246-10 An PAS 7 Thermal ViewerArmySGTNo ratings yet
- Chemtotal Labs Pvt. LTD.: D.Col - XCDDocument1 pageChemtotal Labs Pvt. LTD.: D.Col - XCDDeepak CharanNo ratings yet
- Data Sheet 6ES7516-3FN01-0AB0: General InformationDocument9 pagesData Sheet 6ES7516-3FN01-0AB0: General InformationMarko VadasNo ratings yet
- SILICA Xilinx Zynq ZedBoard Vivado Workshop Ver1.0Document61 pagesSILICA Xilinx Zynq ZedBoard Vivado Workshop Ver1.0Chinavenkateswararao GNo ratings yet
- C18 ACERT 448bkW PDFDocument5 pagesC18 ACERT 448bkW PDFAndre KellerNo ratings yet
- Sysmex SEED Platelet Detection and The Importance of A Reliable CountDocument7 pagesSysmex SEED Platelet Detection and The Importance of A Reliable CountMuhammad Khoirut TNo ratings yet
- High-Resolution Spectroscopic Analysis of Four Unevolved Barium StarsDocument29 pagesHigh-Resolution Spectroscopic Analysis of Four Unevolved Barium Starsl2j89zxwNo ratings yet
- Hardware Design & Simulation of Advanced Traffic LightDocument16 pagesHardware Design & Simulation of Advanced Traffic LightAnimesh ShrotriaNo ratings yet
- Towers of HanoiDocument16 pagesTowers of HanoiBharadwaj KasturiNo ratings yet
- SIMSCI Component Data Input ManualDocument152 pagesSIMSCI Component Data Input Manualarmando0212-1100% (1)
- Oblique CollisionDocument8 pagesOblique Collisionaqeeel777100% (1)
- CSAT, SSC, IBPS Test PaperDocument3 pagesCSAT, SSC, IBPS Test PapersmargeduNo ratings yet
- Consumption Calculation of Vehicles Using OBD DataDocument17 pagesConsumption Calculation of Vehicles Using OBD DataCuleanu_007No ratings yet
- TraceCERT, CRM Solutions For ICP, AAS, and ICDocument12 pagesTraceCERT, CRM Solutions For ICP, AAS, and ICalvin gunadiNo ratings yet