Professional Documents
Culture Documents
Quasi-Static Undrained Expansion of A Cylindrical Cavity in Clay in The Presence of Shaft Friction and Anisotropic Initial Stresses
Quasi-Static Undrained Expansion of A Cylindrical Cavity in Clay in The Presence of Shaft Friction and Anisotropic Initial Stresses
Uploaded by
LTE002Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Quasi-Static Undrained Expansion of A Cylindrical Cavity in Clay in The Presence of Shaft Friction and Anisotropic Initial Stresses
Quasi-Static Undrained Expansion of A Cylindrical Cavity in Clay in The Presence of Shaft Friction and Anisotropic Initial Stresses
Uploaded by
LTE002Copyright:
Available Formats
619
Quasi-static undrained expansion of a cylindrical cavity in clay in
the presence of shaft friction and anisotropic initial stresses
C. Sagaseta
a,
, G.T. Houlsby
b
, H.J. Burd
b
a
Department of Materials and Ground Engineering, University of Cantabria, Av. de Los Castros, s/n, 39005 Santander, Spain
b
Department of Engineering Science, University of Oxford, Oxford, UK
Abstract
Solutions for cylindrical cavity expansion in an innite incompressible medium are presented. The solutions account for
large strain in both the plastic and elastic regions. They account also for the inuence of an axial shear stress at the surface
of the cavity, and also for the possibility of unequal vertical and horizontal stresses. The solutions are presented principally
in closed-form, although they make some use of a series solution and of integrals which must be evaluated numerically.
The solutions have application to the determination of the stresses around axially loaded piles and around in-situ testing
devices such as penetrometers.
Keywords: Cavity expansion; Elastoplastic; Incompressible material; Analytical solution; Von Mises; Large strains;
Eulerian formulation
1. Introduction
In the paper we present an analytical solution for the
quasi-static expansion of a cylindrical cavity in an incom-
pressible elastoplastic soil. There are many other published
solutions of the problem, either in closed form (for instance
[1]) or numerically [2,4]. The novelty here lies in the fact
that we account for the possibility of (a) shaft friction
in the axial direction, and (b) in-situ horizontal stress not
necessarily equal to in-situ vertical stress.
The soil is treated as incompressible elasticperfect
plastic, with the Von Mises yield condition. The proper-
ties are dened by the parameters: G (incompressibility
requires that Poissons ratio = 0.5), and s
u
= (
1
3
)/2
in triaxial conditions (
2
=
3
). The shear modulus may be
expressed by dening the rigidity index, I
r
=G/s
u
.
The cavity is vertical, and its radius, a, expands steadily,
starting from zero. The expansion of a cavity with -
nite initial radius a
0
can be recovered from the solutions
given below, simply by tracking the stresses at radius
r =
_
a
2
0
a
2
. As stated above, the analysis concentrates on
the inuence of the following factors, not considered in the
previous solutions:
Corresponding author. Tel.: +34 (942) 201813; Fax: +34 (942)
201821; E-mail: sagasetac@unican.es
The action of a longitudinal uniform shear traction at
the cavity wall,
a
. This is relevant for driven piles and
for cone pressuremeters.
An anisotropic, but uniform, initial state of stresses
(
v0
=
h0
).
Large strains in both the plastic and elastic zones (usu-
ally, small strains are assumed in the elastic region).
The rst two points imply the presence of shear stresses,
additional to the effect of the cavity expansion. This has an
inuence on the extent of the plastic zone.
2. Problem formulation
The problem is formulated in cylindrical coordinates
(r, , z). The kinematic description of the motion, taking the
cavity radius, a, as the time variable, is fully dened by the
conditions of axial symmetry, the innite length of cylinder
and soil incompressibility:
r =
_
r
2
0
+a
2
_
1/2
=
0
z = z
0
+w(r, a)
(1)
The cavity axis, OZ, is not a principal direction, so the
deformation is not strictly one of plane strain. However, the
condition remains that all the variables are constant with z,
and that the axial strain rate is zero.
2003 Elsevier Science Ltd. All rights reserved.
Computational Fluid and Solid Mechanics 2003
K.J. Bathe (Editor)
620 C. Sagaseta et al. / Second MIT Conference on Computational Fluid and Solid Mechanics
The components of the strain rate tensor are:
rr
=
v
r
r
=
r
_
r
a
_
=
a
r
2
=
v
r
r
=
1
r
_
r
a
_
=
a
r
2
zz
=
v
z
z
=
z
_
z
a
_
=0
rz
=
_
v
z
r
+
v
r
z
_
=
r
_
z
a
_
z
_
r
a
_
=
a
_
z
r
_
=
a
_
w
r
_
(2)
where (v
r
=r/a; v
=0; v
z
=z/a) are the soil veloci-
ties.
The strain rates are related to the material derivatives of
the stress through the elasticplastic constitutive equations:
i j
=
e
i j
+
p
i j
=C
i j kl
d
kl
da
+
f
i j
(3)
where f =0 is the Von Mises yield condition:
f =(
rr
)
2
+(
zz
)
2
+(
zz
rr
)
2
+6
2
rz
8s
2
u
(4)
From dimensional analysis, the stresses must depend
on the radial coordinate r only through the ratio =
a/r. Hence, the material derivatives of the stresses can be
expressed in terms of the spatial radial derivative as:
d
i j
da
=
i j
r
r
a
+
i j
a
=
_
a
r
r
a
_
i j
r
(5)
The equilibrium equations are:
r
r
+
r
=0
rz
r
+
rz
r
=0
(6)
We assume that the shear stress at the inner boundary is
constant, so that the boundary conditions are:
for r =a :
rz
=
a
for r =:
r
=
=
h0
;
z
=
v0
;
rz
=0
(7)
3. Solution procedure
The stresses are decomposed into their isotropic ( p) and
deviatoric (s
i j
) parts:
i j
= p
i j
+s
i j
(8)
where
i j
is the Kronecker delta (unit tensor). In the plastic
zone, the following variables are used, generalized from
Lodes parameters:
s
rr
=
4
3
s
u
cos sin
_
+
6
_
s
=
4
3
s
u
cos sin
_
6
_
s
zz
=
4
3
s
u
cos cos
s
rz
=
2
3
s
u
sin
(9)
The equations for stresses and strains in the vertical and
horizontal directions are only partially coupled. The veloci-
ties and strain rates in any horizontal plane, (v
r
, v
,
rr
,
)
are dened from Eqs. (1) and (2). On the other hand, the
corresponding shear stress
rz
is fully dened by the second
equilibrium Eq. (6), both in the elastic and plastic zones.
This decoupling allows a stepped solution. First, the
shear stress,
rz
, is obtained from the second equilibrium
Eq. (6). Then, the system is integrated for the normal
stresses, starting from the innite boundary, and assuming
elastic behavior, until the condition f =0 is reached. This
determines the position of the elasticplastic boundary,
=
R
. Then, the stresses and strain rates are integrated in
the plastic zone, and the normal pressure at the cavity wall
is obtained.
4. Results
In the presentation of results, use is made of the follow-
ing non-dimensional parameters:
, shaft shear factor (0 1):
rz(r=a)
=
a
=
2
3
s
u
(10)
0
, initial stress ratio:
0
=
v0
h0
2 s
u
(11)
4.1. Stresses in the elastic zone
We express the stresses in the form:
rr
= G () +
h0
= G
_
() +2ln(1
2
)
_
+
h0
zz
= G
_
() +ln(1
2
)
_
+
v0
rz
=
a
(12)
where the function () can be expressed as a power
series:
() =
_
1
n
2
2n
_
=
2
+
1
4
4
+
1
9
6
+. . . (13)
Note that this solution differs very slightly from the
conventional solution in the elastic region in which small
strains are assumed.
C. Sagaseta et al. / Second MIT Conference on Computational Fluid and Solid Mechanics 621
4.2. Elasticplastic boundary ( =
R
)
The position of the boundary is given by:
ln
_
1
2
R
_
=
2
1
I
r
_
1
2
0
2
R
(14)
For =0 this reduces to:
2
R
=1exp
_
1
I
r
_
1
2
0
_
(15)
4.3. Stresses in the plastic zone
Deviatoric stresses:
The deviatoric stresses may be expressed by the follow-
ing functions which should be substituted into Eq. (9):
sin =
1+sin
cos
=
1+sin
R
cos
R
_
cos +cos
a
cos
R
+cos
a
cos
R
cos
a
cos cos
a
_
3
2
Ir
1
cos a
(16)
For =0 these reduce to:
=0
1+sin
cos
=
1+sin
R
cos
R
_
1
2
R
1
2
_
3
2
Ir
(17)
and for =1:
sin =
1+sin
cos
=
1+sin
R
cos
R
exp
_
3 I
r
_
1
cos
R
1
cos
__
(17
)
Isotropic pressure:
The mean stress is expressed as:
p = p
R
4
3
s
u
_
cos sin
_
+
6
_
cos
R
sin
_
R
+
6
__
+
4
3
s
u
R
1
cos sin d
(18)
In all the expressions, the subscripts R and a mean the
values at the elasticplastic boundary ( =
R
) and at the
cavity wall ( = 1), respectively. The integral in Eq. (18)
needs to be evaluated numerically as a closed-form integra-
tion is not available.
Wall pressure:
The pressure at the cavity wall,
a
, is the value of
rr
for = 1. For the case of isotropic initial stresses (
0
=0)
this can be obtained as a closed form expression:
a
=
h0
+G (
R
) +
4
3
s
u
_
_
1
2
_
1
2
2
R
ln
R
ln
1+
1
2
1+
_
1
2
2
R
_
(19)
which, in the absence of shaft friction ( =0) reduces to:
a
=
h0
+G (
R
)
4
3
s
u
ln
R
Expanding
R
(15) and (13) into power series and taking
only their rst term, leads to:
2
R
=
2
1
I
r
=
h0
+
2
3
s
u
_
1+ln
3
2
I
r
_
(20)
which coincides with the existing solutions for small strains
in the elastic region.
4.4. Velocities and strain rates
The velocities and strain rates in the horizontal plane
(v
r
, v
,
rr
,
) are dened from Eqs. (1) and (2). The ver-
tical velocity, v
z
, becomes innite, due to a logarithmic
term which necessarily appears in two-dimensional elastic-
ity problems containing resultant forces [3]. This is usually
overcome by assuming that the displacements vanish at
some arbitrary distance, such as the magical radius used
by Randolph and Wroth [4].
The velocity v
z
and the shear strain rate,
rz
, are given
by:
v
z
=
w
a
rz
=
a
_
w
r
_ (21)
with:
w =w
e
+w
p
w
e
(elastic) =
a
a
I
r
_
ln
r
m
r
1
6
_
2
m
_
_
w
p
(plastic)
_
_
=0 if <
R
=
r=r
_
r=R
a=ar
_
a=0
p
rz
da dr if
R
(22)
p
rz
=
1
I
r
2
a
2
_
1
2
0
_
3/2
_
r
2
a
2
_
r
3
_
r
2
2
a
2
_
1
2
0
__
+8
a
2
_
1
2
0
_
1/2
sin
r
2
_
r
2
2
a
2
_
1
2
0
__
1/2
In the above expressions, r
m
(
m
= a/r
m
) is a magical
radius (in theory, r
m
, but in practice it can be taken
as some appropriate multiple of the axial length over which
622 C. Sagaseta et al. / Second MIT Conference on Computational Fluid and Solid Mechanics
the cavity expansion occurs). The integration for w
p
must
be performed numerically. The limit a
r
is the value of the
cavity radius a for which the plastic zone reaches r, the
point of calculation of w
p
, dened by the condition:
a
2
r
r
2
=
2
r
=1exp
_
1
I
r
_
_
1
2
0
__
1
2
2
r
_
_
(23)
Acknowledgements
The main part of the work presented herein was per-
formed during the visit of the rst author to the University
of Oxford, partially sponsored by a BritishSpanish Joint
Research project.
References
[1] Gibson RE, Anderson WF. In situ measurement of soil
properties with the pressuremeter. Civil Eng Pub Works Rev
1978;56:615618.
[2] Randolph MF, Wroth CP. An analysis of the deformation of
vertically loaded piles. J Geotech Eng Div ASCE 1978;104
(GT12):14651488.
[3] Strack OE. Analytic Solutions of Elastic Tunneling Problems.
Ph.D. Thesis, Delft University of Technology, Delft Univer-
sity Press, 2002.
[4] Yu HS, Houlsby, GT. Finite cavity expansion in dilatant
soils: loading analysis. Gotechnique 1991;41(2):173183.
You might also like
- Doku - Pub - Fluid Mechanics and Hydraulics Revised Edition Gillesania PDFDocument249 pagesDoku - Pub - Fluid Mechanics and Hydraulics Revised Edition Gillesania PDFKeith Garrido0% (1)
- Activity Series LabDocument6 pagesActivity Series LabJonathan_Khan7100% (4)
- Ansi Asabe Ep545 Mar1995 (r2010)Document10 pagesAnsi Asabe Ep545 Mar1995 (r2010)StephanNo ratings yet
- Little Bit Lame Equation PDFDocument20 pagesLittle Bit Lame Equation PDFAhmad FauzanNo ratings yet
- Chapter 6Document4 pagesChapter 6newrome76No ratings yet
- DYNAMIC ANALYSIS OF LAMINATED CROSS-PLY PANEL UNDER LOCALIZED MOMENT by Ali Be IglooDocument6 pagesDYNAMIC ANALYSIS OF LAMINATED CROSS-PLY PANEL UNDER LOCALIZED MOMENT by Ali Be Iglooantony1993No ratings yet
- LabDocument9 pagesLabKin Wai HongNo ratings yet
- Static SolutionDocument7 pagesStatic SolutionCarlos Andres Moyano BuitragoNo ratings yet
- Linear Elastic Stress AnalysisDocument27 pagesLinear Elastic Stress AnalysisUr FriendNo ratings yet
- 2006 Int Ansys Conf 47Document27 pages2006 Int Ansys Conf 47Maria TnsNo ratings yet
- On The Shape Factor For The Maximum Pressure of The Undercut Groove FormDocument8 pagesOn The Shape Factor For The Maximum Pressure of The Undercut Groove FormVanesh KumarNo ratings yet
- MIT3 11F99 AiryDocument14 pagesMIT3 11F99 AiryADITYANo ratings yet
- Introduction To Fracture Mechanics Introduction To Fracture MechanicsDocument56 pagesIntroduction To Fracture Mechanics Introduction To Fracture MechanicsShiba Narayan SahuNo ratings yet
- D13 PDFDocument7 pagesD13 PDFHồ ThắngNo ratings yet
- Object-Oriented Nonlinear Finite Element Programming: A PrimerDocument17 pagesObject-Oriented Nonlinear Finite Element Programming: A PrimerBosslucianNo ratings yet
- Theory of PlasticityDocument49 pagesTheory of PlasticityGoutham Burra0% (1)
- Cylinders: Many ApplicationsDocument15 pagesCylinders: Many ApplicationsdearsaswatNo ratings yet
- MECH3310 Mechanics of Solids 2: The University of SydneyDocument8 pagesMECH3310 Mechanics of Solids 2: The University of SydneyJim LettermanNo ratings yet
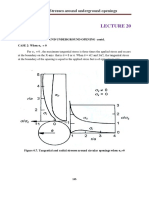
- Shear Stresses Around Circular Cylindrical OpeningsDocument14 pagesShear Stresses Around Circular Cylindrical OpeningsBeny AbdouNo ratings yet
- KossaDocument5 pagesKossaWilliam Gomez ZabaletaNo ratings yet
- Plane Stress TransformDocument24 pagesPlane Stress Transformsandrock92No ratings yet
- Dundee Final HDRDocument13 pagesDundee Final HDRFranco BrownNo ratings yet
- Thick Walled Cylinders (Plane Stress)Document16 pagesThick Walled Cylinders (Plane Stress)Alvaro FabianNo ratings yet
- MECH3310 Mechanics of Solids 2: The University of SydneyDocument8 pagesMECH3310 Mechanics of Solids 2: The University of SydneyJim LettermanNo ratings yet
- Isotropic Linear Elastic Stress ConcentrationDocument19 pagesIsotropic Linear Elastic Stress ConcentrationIoan-Lucian StanNo ratings yet
- Stresses Around UndergroundDocument41 pagesStresses Around UndergroundNhật LêNo ratings yet
- MECH3310 Mechanics of Solid 2: The University of SydneyDocument7 pagesMECH3310 Mechanics of Solid 2: The University of SydneyJim LettermanNo ratings yet
- Singular Behaviour at The End of A Tensile Crack in A Hardening MaterialDocument19 pagesSingular Behaviour at The End of A Tensile Crack in A Hardening MaterialPeterNo ratings yet
- Lecture 20Document10 pagesLecture 20فردوس سليمانNo ratings yet
- Hamilton 1966Document6 pagesHamilton 1966alex thomasNo ratings yet
- Radial Fingering in A Hele-Shaw Cell: Ladhyx Internship Report, October 3 - December 23, 2011Document31 pagesRadial Fingering in A Hele-Shaw Cell: Ladhyx Internship Report, October 3 - December 23, 2011okochaflyNo ratings yet
- Homework 1 Solutions: 1 Jackson 1.3Document5 pagesHomework 1 Solutions: 1 Jackson 1.3ahsanqauNo ratings yet
- HW1Document8 pagesHW1nirre87No ratings yet
- CH - 6 - Elastic-Plastic Fracture MechanicsDocument28 pagesCH - 6 - Elastic-Plastic Fracture MechanicsSerawit Tadesse100% (1)
- SeismicDocument21 pagesSeismicsoumyasssNo ratings yet
- X.0.hooke's LawDocument32 pagesX.0.hooke's LawSuresh SjNo ratings yet
- Ex2 - SolutionDocument5 pagesEx2 - SolutionNicolas SalibaNo ratings yet
- Boundary Layer NotesDocument17 pagesBoundary Layer NotesgarystevensozNo ratings yet
- Mechanic of Solids: Stress and StrainDocument28 pagesMechanic of Solids: Stress and StrainLuis VarelaNo ratings yet
- 1 SI Ciarletta 2013Document16 pages1 SI Ciarletta 2013Benjamin OlowuNo ratings yet
- Radial Viscous Flow Between Two Parallel Annular PlatesDocument12 pagesRadial Viscous Flow Between Two Parallel Annular PlatesKyi Htin PawNo ratings yet
- StressDocument25 pagesStressHoac Chu KenNo ratings yet
- Long-Wave Instability in Double-Diffusive Marangoni ConvectionDocument18 pagesLong-Wave Instability in Double-Diffusive Marangoni ConvectionvarmaprasadNo ratings yet
- A Comparative Study On Failure Pressure Estimations of Unflawed Cylindrical VesselsDocument14 pagesA Comparative Study On Failure Pressure Estimations of Unflawed Cylindrical VesselsBrighton JohnNo ratings yet
- Thick Wall CylinderDocument7 pagesThick Wall Cylinderchuckhsu1248No ratings yet
- Analysis of Stress and Strain in A Rotating Disk Mounte PDFDocument26 pagesAnalysis of Stress and Strain in A Rotating Disk Mounte PDFJigneshNo ratings yet
- Jose P. S. Lemos and Francisco S. N. Lobo - Plane Symmetric Traversable Wormholes in An Anti-De Sitter BackgroundDocument14 pagesJose P. S. Lemos and Francisco S. N. Lobo - Plane Symmetric Traversable Wormholes in An Anti-De Sitter BackgroundRtpomNo ratings yet
- Torsion of Orthotropic Bars With L-Shaped or Cruciform Cross-SectionDocument15 pagesTorsion of Orthotropic Bars With L-Shaped or Cruciform Cross-SectionRaquel CarmonaNo ratings yet
- Plane-Strain State of An Elastoplastic Body With A Crack Under Mixed-Mode LoadingDocument8 pagesPlane-Strain State of An Elastoplastic Body With A Crack Under Mixed-Mode LoadingmshameliNo ratings yet
- Static Equilibrium: M M M F F FDocument41 pagesStatic Equilibrium: M M M F F FINMENo ratings yet
- Main Course Non Linear DynamicsDocument24 pagesMain Course Non Linear Dynamicsjuan_saldíaNo ratings yet
- Exam 3Document8 pagesExam 3methmadNo ratings yet
- Alternating Method Applied To Analyse Mode-III Fracture Problems With Multiple Cracks in An Infinite DomainDocument11 pagesAlternating Method Applied To Analyse Mode-III Fracture Problems With Multiple Cracks in An Infinite DomainNguyen Ba DungNo ratings yet
- Mechanics of CompositesDocument20 pagesMechanics of CompositesKamineni JagathNo ratings yet
- Chapter 7 Two-Dimensional FormulationDocument18 pagesChapter 7 Two-Dimensional FormulationHk Lorilla QuongNo ratings yet
- O-H. Kim, Y.C. Kim: 2. TheoryDocument4 pagesO-H. Kim, Y.C. Kim: 2. Theoryjainrakeshj4987No ratings yet
- Muh 29 6 4 0506 7Document8 pagesMuh 29 6 4 0506 7Sneh YadavNo ratings yet
- Book 3 Contact MechanicsDocument17 pagesBook 3 Contact MechanicsPablo FiniNo ratings yet
- Mathematical Analysis 1: theory and solved exercisesFrom EverandMathematical Analysis 1: theory and solved exercisesRating: 5 out of 5 stars5/5 (1)
- A-level Maths Revision: Cheeky Revision ShortcutsFrom EverandA-level Maths Revision: Cheeky Revision ShortcutsRating: 3.5 out of 5 stars3.5/5 (8)
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Commensurabilities among Lattices in PU (1,n). (AM-132), Volume 132From EverandCommensurabilities among Lattices in PU (1,n). (AM-132), Volume 132No ratings yet
- ZH - 2005 RCDocument99 pagesZH - 2005 RCLTE002No ratings yet
- Soil WashingDocument19 pagesSoil WashingLTE002No ratings yet
- Biomass To Ethanol ProcessDocument132 pagesBiomass To Ethanol ProcessLTE002No ratings yet
- High PerformanceDocument3 pagesHigh PerformanceLTE002No ratings yet
- Cal Methodology - Energy Saving - Electrical - HouseholdDocument15 pagesCal Methodology - Energy Saving - Electrical - HouseholdLTE002No ratings yet
- Simulation of High-Speed FillingDocument13 pagesSimulation of High-Speed FillingLTE002No ratings yet
- Trigger Sprayer Dynamic Systems ModelDocument5 pagesTrigger Sprayer Dynamic Systems ModelLTE002No ratings yet
- 49 Structure Porosity of Flocculated ADDocument8 pages49 Structure Porosity of Flocculated ADLTE002No ratings yet
- Paper - 84 Magnetic FormingDocument8 pagesPaper - 84 Magnetic FormingLTE002No ratings yet
- Paper - 5 Noise MinimizationDocument5 pagesPaper - 5 Noise MinimizationLTE002No ratings yet
- Support System Design of Power House and Transformer Caverns in DDocument5 pagesSupport System Design of Power House and Transformer Caverns in Dvikalp1982No ratings yet
- Basic in ElectricityDocument26 pagesBasic in ElectricityShang Divina EbradaNo ratings yet
- Bibo TroxDocument8 pagesBibo TroxFelipeTinelNo ratings yet
- Boiler Materials For USC Plants IJPGC 2000Document22 pagesBoiler Materials For USC Plants IJPGC 2000pawanumarji1100% (1)
- Worksheet 2 PH Measurement and Buffer PreparationDocument15 pagesWorksheet 2 PH Measurement and Buffer PreparationAkeysha CarreonNo ratings yet
- Spiral Ducts AccessoriesDocument14 pagesSpiral Ducts AccessoriesRifki FajarNo ratings yet
- Ahmed, Tarek - Reservoir Engineering HandbookDocument2 pagesAhmed, Tarek - Reservoir Engineering HandbookJenzelNo ratings yet
- Comparitive of Waterproofing WorkDocument12 pagesComparitive of Waterproofing WorkReshik KannanNo ratings yet
- Polymers: Application of Gelatin in Food Packaging: A ReviewDocument19 pagesPolymers: Application of Gelatin in Food Packaging: A ReviewLeycoline AlmrenNo ratings yet
- Mechanics of Material Lab ReportDocument47 pagesMechanics of Material Lab ReportMuhammad Junaid Tabassum50% (2)
- Textile Raw Material-II Course Code: Tex2101: Basic Concept On Textile FibreDocument63 pagesTextile Raw Material-II Course Code: Tex2101: Basic Concept On Textile FibreHrs ShihabNo ratings yet
- 03jul201502074415 PDFDocument6 pages03jul201502074415 PDFSaran KumarNo ratings yet
- Auger Electron Spectroscopy (AES) LabDocument1 pageAuger Electron Spectroscopy (AES) LabElliott Stone0% (1)
- Tripathiper2004 PDFDocument12 pagesTripathiper2004 PDFKim Vill NierraNo ratings yet
- Cortec - Vapor Corrosion Inhibitors in Novel Applications in The Middle East - Khalil Abed, Usma JacirDocument6 pagesCortec - Vapor Corrosion Inhibitors in Novel Applications in The Middle East - Khalil Abed, Usma JacirmindbagNo ratings yet
- Chapter 8: Band Theory of Solids Concept of Free Electron Theory: Hour 1Document25 pagesChapter 8: Band Theory of Solids Concept of Free Electron Theory: Hour 1Vivek kapoorNo ratings yet
- Homework Assignment No. 9: Problem SetDocument5 pagesHomework Assignment No. 9: Problem SetspritdummyNo ratings yet
- Ground Improvement PDFDocument31 pagesGround Improvement PDFGeorge KinaNo ratings yet
- Basic Construction Training Manual Swiss Red Cross Skat FoundationDocument92 pagesBasic Construction Training Manual Swiss Red Cross Skat FoundationAnonymous M0tjyWNo ratings yet
- Experimental Innovations in Surface Science: John T. Yates JRDocument637 pagesExperimental Innovations in Surface Science: John T. Yates JRAmar kumar100% (1)
- PA Asia Product LineDocument2 pagesPA Asia Product LineDuc NguyenNo ratings yet
- Filler Electrode QtyDocument2 pagesFiller Electrode QtyRajeev KumarNo ratings yet
- Eavemaster Fascia SoffitDocument8 pagesEavemaster Fascia SoffitJackyNo ratings yet
- Parts List 21dxs288rd BR MR MBDocument5 pagesParts List 21dxs288rd BR MR MBAhmadNo ratings yet
- Mod 7Document47 pagesMod 7mkpq100% (1)
- Solid ElementsDocument6 pagesSolid ElementsAbhay YadavNo ratings yet