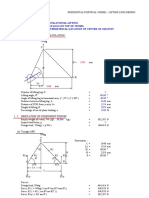
MIL-STD-209J Lifting Calculations

These calculations determine the design loads, ultimate loads, sling lengths and sling angles
required to meet MIL-STD-209J. The data generated from these calculations should be used for
design purposes and for testing. There are two steps for these calculations. STEP ONE is to
determine the load factor and STEP TWO is to calculate the loads and sling angles.
STEP ONE - Determine load factor
The load factor is either 2.3 for crane lift only, or a higher value for crane lift and helicopter lift.
Fill in the red numbers for the external air transport weight (EATWT) and the maximum projected
frontal area (MPFA) numbers for your item. The program will calculate the EATWT/MPFA ratio
and the load factor for helicopter and crane lift. Choose the correct load factor that is
appropriate for the item's transport requirements.
EATWT= 10,000 pounds
MPFA= 34.50 square feet
EATWT/MPFA= 289.86 pounds/sq ft
Helicopter and
Crane Lift OR
Crane Lift
Only
Load Factor for STEP TWO = 3.2 2.3
Choose the correct Load Factor and enter here: 2.3
STEP TWO - Calculate loads and sling angles
Please enter the numbers shown in red for your specific piece of equipment. See figure 1 for examples
of each of the variables.
Figure 1
GW 37,090 pounds
Lf 130.5 inches
Lr 188.5 inches
Hf 47.6 inches
Hr 47.6 inches
Da 57.8 inches
Db 55.6 inches
Dc 55.6 inches
Dd 57.8 inches
Results of the MI L-STD-209J Lifting Calculations
Location Angle of sling Sling Leg Design Limit Ultimate
with the vertical Length (in) Load (lb) Load (lb)
(degrees)
Front Left, A
36 239 30,583 45,875
Front Right, B
36 239 31,674 47,511
Rear Right, C
54 239 30,372 45,559
Rear Left, D
54 239 29,369 44,053
Apex height =
18.2 feet
(Must be less than 24 feet)
Below are the equations and formulas used for arriving at the values in the above table.
The equations are exactly the same as in Appendix B of MIL-STD-209J.
Determine b, the angle of the plane of the provisions with respect to the horizontal, and Lxy.
Hr-Hf=D= 0.0 inches
L=Lf+Lr= 319.0 inches
TAN(b)=D/L; b=TAN^-1(D/L)= 0.0 degrees
COS(b)=L/Lxy; Lxy=L/COS(b) 319.0 inches
Determine h
L
and S (these are constant for all slings).
Dab = (Da + Db)/2 = 56.7 inches
Dcd = (Dc + Dd)/2 = 56.7 inches
To solve for h
L
, we have three equations and three unknowns.
h
L
= SQRT(Dab^2 + Lx^2)
h
L
= SQRT(Dcd^2 + Ly^2)
Lx = Lxy - Ly
By substituting the third equation into the first equation, we can solve for Ly.
h
L
= SQRT(Dab^2 + (Lxy - Ly)^2) = SQRT(Dcd^2 + Ly^2)
Ly = (Dab^2 - Dcd^2 + Lxy^2)/2Lxy = 159.5 inches
And then solve for Lx and h
L.
Lx = Lxy - Ly = 159.5 inches
h
L
= SQRT(Dab^2 + Lx^2) = 169.3 inches
SA is set to 45 degrees to determine the sling length for a single apex sling assembly.
COS(45) = h
L
/S; S = h
L
/COS(45)= 239.4 inches = 19.9 feet
If S is shorter than 12 feet, the sling length for an equal length single apex sling assembly is set to 12 feet.
This is most likely the shortest size of slings that will be available in the field to lift an item.
Sling length of all slings, S, used for remainder of calculations: 19.9 feet 239.4
COS(SA)=h
L
/S; SA = COS^-1(h
L
/S) = 45.0 degrees
Determine ha, hb, hc, hd, hat, hbt, hct, hdt, and K.
ha = SQRT(Lf^2 + Da^2) = 142.7 inches
hb = SQRT(Lf^2 + Db^2) = 141.9 inches
hc = SQRT(Lr^2 + Dc^2) = 196.5 inches
hd = SQRT(Lr^2 + Dd^2) = 197.2 inches
COS(b) = ha/hat;hat = ha/COS(b) = 142.7 inches
The same equation can be applied to the other provisions.
COS(b) = hb/hbt;hbt = hb/COS(b) = 141.9 inches
COS(b) = hc/hct;hct = hc/COS(b) = 196.5 inches
COS(b) = hd/hdt;hdt = hd/COS(b) = 197.2 inches
K^2 = S^2 + hat^2 - 2ShatCOS(SA)
K = SQRT(S^2 + hat^2 - 2ShatCOS(SA)) = 171.3 inches
Determine VA, the angle of the slings with the vertical when the equipment is lifted.
hat^2=S^2 + K^2 - 2SKCOS(VAa);
VAa = COS
-1
(S^2 + K^2 - hat^2/2SK) = 36.1 degrees
VAb = COS
-1
(S^2 + K^2 - hbt^2/2SK) = 35.8 degrees
VAc = COS
-1
(S^2 + K^2 - hct^2/2SK) = 54.2 degrees
VAd = COS
-1
(S^2 + K^2 - hdt^2/2SK) = 54.4 degrees
Determine the vertical force component, V, at each provision.
Va = Lr/(Lr + Lf)*Db/(Da + Db)*GW = 10,746 pounds
Vb = Lr/(Lr + Lf)*Da/(Da + Db)*GW = 11,171 pounds
Vc = Lf/(Lr + Lf)*Dd/(Dc + Dd)*GW = 7,734 pounds
Vc = Lf/(Lr + Lf)*Dc/(Dc + Dd)*GW = 7,439 pounds
Determine the static load, R, for each sling leg.
Ra = Va/COS(VAa) = 13,297 pounds
Rb = Vb/COS(VAa) = 13,771 pounds
Rc = Vc/COS(VAc) = 13,205 pounds
Rd = Vd/COS(VAd) = 12,769 pounds
Determine the required design limit load, T.
Ta = Ra*LF = 30,583 pounds
Tb = Rb*LF = 31,674 pounds
Tc = Rc*LF = 30,372 pounds
Td = Rd*LF = 29,369 pounds
Determine the required design limit load, U.
Ua = Ta*1.5 = 45,875 pounds
Ub = Ta*1.5 = 47,511 pounds
Uc = Ta*1.5 = 45,559 pounds
Ud = Ta*1.5 = 44,053 pounds
Determine the apex height, Ha.
Ht = TAN(b)(ha) = 0.0 inches
Ha = Hf + Ht + K 218.9 inches = 18.2 feet