Professional Documents
Culture Documents
How Large Is Large?: Ani Adhikari and Philip Stark
How Large Is Large?: Ani Adhikari and Philip Stark
Uploaded by
tamleduc1810dn0 ratings0% found this document useful (0 votes)
18 views23 pagesThe document discusses how the normal approximation for the binomial distribution depends on the number of trials and the probability of success on each trial. It notes that with 1000 trials and a probability of success of 1/1000, the distribution is not close to normal. However, with 10,000 trials from the same probability distribution, the distribution begins to approach normal. It advises checking that expected value plus or minus 3 standard errors does not produce impossible values before applying the normal approximation to a binomial distribution.
Original Description:
Original Title
lec4.5
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThe document discusses how the normal approximation for the binomial distribution depends on the number of trials and the probability of success on each trial. It notes that with 1000 trials and a probability of success of 1/1000, the distribution is not close to normal. However, with 10,000 trials from the same probability distribution, the distribution begins to approach normal. It advises checking that expected value plus or minus 3 standard errors does not produce impossible values before applying the normal approximation to a binomial distribution.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
0 ratings0% found this document useful (0 votes)
18 views23 pagesHow Large Is Large?: Ani Adhikari and Philip Stark
How Large Is Large?: Ani Adhikari and Philip Stark
Uploaded by
tamleduc1810dnThe document discusses how the normal approximation for the binomial distribution depends on the number of trials and the probability of success on each trial. It notes that with 1000 trials and a probability of success of 1/1000, the distribution is not close to normal. However, with 10,000 trials from the same probability distribution, the distribution begins to approach normal. It advises checking that expected value plus or minus 3 standard errors does not produce impossible values before applying the normal approximation to a binomial distribution.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
You are on page 1of 23
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
How large is large?
1000 independent, repeated S/F trials
p = 1/1000 chance of success on a single trial
Probability distribution of the number of successes
binomial n = 1000, p = 1/1000 = 0.001
Sum of 1000 draws at random with replacement from 1 1 999 0
expected value of the number of successes = 1000 0.001 = 1
SE of the number of successes =
1000 0.001 0.999 = 0.9995
Not normal!
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 1 / 1
The probability histogram
1000 trials, p = 1/1000
number of successes
p
r
o
b
a
b
i
l
i
t
y
0 1 2 3 4 5 6
0
.
0
0
.
1
0
.
2
0
.
3
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 2 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
When the box is far from symmetric
1000 seems large
but 1 1 999 0 is such an uneven distribution that 1000 draws iare
not enough for the CLT to kick in
What if we made 10,000 draws from the same box?
expected value of the number of successes = 10, 000 0.001 = 10
SE of the number of successes =
10, 000 0.001 0.999 = 3.16
Normal?
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 3 / 1
Approaching normal
10,000 trials, p = 1/1000
number of successes
p
r
o
b
a
b
i
l
i
t
y
0 5 10 15 20 25 30
0
.
0
0
0
.
0
4
0
.
0
8
0
.
1
2
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 4 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice: Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice: Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice: Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice:
Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice: Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice: Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
Bad boxes
It takes lots of draws for the probability histogram for the sum to
start looking normal if the contents of the box
are far from symmetric, for example skewed
have a histogram that has gaps
Practical advice: Calculate expected value 3SE and check whether you
are hitting impossible values for the variable.
If you are, then dont use the normal approximation.
If you are not, then go ahead, but be aware that it still might not be
great . . .
Ani Adhikari and Philip Stark Statistics 2.2X Lecture 4.5 5 / 1
You might also like
- Classifying Rational and Irrational WorksheetDocument3 pagesClassifying Rational and Irrational Worksheetapi-32704152433% (3)
- Tutorial4 solutionsEE3110Document6 pagesTutorial4 solutionsEE3110doss PrakashNo ratings yet
- Chi-Square Test: by DR - RM SaxenaDocument18 pagesChi-Square Test: by DR - RM SaxenaRakesh Mohan SaxenaNo ratings yet
- Chi SquareDocument18 pagesChi SquaremanduramNo ratings yet
- Exponents: by Monica YuskaitisDocument24 pagesExponents: by Monica YuskaitisVu Thi Hai AnhNo ratings yet
- Scientific Notation Powerpoint PDFDocument18 pagesScientific Notation Powerpoint PDFKatheeja MusatheekNo ratings yet
- Materi 2.2 Introduction - To - CombinatoricDocument7 pagesMateri 2.2 Introduction - To - CombinatoricFiqri NugrahaNo ratings yet
- 1stQ.2.2 Significant Figures and Scientific NotationDocument25 pages1stQ.2.2 Significant Figures and Scientific NotationRaiden Gabriel LontokNo ratings yet
- Introduction To ProbabilityDocument61 pagesIntroduction To ProbabilityJocelyn G. TamaresNo ratings yet
- ProbabilityDocument126 pagesProbabilityRaca DesuNo ratings yet
- Lecture Set 5Document32 pagesLecture Set 5Dirt KickNo ratings yet
- Basic Mathematical Skills-AARDocument44 pagesBasic Mathematical Skills-AARsaud ahmedNo ratings yet
- 3.1 Random Sampling PDFDocument36 pages3.1 Random Sampling PDFMariel EnglisNo ratings yet
- ScientificNotationDocument19 pagesScientificNotationCoco BelarminoNo ratings yet
- Chapter 10 - CountingDocument55 pagesChapter 10 - CountingashNo ratings yet
- Problem Solving Chapter 3 - Math in The Modern WorldDocument50 pagesProblem Solving Chapter 3 - Math in The Modern WorldGregorio Gamboa Maniti IINo ratings yet
- Math4-Q1-W7 PresentationDocument41 pagesMath4-Q1-W7 PresentationSherina LinangNo ratings yet
- 2.0final Sig Figs and Sci NotationDocument39 pages2.0final Sig Figs and Sci NotationPeter Pan100% (1)
- Skills Nursing Numeracy Essentials PDFDocument8 pagesSkills Nursing Numeracy Essentials PDFmarco_alcalá_1No ratings yet
- Y 456 STR 1Document32 pagesY 456 STR 1Rula ShakrahNo ratings yet
- Sample Papers For Class 7 Maths Mock 2Document17 pagesSample Papers For Class 7 Maths Mock 2Jubin JainNo ratings yet
- UNIT 3 Lessons 2 and 3 SCIENTIFIC NOTATION AND SIGNIFICANT FIGURESDocument23 pagesUNIT 3 Lessons 2 and 3 SCIENTIFIC NOTATION AND SIGNIFICANT FIGURESSheena GomezNo ratings yet
- Math Lessons: Presented By: Shea Iris C. SamonteDocument18 pagesMath Lessons: Presented By: Shea Iris C. SamonteSheaNo ratings yet
- Lecture 9 - Discrete Structure - Discrete Probability - Part 1Document23 pagesLecture 9 - Discrete Structure - Discrete Probability - Part 1bedoamr75No ratings yet
- Statistics Skittles Project Part 4Document2 pagesStatistics Skittles Project Part 4api-385652369No ratings yet
- Math ReportDocument23 pagesMath Reportjp gonzalesNo ratings yet
- Module 3 Problem Solving and ReasoningDocument16 pagesModule 3 Problem Solving and ReasoningRafa LandayanNo ratings yet
- 5th Grade Division: Mrs. BerishDocument197 pages5th Grade Division: Mrs. BerishCj ReyesNo ratings yet
- Chap 5Document52 pagesChap 5august mayNo ratings yet
- Scientific NotationDocument15 pagesScientific NotationEusebio Torres TatayNo ratings yet
- Probability GBRDocument36 pagesProbability GBRWeb BooksNo ratings yet
- Binomial dist-BUDocument52 pagesBinomial dist-BUMuqadas HakimNo ratings yet
- Fermi Coaches Clinic PresentationDocument29 pagesFermi Coaches Clinic Presentationvitoribeiro90No ratings yet
- The Normal Binomial and Poisson DistributionsDocument25 pagesThe Normal Binomial and Poisson DistributionsDeepak RanaNo ratings yet
- Math 4-Q4-Module-7Document15 pagesMath 4-Q4-Module-7Clever Lane MontessoriNo ratings yet
- Encode MathDocument30 pagesEncode MathJerome OcampoNo ratings yet
- Student Workbook - Unit 3 - DecimalsDocument14 pagesStudent Workbook - Unit 3 - Decimalsapi-232099327No ratings yet
- Math 7 GRADE 7 DAY ONLYDocument9 pagesMath 7 GRADE 7 DAY ONLYERRALYN PEÑAFLORIDANo ratings yet
- SCINOTATIONDocument16 pagesSCINOTATIONZachary Gardaya100% (1)
- Decimals: Multiply and Divide by 10, 100 and 1000: Year 5: Week 2, Day 1Document12 pagesDecimals: Multiply and Divide by 10, 100 and 1000: Year 5: Week 2, Day 1helena100% (1)
- Accuracy and Precision Significant Figures Density MeasurementsDocument36 pagesAccuracy and Precision Significant Figures Density MeasurementsAngelhyka Bacagan RebollidoNo ratings yet
- Chi-Square Test PresentationDocument28 pagesChi-Square Test Presentationpchimanshu27No ratings yet
- Clifford Bridge 2023-SATs Parents Guide FinalDocument20 pagesClifford Bridge 2023-SATs Parents Guide FinalLoredana DalabanNo ratings yet
- FormulaeDocument24 pagesFormulaeanuragNo ratings yet
- The Normal Binomial and Poisson DistributionsDocument25 pagesThe Normal Binomial and Poisson Distributionss_mahesNo ratings yet
- Question Bank Class - VIII MathsDocument18 pagesQuestion Bank Class - VIII Mathsgvkumar.awsNo ratings yet
- STAT1Document41 pagesSTAT1Diana Marie MedinaNo ratings yet
- Teaching Secondary Mathematics: Learning Through Investigation: Focus On Chance and VariabilityDocument26 pagesTeaching Secondary Mathematics: Learning Through Investigation: Focus On Chance and VariabilityPiNo ratings yet
- Lesson 8 - Part 2: Scientific NotationDocument12 pagesLesson 8 - Part 2: Scientific NotationmisterreidNo ratings yet
- Concept: Mathematics 4 - Quarter 1 Week 2Document9 pagesConcept: Mathematics 4 - Quarter 1 Week 2ferlyn marasiganNo ratings yet
- Topic 4 Scientific NotationsDocument13 pagesTopic 4 Scientific Notationswohaib.riaz.wr17No ratings yet
- Parent LetterDocument2 pagesParent Letterapi-318953940No ratings yet
- Scientific NotationDocument22 pagesScientific NotationMikah Zabaljauregui100% (1)
- Funmath Module 4 - Scientific Notation and Significant FiguresDocument7 pagesFunmath Module 4 - Scientific Notation and Significant FiguresRonelle San buenaventuraNo ratings yet
- Year 5 Maths RevisionDocument26 pagesYear 5 Maths RevisionWilsonBrendan100% (5)
- 1 Preflop FinalizedDocument321 pages1 Preflop FinalizedR RiNo ratings yet
- Inductive and Deductive Reasoning Logic PuzzleDocument5 pagesInductive and Deductive Reasoning Logic PuzzleNeri SangalangNo ratings yet
- BS UNIT 2 Probability New PDFDocument62 pagesBS UNIT 2 Probability New PDFSherona ReidNo ratings yet
- Teaching Secondary Mathematics: Learning Through Investigation: Focus On Chance and VariabilityDocument26 pagesTeaching Secondary Mathematics: Learning Through Investigation: Focus On Chance and Variabilitybonifacio gianga jrNo ratings yet
- GCSE Maths Revision: Cheeky Revision ShortcutsFrom EverandGCSE Maths Revision: Cheeky Revision ShortcutsRating: 3.5 out of 5 stars3.5/5 (2)
- Mathematical Snacks: A Collection of Interesting Ideas to Fill Those Spare MomentsFrom EverandMathematical Snacks: A Collection of Interesting Ideas to Fill Those Spare MomentsNo ratings yet
- PopDocument15 pagesPoptamleduc1810dnNo ratings yet
- Lilll::ls'i I ?? Q EDocument8 pagesLilll::ls'i I ?? Q Etamleduc1810dnNo ratings yet
- MTechDocument11 pagesMTechtamleduc1810dnNo ratings yet
- SS Note-Making PDFDocument2 pagesSS Note-Making PDFtamleduc1810dnNo ratings yet
- Planner Trimester 1 2014Document4 pagesPlanner Trimester 1 2014tamleduc1810dnNo ratings yet
- SS Exam Day StrategiesDocument2 pagesSS Exam Day Strategiestamleduc1810dnNo ratings yet
- REF MLA ReferencingDocument4 pagesREF MLA Referencingtamleduc1810dnNo ratings yet
- Exam Day Planner PDFDocument1 pageExam Day Planner PDFtamleduc1810dnNo ratings yet
- Daily Subject Planner: To Do List': Date Due Subject Notes DoneDocument1 pageDaily Subject Planner: To Do List': Date Due Subject Notes Donetamleduc1810dnNo ratings yet
- REF Traditional FootnotingDocument4 pagesREF Traditional Footnotingtamleduc1810dnNo ratings yet
- A Test-All TopicsDocument10 pagesA Test-All Topicstamleduc1810dnNo ratings yet
- 11 LogarithmsDocument4 pages11 Logarithmstamleduc1810dnNo ratings yet
- 15 SetTheoryDocument2 pages15 SetTheorytamleduc1810dnNo ratings yet
- Concave ProgrammingDocument10 pagesConcave Programmingcharles luisNo ratings yet
- COMSOLDocument20 pagesCOMSOLatpeplowNo ratings yet
- Lec 5Document19 pagesLec 5Б. НандинбилэгNo ratings yet
- Aliaksei Maistrou - Finite Element Method DemystifiedDocument26 pagesAliaksei Maistrou - Finite Element Method DemystifiedsuyogbhaveNo ratings yet
- Heaviside's Operators and Contour IntegralsDocument28 pagesHeaviside's Operators and Contour IntegralsalpcruzNo ratings yet
- S5 L07 Shear Stresses in Thin-Walled BeamDocument11 pagesS5 L07 Shear Stresses in Thin-Walled BeamduplexprabuNo ratings yet
- GATE Control Systems by KanodiaDocument97 pagesGATE Control Systems by Kanodiakaran11364% (11)
- Chapter 7 - StabilityDocument42 pagesChapter 7 - Stabilityvenosyah devanNo ratings yet
- I V Savelyev Fundametals of Theoretical Physics Vol 1 PDFDocument425 pagesI V Savelyev Fundametals of Theoretical Physics Vol 1 PDFpfael100% (4)
- Coupling of Optical Fibers and Scattering in Fibers PDFDocument11 pagesCoupling of Optical Fibers and Scattering in Fibers PDFRenan Portela JorgeNo ratings yet
- Measures of Central TendencyDocument22 pagesMeasures of Central TendencyVickyNo ratings yet
- Phys 221 ExercisesDocument4 pagesPhys 221 ExercisesKristine Rodriguez-CarnicerNo ratings yet
- DAA Lab Ex 9,10 PDFDocument9 pagesDAA Lab Ex 9,10 PDFVarunNo ratings yet
- The Harmonic OscillatorDocument8 pagesThe Harmonic OscillatorEugenio PérezNo ratings yet
- Pontryagin's Maximum Principle: Emo TodorovDocument12 pagesPontryagin's Maximum Principle: Emo TodorovmanishNo ratings yet
- Argand Diagrams and The Polar FormDocument12 pagesArgand Diagrams and The Polar FormHassaan650No ratings yet
- NM3 Root s02Document15 pagesNM3 Root s02sori1386No ratings yet
- Math Pickup LinesDocument1 pageMath Pickup LinesAlena JosephNo ratings yet
- The Cartesian Plane: Focus OnDocument8 pagesThe Cartesian Plane: Focus Onkuanyo yoNo ratings yet
- Types and Classification of Control System Module-Christy Jane P. SanchezDocument3 pagesTypes and Classification of Control System Module-Christy Jane P. SanchezChristy Jane SanchezNo ratings yet
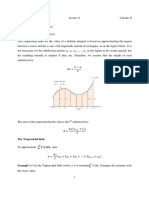
- Numerical Integration: Trapezoidal ApproximationDocument7 pagesNumerical Integration: Trapezoidal ApproximationIbrahem HadiNo ratings yet
- Circles-Ellipses-Parabolas: Chapter 12: Geometry of SpaceDocument8 pagesCircles-Ellipses-Parabolas: Chapter 12: Geometry of SpaceKhaled RafeiNo ratings yet
- Question 1 (20 Marks) : Mathematics For Technology II Sample Test - Marking Scheme Page 1 of 5Document5 pagesQuestion 1 (20 Marks) : Mathematics For Technology II Sample Test - Marking Scheme Page 1 of 5Mohammed ABDO ALBAOMNo ratings yet
- Quadratic Function Exam QuestionsDocument20 pagesQuadratic Function Exam QuestionsCho Ah YoungNo ratings yet
- Trace Class OperatorsDocument10 pagesTrace Class OperatorsJuan Jose Martinez ValladaresNo ratings yet
- 2 Dimensional Manifolds PDFDocument6 pages2 Dimensional Manifolds PDFGuifré Sánchez SerraNo ratings yet
- Properties of FunctionDocument45 pagesProperties of FunctionChristiansen Jovan TaranNo ratings yet
- Pset 1 18.06 Spring 2020 SolutionDocument2 pagesPset 1 18.06 Spring 2020 Solutionanotherser01No ratings yet