Si t e Cont e nt s

NUMERALS
Numerals Introduction
Horus Eye Fractions
Creation by numerals
Shen Ring Universe
Heh God Millions
Tadpole Proliferation
Finger Counting
Lotus Rise
Rope Geometry
Vault of Heaven
Upright Life
CONSTANTS
Creation by constants
Genesis Equations
Creation Prelude
Ark to Altar line
Ladder to heaven
King Solomon's Pi
Number perceptions
Golden ratio properties >
Golden ratio prehistory
Woman Wisdom
Constant e of growth
Outer limit circle
Temple dimensions
Matching traditions
Auspicious latitudes
Reader responses

Visit our other Sections:
Prime Patterns
Board Games
Astronomy
Medicine

Store Stuff:
Home Page
Search this site
FAQ about e-books


recoveredscience.com

We offer surprises about
and numerals and their ancient religious uses in our e-book
Ancient Creation Stories told by the Numbers
by H. Peter Aleff






The mathematics of Genesis 1

in the layout of the Jerusalem Temple


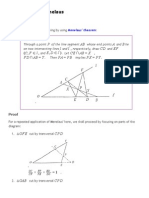
Some properties of the golden ratio phi

The geometric definition of the golden section is
that it divides a length into a larger part and a smaller
part so that the smaller part forms the same ratio with
the larger part as the larger part does with the whole.
Raster picture
.gif = 31 Kb
view vector version 25 Kb
info on vector viewing plug-in
This definition is fairly simple, but the magic starts when you add that
larger part to the previous whole because the new whole is again in the
same phi ratio to the initial whole, and that new one to the next, and so
on. Each time the new length grows out of the old in unchanged
proportion.
The same is also true for the triangles and rectangles formed from this
golden ratio, as well as for their logarithmic spirals which these form, as
shown in the picture above. It also applies to the construction of the
regular pentagon since this figure is entirely formed from golden triangles
and produces phi over and over again with the ratios between its
component lengths.
The study of phi reveals many such unusual geometrical and arithmetical
properties, and many mathematicians have written with great enthusiasm
about this extraordinary number. Some of these surprising features of phi
are illustrated in the picture above or listed in the Tables below.
A small sampling from the many unique properties of the golden
section
Phi and its reciprocal 1 / phi are the two solutions:
phi = (Root 5 + 1 ) / 2 and
1 / phi = (Root 5 1) / 2
of the equation x
2
- x - 1 = 0. These solutions are perfect mirrors that
reflect each others digit sequence after the decimal point, all the way to

FAQ about e-books
Download free e-books
Sign in for updates
Our Privacy Policy
Useful Links and Books
Rebranding
About us
email us



Footnotes :

1 Table adapted from H.E. Huntley: The
Divine Proportion -- a Study in Mathematical
Beauty, Dover Publications, New York,
1970,., page 40.
2 O. Neugebauer: The Exact Sciences in
Antiquity, 1957, edition consulted Dover,
New York, 1969, see note 9, page 25.
3 Simo Parpola: The Assyrian Tree of Life:
Tracing the Origins of Jewish Monotheism
and Greek Philosophy, Journal of Near
Eastern Studies, Volume 52, July 1993,
Number 3, pages 161-208, see note 103 on
pages 188 and 189.
4 Marshall Clagett: Ancient Egyptian
Science, Volume 2: Calendars, Clocks,
and Astronomy, American Philosophical
Society, Philadelphia, 1995, page 49, citing
Utterances 251 and 320 in which the word
for hours is determined both times by three
stars.
5 R. Bker and F. Schmeidler: ber Namen
und Identifizierung der gyptischen Dekane,
Centaurus 1984, Institute of History of
Science, Aarhus, Denmark, Vol. 27, pp. 189
to 217.

reflect each others digit sequence after the decimal point, all the way to
infinity:
phi = 1.618033988749894848204586834365....
1 / phi = 0.618033988749894848204586834365....
Phi is its own reciprocal added to
1, and adding 1 to phi is the same
as squaring it. Adding phi to its
square yields its cube; this adding
of sequential powers always
produces the next one.
1 / phi + 1 = phi
phi + 1 = phi
2
phi + phi
2
= phi
3
phi
2
+ phi
3
= phi
4
phi
n
+ phi
n+1
= phi
n+2
The same holds true for negative
powers and continues the same
way, on and on, again as in a
mirror.
1 = 1/phi + 1/phi
2
1/phi = 1/phi
2
+ 1/phi
3
1/phi
2
= 1/phi
3
+ 1/phi
4
1/phi
3
= 1/phi
4
+ 1/phi
5
Phi has also a special relationship
with the square root of 5 which is
the irrational number Root 5 =
2.236068..., derived from the
fingers of one hand that so creates
this equally versatile number.
phi + 1/phi = Root 5
1/phi = (Root 5 1) /2
phi = (Root 5 + 1) /2
phi
2
= (Root 5 + 3) /2
phi
3
= Root 5 + 2
phi
4
= Root 5 + 3 + phi
Phi and its mirroring functions
create together the first five
integers, and phi itself is the sum
of all its reciprocal powers:
1/ phi + 1/phi
2
= 1
phi + 1/phi
2
= 2
phi
2
+ 1 /phi
2
= 3
(phi + 1/phi
2
)
2
= 4
(phi + 1/phi )
2
= 5
1/phi + 1/phi
2
+ 1/phi
3
+ 1/phi
4
+ 1/phi
5
+ 1/phi
6
+ ... = phi
Each next number in the Fibonacci sequence below is formed by adding
the second last entry to the last one. As the entries grow larger, the ratios
between successive pairs of Fibonacci numbers, shown in the last row,
converge ever closer towards phi.
0+1
1
1/1
1.00
1+1
2
2/1
2.00
1+2
3
3/2
1.500
2+3
5
5/3
1.666
3+5
8
8/5
1.600
5+8
13
13/8
1.625
8+13
21
21/13
1.6154
13+21
34
34/21
1.6190
21+34
55
55/34
1.6176
34+55
89
89/55
1.6182
55+89
144
144/89
1.6180
Many modern writers have expressed amazement and delight about
these and other unique properties of this golden ratio. If any ancient
number researchers were aware of some among these astonishing
properties, they would surely have been impressed. They would also
have looked for symbolic analogies of that numbers behavior outside
the numerical domain.
These analogies are easy to find. For instance, the cycle of the moon
resembles that of the digit sequences in phi behind the decimal point as
you multiply phi with itself. These digit sequences are the same for the
odd powers of phi and their reciprocals in the bold rows below, but not
for the even powers between them.
The decimal expansion of the negative even powers is one less the
decimal digits of the corresponding positive power, so the expansion of
the even powers looks different, and the mirroring of the digits seems to
disappear in them. The successive powers of phi produce therefore a
disappear in them. The successive powers of phi produce therefore a
pattern in which they alternately display that reflection and then hide it
again, just as the moon alternately reflects the light of the sun and then
does not. This striking pattern is easy to find, and any curious ancients
who explored the powers of this constant could easily have discovered it.
Digit sequence symmetries
in positive and negative powers of phi:
phi
n
phi
1
= 1.61803398875
phi
2
= 2.61803398875
phi
3
= 4.23606797750
phi
4
= 6.85410196625
phi
5
= 11.09016994375
phi
6
= 17.94427191000
phi
7
= 29.03444185375
phi
8
= 46.97871376376
phi
9
= 76.01315561752
phi
10
= 122.9918693812
phi
11
= 199.0050249987
phi
12
= 321.9968943800
phi
13
= 521.0019193789
1 / phi
n
1/phi
1
= 0.61803398875
1/phi
2
= 0.38196601125
1/phi
3
= 0.23606797750
1/phi
4
= 0.14589803375
1/phi
5
= 0.09016994375
1/phi
6
= 0.05572809000
1/phi
7
= 0.03444185375
1/phi
8
= 0.02128623624
1/phi
9
= 0.01315561752
1/phi
10
= 0.00813061875
1/phi
11
= 0.00502499874
1/phi
12
= 0.00310562001
1/phi
13
= 0.00191937894
Phi suggests also another similarity with the moon in the radians system
of expressing angles. This system is less arbitrary than the division of a
circle into 360 degrees, and some early mathematicians could easily have
used it although we have no surviving written record of their having done
so.
In that radians system, you simply measure the rim length of the circle
section that corresponds to an angle, and you divide this length by the
radius of the circle. The 180 degrees of a half circle produce then a rim
length of pi, and a right angle is pi / 2.
In that system, the squares of the doubled sinus and cosinus for each
successive twentieth of pi are all reflected by simple functions of phi that
grow and decrease according to the progress of those pi fractions along
the circle. Together, these form the well- ordered display of quasi-
mirrored symmetries in the list below
1
. (R means here square root)
The waxing and waning functions of phi
that reflect successive twentieths of pi:
Angle(180
0
= pi)
pi / 20 = 9
0
pi / 10 = 18
0
( 2 sin)
2
of that angle
2 - R (phi+ 2) = 0.097887
1 - 1/ phi = 0.381966
( 2 cos)
2
of that angle
2 +R (phi+ 2) = 3.902113
phi + 2 = 3.618034
pi / 10 = 18
0
3 pi / 20 = 27
0
pi / 5 = 36
0
pi / 4 = 45
0
3 pi / 10 = 54
0
7 pi / 20 = 63
0
2 pi / 5 = 72
0
9 pi / 20 = 81
0
2 -R (2- 1/phi) = 0.824429
2 - 1/ phi = 1.381966
phi - 1/ phi = 1.000000
phi + 1 = 2.618034
2+R (2- 1/phi) = 3.175571
phi + 2 = 3.618034
2 +R (phi+ 2) = 3.902113
2 +R (2- 1/phi) = 3.175571
phi + 1 = 2.618034
phi - 1/ phi = 1.000000
2 - 1/ phi = 1.381966
2 -R (2- 1/phi) = 0.824429
1 - 1/ phi = 0.381966
2 -R (phi+ 2) = 0.097887
If any ancients explored such a system of measuring angles by the
periphery they enclosed, then this reflecting of pi the sun advancing
along its circuit by the waxing and waning and self- mirroring of the
corresponding phi- functions would probably also have impressed them
as clear similarities with the behavior of the moon.
The 360 degree system of measuring angles
The 360 degree system produces its own connection between phi and
the moon because an angle of 1.618... degrees has a cotangens of
35.4013. Ten times this cotangens matches the 354 calendar days in the
lunar year which was and still is used widely in the Near East.
We may dismiss such matches as accidental because degrees are an
artificial division, but the ancients would have seen that division as part
of the natural order decreed by the gods since 360 was a holy number,
six times the Great One of sixty which formed a new unit in the
Sumerian sexagesimal system.
The 360- degree system for dividing the circle is not attested in writing
until the last few centuries BCE on some Mesopotamian tablets
2
.
However, the Assyrian cultic year had long divided the annual cycle as
well as the circumference of the universe into 360 days or parts
3
. And
long before them, the Sumerians believed that the number world was
ordered by the sexagesimal system on which this division is based, so
chances are they would have applied the same order to their
surroundings.
On the other side of the Fertile Crescent, the Egyptian astronomers also
tracked circles the way we still do.
It is true that their builders measured angles only by means of the seked
which was the cotangens, or horizontal distance from the top of a
vertical cubit rod, just as roof builders today express their slopes as the
tangens, in inches of rise per foot of run.
The Egyptian skywatchers, however, had organized a band of stars
along a complete turn of the sky into 36 sections, the decans, that
succeeded each other in ten- day intervals and so matched the 36 ten-
day weeks in their 360- day civil year. This system is attested already
from Old Kingdom times by the mention of night hours in the Pyramid
from Old Kingdom times by the mention of night hours in the Pyramid
Texts
4
from about 2,300 BCE, and later coffin lids and tomb ceilings
5
were sometimes decorated with elaborate pictures of those star- clocks.
Like the Assyrian cultic year, the Egyptian civil year matched no
observable cycle but was an artifical construct with a round and
religiously significant number that also happened to come close to the
359.805 day average between the solar and lunar years and so paid equal
respect to both.
The Egyptians made up most of the difference with the actual solar year
by tacking on an extra five birthdays of the gods that were not part of
any year and did not count in the flow of time. These were considered
unlucky days, but that was a small price to pay for maintaining the
numerical harmony of the yearly cycle.
The idea of dividing cycles and circles into 360 equal parts is thus much
older than the first written documentation of the 360- degree system. It
seems therefore reasonable to assume that many ancient number
investigators may well have been aware of it, and that they could also
have noticed the numerical link it produced between the cotangens of phi
and the lunar year.
We may consider such patterns at most as curious coincidences, but the
ancient number magicians did not believe in random chance. They would
have seen these perceived similarities and symbolic identities as a sign of
deep connections between the moon and the mysterious golden ratio
which mirrored that celestial bodys behavior and produced its numbers.
In addition, they would also have taken the mirror reflections in those
digit sequences as a symbol for water, just as the tide- and fluid-
controlling moon was in many beliefs closely associated with water.
Return to the main text
Advertisement:
You can try out our http://www.pass4sure.com/CCNP-Security.html and latest
http://www.pass4sure.com/certification/cissp-study-guide.html to get high flying success in
final http://www.actualtests.com/onlinetest/lsat-practice-test.htm and
http://www.actualtests.com/onlinetest/sat-practice-test.htm exams. Our
http://www.actualtests.com/exam-642-993.htm is also a very useful tool.


Return to navigation bar Back to top About us
Our Privacy Policy Useful Links Rebranding
Contact us at recoveredscience.com
2097 Cottonwood Drive, Vineland, NJ 08361 USA
All not otherwise credited material on this site is
All not otherwise credited material on this site is
1982 to 2014 H. Peter Aleff. All rights reserved.