Professional Documents
Culture Documents
Mi 1
Mi 1
Uploaded by
mekoaaaCopyright:
Available Formats
You might also like
- Solution Manual For Modern Quantum Mechanics 2nd Edition by SakuraiDocument13 pagesSolution Manual For Modern Quantum Mechanics 2nd Edition by SakuraiRyo Kinase36% (14)
- Assignment 2F: ProjectionDocument2 pagesAssignment 2F: ProjectionGábor KölesNo ratings yet
- WORKSHEET-understanding Quadrilaterals - Class 8Document12 pagesWORKSHEET-understanding Quadrilaterals - Class 8Manoj Pandey60% (5)
- Townsend, Quantum Physics, CHAP - 3, Schodinger EqDocument24 pagesTownsend, Quantum Physics, CHAP - 3, Schodinger EqElcan DiogenesNo ratings yet
- Engineering MechanicDocument24 pagesEngineering MechanicManoj BallaNo ratings yet
- Chapter 6 - Moments of InertiaDocument20 pagesChapter 6 - Moments of InertiaLetshego Itumeleng MoahloliNo ratings yet
- Applications of Double and Triple IntegralsDocument7 pagesApplications of Double and Triple IntegralsRyan YeeNo ratings yet
- Bending Stress in Beams: Basic AssumptionsDocument9 pagesBending Stress in Beams: Basic AssumptionspidotnasirNo ratings yet
- Chapter 3.a (CG Centroid)Document21 pagesChapter 3.a (CG Centroid)LogarithemNo ratings yet
- Aplicaciones de La Integral DobleDocument91 pagesAplicaciones de La Integral DobleCristian Andres Fuentes CarbajalNo ratings yet
- MP13 Quantum Mechanics 2Document40 pagesMP13 Quantum Mechanics 2Ahmad Fikry IskandarNo ratings yet
- Jackson 8.1 Homework Problem SolutionDocument4 pagesJackson 8.1 Homework Problem SolutionDaniel GuerreroNo ratings yet
- MEG 214 - 8aDocument49 pagesMEG 214 - 8aSimiloluwa ObasaNo ratings yet
- CurveDocument19 pagesCurveSheryll de GuzmanNo ratings yet
- Lecture #19: Moments of InertiaDocument19 pagesLecture #19: Moments of InertiaAfiqah ZainuddinNo ratings yet
- Centroids and Centre of GravityDocument56 pagesCentroids and Centre of GravitydearsaswatNo ratings yet
- Chapter 6 Moment of InertiaDocument30 pagesChapter 6 Moment of Inertiaomar tahaNo ratings yet
- Nuclear PhysicsDocument11 pagesNuclear Physicsgiovanny_francisNo ratings yet
- Bending Stress of BeamsDocument18 pagesBending Stress of BeamsRambabu RNo ratings yet
- Moment of InertiaDocument15 pagesMoment of InertiamotahareshNo ratings yet
- KIX1001 - Week 9 (2023-2024)Document47 pagesKIX1001 - Week 9 (2023-2024)haqeemifarhanNo ratings yet
- University Institute of Engineering Academic Unit 3Document38 pagesUniversity Institute of Engineering Academic Unit 3Vinoth Rouge RockersNo ratings yet
- Applications of Differential EquationsDocument28 pagesApplications of Differential Equationsmaths203No ratings yet
- Quantum Field Theory Notes: Ryan D. Reece November 27, 2007Document23 pagesQuantum Field Theory Notes: Ryan D. Reece November 27, 2007jamaeeNo ratings yet
- Concentrated Forces:: Unit IV Distributed ForcesDocument11 pagesConcentrated Forces:: Unit IV Distributed Forcesbpal1970No ratings yet
- Basic Concepts:: U (1/2EI) M (X) DX U L: V And, Since W UDocument7 pagesBasic Concepts:: U (1/2EI) M (X) DX U L: V And, Since W UAberaMamoJaletaNo ratings yet
- 1.2 - Determine of MOIDocument70 pages1.2 - Determine of MOIaniketkumarverma475No ratings yet
- Chapter NineDocument15 pagesChapter Niness1322No ratings yet
- Poisson's Equation in ElectrostaticsDocument7 pagesPoisson's Equation in ElectrostaticsSameh HegazyNo ratings yet
- 1 Mechanics: ContentDocument9 pages1 Mechanics: ContentJoe RowingNo ratings yet
- Lecture Sheet 5 - Centroid & Moment of InertiaDocument49 pagesLecture Sheet 5 - Centroid & Moment of InertiaNafin Afnan100% (1)
- Procedure 1: take highest and lowest values of cosθ (1 and -1) =>Document2 pagesProcedure 1: take highest and lowest values of cosθ (1 and -1) =>bltbackwardsNo ratings yet
- Opt Prob 10zDocument5 pagesOpt Prob 10zalejandro_ledesma_15No ratings yet
- Bending Stress in Beams: FormulaDocument11 pagesBending Stress in Beams: Formulawatersoul.nNo ratings yet
- QFT BoccioDocument63 pagesQFT Bocciounima3610No ratings yet
- Derivation For The Moment of Inertia of A Hollow CylinderDocument6 pagesDerivation For The Moment of Inertia of A Hollow CylinderJason HaNo ratings yet
- Lecture 8 Properties of Plane Surfaces I First Moment and Centroid of AreaDocument19 pagesLecture 8 Properties of Plane Surfaces I First Moment and Centroid of AreaAnonymous yorzHjDBdNo ratings yet
- QM PostulatesDocument11 pagesQM PostulatesMobashar AhmadNo ratings yet
- Particle Notes: Ryan D. Reece July 9, 2007Document12 pagesParticle Notes: Ryan D. Reece July 9, 2007jamaeeNo ratings yet
- SSA 3 TrebuchetDocument9 pagesSSA 3 TrebuchetemomNo ratings yet
- Centroids and Centre of GravityDocument31 pagesCentroids and Centre of Gravitysakshm guptaNo ratings yet
- APPLICATION 6 Moment of InertiaDocument44 pagesAPPLICATION 6 Moment of InertiaAnais RosalNo ratings yet
- MIT8 962S20 Pset06Document5 pagesMIT8 962S20 Pset06Robin Red MsiskaNo ratings yet
- Unit 16 Further Applications of Integralcalculus: StructureDocument31 pagesUnit 16 Further Applications of Integralcalculus: StructuretimirkantaNo ratings yet
- 2010 08 14 NotesOnFluidMechanicsAndGasDynamics Wassgren PDFDocument723 pages2010 08 14 NotesOnFluidMechanicsAndGasDynamics Wassgren PDFRaji0% (1)
- Distributed Forces Centroids and C of GravityDocument55 pagesDistributed Forces Centroids and C of GravityTuhafeni HailekaNo ratings yet
- Oscillatory Motion - UWDocument11 pagesOscillatory Motion - UWmostafabahaa258No ratings yet
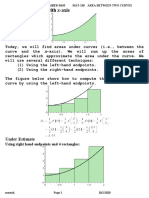
- MAT130.5 (MTM) Handout #8 - Area Between Two Curves, Spring 2020Document25 pagesMAT130.5 (MTM) Handout #8 - Area Between Two Curves, Spring 2020Tasnim Alam Piyash 1731712No ratings yet
- Motion Along A Straight Line.: AP Physics C Review Equations For MechanicsDocument4 pagesMotion Along A Straight Line.: AP Physics C Review Equations For MechanicsCyou97No ratings yet
- Moment of Inertia: I.E. P X (X) PXDocument6 pagesMoment of Inertia: I.E. P X (X) PXafzal taiNo ratings yet
- Rodrigues & Vaz - Subluminal and Superluminal Slution in Vacuum of Maxwell Equations and Massless Dirac Equation 1995Document8 pagesRodrigues & Vaz - Subluminal and Superluminal Slution in Vacuum of Maxwell Equations and Massless Dirac Equation 1995theherbsmithNo ratings yet
- The Complete Spectrum of The Area From Recoupling Theory in Loop Quantum GravityDocument12 pagesThe Complete Spectrum of The Area From Recoupling Theory in Loop Quantum GravityPatrick WongNo ratings yet
- What Is A Wave? Forward vs. Backward Propagating Waves The One-Dimensional Wave EquationDocument22 pagesWhat Is A Wave? Forward vs. Backward Propagating Waves The One-Dimensional Wave EquationEster DanielNo ratings yet
- C - fakepathII Applied Physics MaterialDocument158 pagesC - fakepathII Applied Physics Materialkhalilof.090No ratings yet
- Static Equilibrium: M M M F F FDocument41 pagesStatic Equilibrium: M M M F F FINMENo ratings yet
- Oscillations2007 PDFDocument11 pagesOscillations2007 PDFaldo costradaNo ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Problems in Quantum Mechanics: Third EditionFrom EverandProblems in Quantum Mechanics: Third EditionRating: 3 out of 5 stars3/5 (2)
- Neeraj Kumar Chaudhary: PhysicsDocument180 pagesNeeraj Kumar Chaudhary: PhysicsAshutosh Anand AshuNo ratings yet
- Applications in Ch4Document7 pagesApplications in Ch4(FU HCM) Trần Thanh HiệpNo ratings yet
- Quadrature of The Circle - Edward GoodwinDocument4 pagesQuadrature of The Circle - Edward GoodwinzahkulNo ratings yet
- NML Book ListDocument2 pagesNML Book ListsdfasfsssNo ratings yet
- GDT NotesDocument307 pagesGDT NotesSachsNo ratings yet
- Paper Folding: Fun For Kids!Document34 pagesPaper Folding: Fun For Kids!Mihaela Teodora100% (3)
- EMFTDocument59 pagesEMFTAnshul BhutaniNo ratings yet
- Homogeneous Transformation Matrices Example: Puma 560: ©2017 Max DonathDocument19 pagesHomogeneous Transformation Matrices Example: Puma 560: ©2017 Max DonathchrisNo ratings yet
- 10-3 Arcs and ChordsDocument6 pages10-3 Arcs and Chordsabc123asdNo ratings yet
- 788272-Class - 5-Symmetry, Patterns and Nets WorksheetDocument4 pages788272-Class - 5-Symmetry, Patterns and Nets WorksheetCBD BDNo ratings yet
- MCQ SurveyingDocument7 pagesMCQ Surveyingsarveshfdk48100% (1)
- # SolutionDocument12 pages# SolutionGiraffe thingNo ratings yet
- M A T H E M A T I C S: Bansal ClassesDocument2 pagesM A T H E M A T I C S: Bansal ClassesRahul Kumar SharmaNo ratings yet
- Sheet 1Document9 pagesSheet 1Tony AtefNo ratings yet
- Syllabus Grade 11Document4 pagesSyllabus Grade 11Mohammed AbdallahNo ratings yet
- Computer Graphics 2D TranslationDocument6 pagesComputer Graphics 2D TranslationSample UseNo ratings yet
- IIT JAM Mathematics Preparation: Books, Syllabus, Exam Pattern!Document11 pagesIIT JAM Mathematics Preparation: Books, Syllabus, Exam Pattern!Kadamb Sachdeva0% (1)
- Basic Mathematical Tools For Imaging and Visualization: Dr. Tobias LasserDocument15 pagesBasic Mathematical Tools For Imaging and Visualization: Dr. Tobias LasserhisuinNo ratings yet
- Maths PaperDocument9 pagesMaths PaperSudhir DixitNo ratings yet
- LAB 11: Implementation of Forward & Inverse Kinematics On 3 DOF Manipulator in MATLABDocument12 pagesLAB 11: Implementation of Forward & Inverse Kinematics On 3 DOF Manipulator in MATLABGHULAM ESSANo ratings yet
- Aircraft Symmetric LoadsDocument13 pagesAircraft Symmetric LoadsNavish KotwalNo ratings yet
- Assignment 2: Robotics SystemsDocument8 pagesAssignment 2: Robotics SystemsJoshua FindlayNo ratings yet
- Elliptical Lobe Shape Gerotor Pump Design To Minimize Wear: Research ArticleDocument6 pagesElliptical Lobe Shape Gerotor Pump Design To Minimize Wear: Research ArticleLucas DuarteNo ratings yet
- LLL WikipediaDocument7 pagesLLL Wikipedia00carambolaNo ratings yet
- Time and CircumferenceDocument7 pagesTime and CircumferenceVine AlparitoNo ratings yet
- Applications of Analytic GeometryDocument15 pagesApplications of Analytic GeometrydaniloNo ratings yet
- 30-C-2 - Maths (Standard)Document23 pages30-C-2 - Maths (Standard)Sagar TiwariNo ratings yet
Mi 1
Mi 1
Uploaded by
mekoaaaOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Mi 1
Mi 1
Uploaded by
mekoaaaCopyright:
Available Formats
MOMENT OF INERTIA
Moments of Area
Example 1: Pressure on a dam
The left figure shows a dam bounding a body of water. Acting at
any point is a water pressure which is a force per unit of area
Water pressure is a function of both water specific weight ( ) and
water depth (x). The pressure is constant across an area of
infinitely small height dx and width 'L' but will vary linearly with
height 'x' as p x =x
First Moment of Area
Assume pressure p(x) is applied to
elemental area dA.
Element dA is located a distance 'x' below
the z-axis.
If we multiply this elemental area by distance
'x', we can define elemental moment:
dM = xdA
or if expressed algebraically
M i = xAi
Integrating, we find the statical or first
moment of area as: M = A xdA
expressed algebraically as
M = xA i
i
Second Moment of Area
If we take an element of area dA and
multiply it by pressure p(x)...
...the elemental force acting on dA is:
dF = p xdA
If we multiply this elemental moment by its
distance 'x' from the z-axis, we have:
dF = p xdA
The moment of dF about the z-axis is:
dM = xdF
2
dM = x xdA = x dA
Second Moment of Area
If we define as a constant and divide it out, we are left with:
dM = x xdA
Mathematically, this is a moment of the first moment of area,
thus we refer to this as the second moment of area.
The moment of the entire distribution is equal to the integral
of dM over the entire area.
2
M = A dM = A x dA
Algebraically, we can replace elemental area dA with some
area Ai of finite size. Total moment is then the sum of all
individual moments.
M = x 2Ai
i
Second Moment of Area
Thus, the second moment of area...
...is often called area moment of inertia due to the
similarity to the mathematical form of the integral for the
resultant moments of the inertia forces in the case of
rotating bodies (i.e.: mass moment of inertia).
For our purposes, we will hereafter refer to the second
moment of area simply as the moment of inertia
As such, the moment of interia is defined as:
2
I = A distance dA
An algebraic approximation can be expressed as:
I = distance 2 Ai
i
Area Moment of Inertia
Example 2:
Beam Bending - Stress
A common application is to
determine the internal bending
stress in a beam. Such stresses
are linear.
Analysis of these stresses is a
strength of materials topic and
does require the moment of
inertia of the beam cross section.
This will be addressed in detail in
your strength of materials course
b =
7
My
I
Area Moment of Inertia
Example 3:
Beam Bending Deflection
Consider bending the same
beam in two planes...for
example, a 2 x 4 laid across a
pair of carpenter's horses.
Now try with your own ruler.
About which axis is the ruler
'stiffer'?
Study the equation for moment of inertia again.
2
I = A distance dA
Notice that for a given cross section, it is not area that matters,
it is the orientation of the section.
8
Area Moment of Inertia
As stated previously, the second moment of area, or area
moment of inertia, is given by:
I = A distance 2 dA
Let's consider finding the moment of inertia about some
arbitrary 'x' or 'y' axis. Consider cross section below with area
'A'. Elemental area dA is located a
Y
x
distance 'x' from the y-axis and a
distance 'y' from the x-axis. Then:
I x = A y 2 dA
I y = A x 2 dA
dA
y
X
The units of moment of inertia will be length to the fourth power
such as in4, ft4, mm4, or m4
9
Centroidal Moment of Inertia
In most cases, we are interested in the moment of inertia
about an x-y axis superimposed on the centroid of the cross
section. This is known as the centroidal moment of inertia.
Centroidal moments of inertia for simple geometric shapes
can be found in many engineering handbooks, on the Internet,
and in the appendix of this online text.
But before we use such handbook data, let's apply the
general equation for moment of inertia to a rectangular cross
section.
10
Centroidal Moment of Inertia
Consider a rectangle with a base width 'b' and a height 'h'.
The application of calculus will yield:
y
dA = bdy
dy
I xc = y dA =
A
y bdy
h / 2
[ ]
3
h /2
2
h/ 2
y
b h
h
= b =
3 h/ 2 3 2
2
bh
12
y
x dx
b/ 2
I yc = x dA =
2
b/ 2
3
[ ]
3
b /2
x
h b
b
= h =
3 b / 2 3 2
2
11
x hdx
3
hb
12
dA = hdx
Centroidal Moment of Inertia
We can also estimate the moment of inertia using algebraic
methods. By breaking the area into finite sections (lets try
four), then the moment of inertia (Ixc only) calculates as:
y
Ai = b
h/ 4
3h
8
h
3h
8
h/ 4
h
8
h
8
h/ 4
h/ 4
h
4
I xc = y A i
[ ] [ ] [ ] [ ]
[ ]
2
3h
h
h
h
h
h
3h
h
=
b
b
b
b
8
4
8
4
8
4
8
4
2
3h
=
8
5bh
=
64
3h
h
b
4
Note this does not equal the moment of inertia calculated using
calculus methods. We can get closer by breaking the area into
more and smaller rectangles.
12
Centroidal Moment of Inertia
For example, by dividing the rectangle into 8 equal areas, we
would calculate the moment of inertia to be:
I xc = y 2Ai
[ ]
7h
=
16
5h
16
3h
16
168 h
h
=
b =
256
8
21bh
256
16
16
3h
16
5h
16
7h
16
h
b
8
Although much closer to the result obtained through
integration, it is still not equal. Although we could continue
to divide this rectangle into even smaller areas to refine the
solution, it is unneccessary. Integrations have been
accomplished for common geometric shapes and are
tabulated in the appendix to this online text.
13
Centroidal Moment of Inertia
When applying the relationships listed in the appendix, take
care to note the location of the x-y coordinate axis. Moments
of inertia can be found about any axis one wishes.
For example, the moment of inertia of a rectangle about an
x-axis depends on the x-axis in which you are interested, the
centroidal axis or the base axis.
y'
x'
c
b
14
bh 3
I x' =
12
bh3
Ix=
3
b 3h
I y' =
12
3
b h
Iy =
3
You might also like
- Solution Manual For Modern Quantum Mechanics 2nd Edition by SakuraiDocument13 pagesSolution Manual For Modern Quantum Mechanics 2nd Edition by SakuraiRyo Kinase36% (14)
- Assignment 2F: ProjectionDocument2 pagesAssignment 2F: ProjectionGábor KölesNo ratings yet
- WORKSHEET-understanding Quadrilaterals - Class 8Document12 pagesWORKSHEET-understanding Quadrilaterals - Class 8Manoj Pandey60% (5)
- Townsend, Quantum Physics, CHAP - 3, Schodinger EqDocument24 pagesTownsend, Quantum Physics, CHAP - 3, Schodinger EqElcan DiogenesNo ratings yet
- Engineering MechanicDocument24 pagesEngineering MechanicManoj BallaNo ratings yet
- Chapter 6 - Moments of InertiaDocument20 pagesChapter 6 - Moments of InertiaLetshego Itumeleng MoahloliNo ratings yet
- Applications of Double and Triple IntegralsDocument7 pagesApplications of Double and Triple IntegralsRyan YeeNo ratings yet
- Bending Stress in Beams: Basic AssumptionsDocument9 pagesBending Stress in Beams: Basic AssumptionspidotnasirNo ratings yet
- Chapter 3.a (CG Centroid)Document21 pagesChapter 3.a (CG Centroid)LogarithemNo ratings yet
- Aplicaciones de La Integral DobleDocument91 pagesAplicaciones de La Integral DobleCristian Andres Fuentes CarbajalNo ratings yet
- MP13 Quantum Mechanics 2Document40 pagesMP13 Quantum Mechanics 2Ahmad Fikry IskandarNo ratings yet
- Jackson 8.1 Homework Problem SolutionDocument4 pagesJackson 8.1 Homework Problem SolutionDaniel GuerreroNo ratings yet
- MEG 214 - 8aDocument49 pagesMEG 214 - 8aSimiloluwa ObasaNo ratings yet
- CurveDocument19 pagesCurveSheryll de GuzmanNo ratings yet
- Lecture #19: Moments of InertiaDocument19 pagesLecture #19: Moments of InertiaAfiqah ZainuddinNo ratings yet
- Centroids and Centre of GravityDocument56 pagesCentroids and Centre of GravitydearsaswatNo ratings yet
- Chapter 6 Moment of InertiaDocument30 pagesChapter 6 Moment of Inertiaomar tahaNo ratings yet
- Nuclear PhysicsDocument11 pagesNuclear Physicsgiovanny_francisNo ratings yet
- Bending Stress of BeamsDocument18 pagesBending Stress of BeamsRambabu RNo ratings yet
- Moment of InertiaDocument15 pagesMoment of InertiamotahareshNo ratings yet
- KIX1001 - Week 9 (2023-2024)Document47 pagesKIX1001 - Week 9 (2023-2024)haqeemifarhanNo ratings yet
- University Institute of Engineering Academic Unit 3Document38 pagesUniversity Institute of Engineering Academic Unit 3Vinoth Rouge RockersNo ratings yet
- Applications of Differential EquationsDocument28 pagesApplications of Differential Equationsmaths203No ratings yet
- Quantum Field Theory Notes: Ryan D. Reece November 27, 2007Document23 pagesQuantum Field Theory Notes: Ryan D. Reece November 27, 2007jamaeeNo ratings yet
- Concentrated Forces:: Unit IV Distributed ForcesDocument11 pagesConcentrated Forces:: Unit IV Distributed Forcesbpal1970No ratings yet
- Basic Concepts:: U (1/2EI) M (X) DX U L: V And, Since W UDocument7 pagesBasic Concepts:: U (1/2EI) M (X) DX U L: V And, Since W UAberaMamoJaletaNo ratings yet
- 1.2 - Determine of MOIDocument70 pages1.2 - Determine of MOIaniketkumarverma475No ratings yet
- Chapter NineDocument15 pagesChapter Niness1322No ratings yet
- Poisson's Equation in ElectrostaticsDocument7 pagesPoisson's Equation in ElectrostaticsSameh HegazyNo ratings yet
- 1 Mechanics: ContentDocument9 pages1 Mechanics: ContentJoe RowingNo ratings yet
- Lecture Sheet 5 - Centroid & Moment of InertiaDocument49 pagesLecture Sheet 5 - Centroid & Moment of InertiaNafin Afnan100% (1)
- Procedure 1: take highest and lowest values of cosθ (1 and -1) =>Document2 pagesProcedure 1: take highest and lowest values of cosθ (1 and -1) =>bltbackwardsNo ratings yet
- Opt Prob 10zDocument5 pagesOpt Prob 10zalejandro_ledesma_15No ratings yet
- Bending Stress in Beams: FormulaDocument11 pagesBending Stress in Beams: Formulawatersoul.nNo ratings yet
- QFT BoccioDocument63 pagesQFT Bocciounima3610No ratings yet
- Derivation For The Moment of Inertia of A Hollow CylinderDocument6 pagesDerivation For The Moment of Inertia of A Hollow CylinderJason HaNo ratings yet
- Lecture 8 Properties of Plane Surfaces I First Moment and Centroid of AreaDocument19 pagesLecture 8 Properties of Plane Surfaces I First Moment and Centroid of AreaAnonymous yorzHjDBdNo ratings yet
- QM PostulatesDocument11 pagesQM PostulatesMobashar AhmadNo ratings yet
- Particle Notes: Ryan D. Reece July 9, 2007Document12 pagesParticle Notes: Ryan D. Reece July 9, 2007jamaeeNo ratings yet
- SSA 3 TrebuchetDocument9 pagesSSA 3 TrebuchetemomNo ratings yet
- Centroids and Centre of GravityDocument31 pagesCentroids and Centre of Gravitysakshm guptaNo ratings yet
- APPLICATION 6 Moment of InertiaDocument44 pagesAPPLICATION 6 Moment of InertiaAnais RosalNo ratings yet
- MIT8 962S20 Pset06Document5 pagesMIT8 962S20 Pset06Robin Red MsiskaNo ratings yet
- Unit 16 Further Applications of Integralcalculus: StructureDocument31 pagesUnit 16 Further Applications of Integralcalculus: StructuretimirkantaNo ratings yet
- 2010 08 14 NotesOnFluidMechanicsAndGasDynamics Wassgren PDFDocument723 pages2010 08 14 NotesOnFluidMechanicsAndGasDynamics Wassgren PDFRaji0% (1)
- Distributed Forces Centroids and C of GravityDocument55 pagesDistributed Forces Centroids and C of GravityTuhafeni HailekaNo ratings yet
- Oscillatory Motion - UWDocument11 pagesOscillatory Motion - UWmostafabahaa258No ratings yet
- MAT130.5 (MTM) Handout #8 - Area Between Two Curves, Spring 2020Document25 pagesMAT130.5 (MTM) Handout #8 - Area Between Two Curves, Spring 2020Tasnim Alam Piyash 1731712No ratings yet
- Motion Along A Straight Line.: AP Physics C Review Equations For MechanicsDocument4 pagesMotion Along A Straight Line.: AP Physics C Review Equations For MechanicsCyou97No ratings yet
- Moment of Inertia: I.E. P X (X) PXDocument6 pagesMoment of Inertia: I.E. P X (X) PXafzal taiNo ratings yet
- Rodrigues & Vaz - Subluminal and Superluminal Slution in Vacuum of Maxwell Equations and Massless Dirac Equation 1995Document8 pagesRodrigues & Vaz - Subluminal and Superluminal Slution in Vacuum of Maxwell Equations and Massless Dirac Equation 1995theherbsmithNo ratings yet
- The Complete Spectrum of The Area From Recoupling Theory in Loop Quantum GravityDocument12 pagesThe Complete Spectrum of The Area From Recoupling Theory in Loop Quantum GravityPatrick WongNo ratings yet
- What Is A Wave? Forward vs. Backward Propagating Waves The One-Dimensional Wave EquationDocument22 pagesWhat Is A Wave? Forward vs. Backward Propagating Waves The One-Dimensional Wave EquationEster DanielNo ratings yet
- C - fakepathII Applied Physics MaterialDocument158 pagesC - fakepathII Applied Physics Materialkhalilof.090No ratings yet
- Static Equilibrium: M M M F F FDocument41 pagesStatic Equilibrium: M M M F F FINMENo ratings yet
- Oscillations2007 PDFDocument11 pagesOscillations2007 PDFaldo costradaNo ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Problems in Quantum Mechanics: Third EditionFrom EverandProblems in Quantum Mechanics: Third EditionRating: 3 out of 5 stars3/5 (2)
- Neeraj Kumar Chaudhary: PhysicsDocument180 pagesNeeraj Kumar Chaudhary: PhysicsAshutosh Anand AshuNo ratings yet
- Applications in Ch4Document7 pagesApplications in Ch4(FU HCM) Trần Thanh HiệpNo ratings yet
- Quadrature of The Circle - Edward GoodwinDocument4 pagesQuadrature of The Circle - Edward GoodwinzahkulNo ratings yet
- NML Book ListDocument2 pagesNML Book ListsdfasfsssNo ratings yet
- GDT NotesDocument307 pagesGDT NotesSachsNo ratings yet
- Paper Folding: Fun For Kids!Document34 pagesPaper Folding: Fun For Kids!Mihaela Teodora100% (3)
- EMFTDocument59 pagesEMFTAnshul BhutaniNo ratings yet
- Homogeneous Transformation Matrices Example: Puma 560: ©2017 Max DonathDocument19 pagesHomogeneous Transformation Matrices Example: Puma 560: ©2017 Max DonathchrisNo ratings yet
- 10-3 Arcs and ChordsDocument6 pages10-3 Arcs and Chordsabc123asdNo ratings yet
- 788272-Class - 5-Symmetry, Patterns and Nets WorksheetDocument4 pages788272-Class - 5-Symmetry, Patterns and Nets WorksheetCBD BDNo ratings yet
- MCQ SurveyingDocument7 pagesMCQ Surveyingsarveshfdk48100% (1)
- # SolutionDocument12 pages# SolutionGiraffe thingNo ratings yet
- M A T H E M A T I C S: Bansal ClassesDocument2 pagesM A T H E M A T I C S: Bansal ClassesRahul Kumar SharmaNo ratings yet
- Sheet 1Document9 pagesSheet 1Tony AtefNo ratings yet
- Syllabus Grade 11Document4 pagesSyllabus Grade 11Mohammed AbdallahNo ratings yet
- Computer Graphics 2D TranslationDocument6 pagesComputer Graphics 2D TranslationSample UseNo ratings yet
- IIT JAM Mathematics Preparation: Books, Syllabus, Exam Pattern!Document11 pagesIIT JAM Mathematics Preparation: Books, Syllabus, Exam Pattern!Kadamb Sachdeva0% (1)
- Basic Mathematical Tools For Imaging and Visualization: Dr. Tobias LasserDocument15 pagesBasic Mathematical Tools For Imaging and Visualization: Dr. Tobias LasserhisuinNo ratings yet
- Maths PaperDocument9 pagesMaths PaperSudhir DixitNo ratings yet
- LAB 11: Implementation of Forward & Inverse Kinematics On 3 DOF Manipulator in MATLABDocument12 pagesLAB 11: Implementation of Forward & Inverse Kinematics On 3 DOF Manipulator in MATLABGHULAM ESSANo ratings yet
- Aircraft Symmetric LoadsDocument13 pagesAircraft Symmetric LoadsNavish KotwalNo ratings yet
- Assignment 2: Robotics SystemsDocument8 pagesAssignment 2: Robotics SystemsJoshua FindlayNo ratings yet
- Elliptical Lobe Shape Gerotor Pump Design To Minimize Wear: Research ArticleDocument6 pagesElliptical Lobe Shape Gerotor Pump Design To Minimize Wear: Research ArticleLucas DuarteNo ratings yet
- LLL WikipediaDocument7 pagesLLL Wikipedia00carambolaNo ratings yet
- Time and CircumferenceDocument7 pagesTime and CircumferenceVine AlparitoNo ratings yet
- Applications of Analytic GeometryDocument15 pagesApplications of Analytic GeometrydaniloNo ratings yet
- 30-C-2 - Maths (Standard)Document23 pages30-C-2 - Maths (Standard)Sagar TiwariNo ratings yet