Scribd
Upload
140 views4 pages

Fourier Series & Convolution Tutorial

This document provides tutorial problems for a signals and systems course. It includes problems on Fourier series analysis of periodic signals, including determining Fourier series coefficients and plotting magnitude and phase spectra. It also includes problems on orthogonal signals, continuous-time linear time-invariant systems, and convolution of input signals with system impulse responses.

Uploaded by

Shamim Ali
Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
140 views4 pages

Fourier Series & Convolution Tutorial

This document provides tutorial problems for a signals and systems course. It includes problems on Fourier series analysis of periodic signals, including determining Fourier series coefficients and plotting magnitude and phase spectra. It also includes problems on orthogonal signals, continuous-time linear time-invariant systems, and convolution of input signals with system impulse responses.

Uploaded by

Shamim Ali
Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd

ECE 219: Signal, System & Control

Tutorial Sheet 3 Fourier series & Convolution


Submission date: March. 10, 2015
1) (Fourier series by inspection). Consider the continuous-time periodic signal
(a) Determine the fundamental frequency

and the Fourier series coefficients

(b) Neatly plot the magnitude and the phase spectrum of

such that

2) (Amplitude-phase form of Fourier series). A continuous-time periodic signal


has a fundamental period
. The non-zero Fourier series coefficients for

is real-valued and
are specified as:

Express x(t) in the amplitude-phase form:


3)

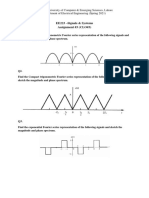
(Properties of Fourier Series Coefficients). Figure 1 shows the magnitude and phase spectra of three
continuous-time periodic signals. Answer the following questions:
(a) For each signal, determine whether the signal is real or complex. Explain your answer.
(b) Which signal is a real-valued and even function? Which signal is a real-valued and odd function?
Explain your answer.
(c) For the signal corresponding to the spectra in Figure 1 (i), do the following:
write a Fourier series equation for the time waveform
.
Find the dc component and average power of this signal.
Find the average power of this signal.

4) (Fourier series of the sawtooth waveform). Consider the continuous-time periodic waveform in Figure
2.
(a) What are the fundamental period and fundamental frequency
of
?
(b) Compute the trigonometric Fourier series coefficients
and
for the signal
. Hint:
,

(c) Neatly plot the magnitude and phase spectrum of


for
.
(d) Consider the following approximation for

up to the fifth harmonic components (i.e.,

Use MATLAB to plot


for
(e) Use MATLAB to find the smallest values of
in the above approximation such that
captures 95% and 99% power in
, respectively .

Figure 1: Figure for Question 3.

Figure 2: Plot of

for question 4.

5) (Fourier series of a continuous-time signal). Consider the following continuous-time signal:

Figure 3: Figure for Question 5.


(a) What are the fundamental period and fundamental frequency
of
(b) Compute the trigonometric Fourier series coefficients for the signal
6) Orthogional signals. The energises of two energy signals
a.

and

?
.

are

If
and
are orthogonal, then show that the energy of the signal
to the energy of the signal
and is given by
.

b. If

and

are orthogonal, find the energies of the signals

and

, respectively.
is identical

and

.
c. We define

If

, the correlation of the two energy signals

and

, as

, then show that

7) Consider a continuous-time LTI system with impulse response h(t) and an input signal x(t) as
shown below. Find and neatly sketch the output y(t).

8) Consider a continuous-time LTI system with impulse response


as shown below. Find and neatly sketch the output
.

***

and input

You might also like