X y y X

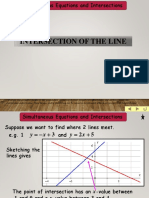
9 Simultaneous Equations, One Linear and One Quadratic
9 Simultaneous Equations,
One Linear and One
Quadratic
4.
(2) (1) 2:
Review Exercise 9 (p. 9.4)
1.
3x 2 y 16 (1)
6 x 7 y 10 (2)
6 x 7 y 2(3 x 2 y ) 10 2( 16)
11 y 22
y2
x 5 2 y (1)
2 x y 1 (2)
By substituting y = 2 into (1), we have
3 x 2( 2) 16
3 x 12
x 4
By substituting (1) into (2), we have

2(5 2 y ) y 1
10 4 y y 1
3 y 9
The solution is x = 4, y = 2.
y 3
x 5 2(3)
1
2.
3x 4 y 6 (1)
y 4 x 8 (2)
3 x 4( 4 x 8) 6
3 x 16 x 32 6
19 x 38
x2
x
y
By substituting x = 2 into (2), we have
3.
y 4( 2) 8
0
3x 4 y 2 (1)
x 3 y 8 (2)
(2) 3 (1):
3( x 3 y ) (3 x 4 y ) 24 2
13 y 26
y 2
x 3( 2) 8
x 2
47
0
0
1
2
2
4
NSS Mathematics in Action 4B Full Solutions
5.
3x 2 y 30 0 ......(1)
5 x 4 y 16 0 ......(2)
(1) 2 + (2):
2(3 x 2 y 30) (5 x 4 y 16) 0

11x 44 0
x4
3( 4) 2 y 30 0
2 y 18 0
y 9
6.
Lets Discuss
Lets Discuss (p. 9.6)

The original method or Angels method are both fine. Kens
method is more tedious as it involves squaring of the expression
(y 1).
6 x 7 y 4 0 ......(1)
2 x 3 y 12 0 ......(2)
Classwork
(1) (2) 3:
Classwork (p. 9.17)
(6 x 7 y 4) 3( 2 x 3 y 12) 0
16 y 32 0
y2
1.
6 x 7(2) 4 0
6 x 18 0
7.
y 2 x 2 x 1 ......(1)
......(2)
y 1 5x
x 3
The two straight lines intersect at (5, 1).

1 5x 2x2 x 1
2x2 6x 0
x 2 3x 0
y = 2x
......(3)
x( x 3) 0
x0
x + 2y = 5
x 0 2 4
y
5 3 1
2 2 2
2.
or
x 3
(3) has two distinct real roots.

The simultaneous equations have 2 distinct real
solutions.
y x 2 3x 2 ......(1)
......(2)
y x6
x 6 x 2 3x 2
x2 4x 4 0
......(3)
( x 2) 0
2
8.
x2
The two straight lines intersect at (1, 2).

(3) has one double real root.

The simultaneous equations have 1 real solution.
2x 3y = 7
x
y
1 2 5
3 1 1
x
y
0
6
x+y=6
48
3
3
6
0
3.
y x 2 2 x 4 ......(1)
......(2)
y 2x 1

Quick Practice
2x 1 x2 2x 4
x2 4x 5 0
......(3)
Quick Practice 9.1 (p. 9.5)
Consider the discriminant of x2 4x + 5 = 0.
y x 1
( 4) 2 4(1)(5)
......(1)
16 20
0
2
y x 7 x 6 ......(2)
(3) has no real roots.

The simultaneous equations have no real solutions.

x 1 x2 7 x 6
x2 8x 7 0
( x 1)( x 7) 0
x 1 or x 7
y=11=0
y=71=6
The solutions of the simultaneous equations are (1, 0) and
(7, 6).
y 3x 2 4 x 2
......(1)
3x y 4 0
......(2)
From (2), we have

y = 3x 4 (3)
3x 4 3x 2 4 x 2
3x 2 7 x 2 0
( x 2)(3 x 1) 0
x 2 or x
1
3

y = 3(2) 4 = 2
By substituting x =
y = 3
1
into (3), we have
3
1
4 3
3
The solutions of the simultaneous equations are (2, 2) and
, 3 .
3
x 2 2 y 2 3 ......(1)
x 2 y 1
......(2)
From (2), we have

x = 2y 1 (3)
49

x = 2(1) 1 = 1
(2 y 1) 2 2 y 2 3
4 y 4 y 1 2 y 3
2
By substituting y
6y 4y 2 0
2
5
1
x 2 1
3
3
3y 2 2 y 1 0
( y 1)(3 y 1) 0
y 1 or y
1
into (3), we have
3
The solutions of the simultaneous equations are
1
3
5 1
,
3 3
and (1, 1).

The perimeter of the rectangle is 82 cm.
2x + 2y = 82
x y 41
i.e. CD AD
2
AC
x y 29
2
......(1)
(Pyth. theorem)
x 2 y 2 841
......(2)
The above gives us a pair of simultaneous equations.
x y 41
......(1)
2
2
x
y
841 ......(2)
From (1), we have

y = 41 x (3)
x 2 (41 x) 2 841
x 2 1681 82 x x 2 841
2 x 2 82 x 840 0
x 2 41x 420 0
( x 20)( x 21) 0
x 20 or x 21
y = 41 (20) = 21
y = 41 (21) = 20
x20 x21
or
y 21 y 20

Let x be the tens digit and y be the units digit of the original
integer.
The original integer is 10x + y, and the reversed integer is
10y + x.
(10 y x) (10 x y ) 45
9 x 9 y 45
x y 5
y x5
......(1)
The sum of the squares of the two digits is 73.

x2 + y2 = 73
(2)
50

x ( x 5) 73
2
x x 10 x 25 73
2
2 x 2 10 x 48 0
x 2 5 x 24 0
( x 8)( x 3) 0
x 8 or x 3 (rejected)
3 x
2
x
y
1 1
2 1
3
0

y = (8) 5 = 3
The integer is 83.
The two graphs intersect at (0.5, 1.8) and (3, 0).

The solutions of the simultaneous equations are (0.5, 1.8)
and (3, 0).
y = 2x + 1
x
y
0
1
1 2
1 3
The two graphs intersect at only one point (0, 1).

The solution of the simultaneous equations is (0, 1).
y = x + 2
x
y
0
2
2
0
4
2
The two graphs do not intersect.

51

y 2
2
y 2 x 3x k ......(1)
......(2)
4 x y 2
2
(a)
4 x 2 2 x 2 3x k
2 x x ( k 2) 0
(b)
......(4)
( 1) 4( 2)( k 2) 0
2
17 8k 0
k
17
8
17
into (4), we have
8
(b) By substituting k
17
2 0
8
1
2x 2 x 0
8
2
16 x 8 x 1 0
2x 2 x
( 4 x 1) 2 0
1
x
4
1
By substituting x
into (3), we have
4
1
y 4 2 3
4
The solution of the simultaneous equations is
1
, 3 .
4
Further Practice
Further Practice (p. 9.9)
1.
(a)
2 x 2 y 0 ......(1)
y 13x 6 0 ......(2)
From (1), we have
y = 2x2
(3)
2 x 2 13x 6 0
(2 x 1)( x 6) 0
x
1
or x 6
2
By substituting x
1
2
1 1
, and (6, 72).
2 2
2 x 2 y 1 0 ......(1)
2
y 2 x 7 x 5 ......(2)
The simultaneous equations have only one real

solution.

y = 2(6)2 = 72
From (2), we have

y = 4x + 2
(3)
2
1
into (3), we have
2
52
( 40 2 y ) y 200
y ( 20 y ) 100
2 x 2(2 x 2 7 x 5) 1 0
4 x 2 12 x 9 0
y 2 20 y 100 0
( 2 x 3) 2 0
x
By substituting x
( y 10) 2 0
y 10
3
2
x 40 2(10)
20
3
into (1), we have
2
3
2
2y 1 0
2
2y 2 0
y 1
, 1 .
(c)
st 2
......(1)
2
2
2s t 1 ......(2)
From (1), we have
t = 2 s (3)
2s 2 (2 s) 2 1
2s 2 4 4 s s 2 1
3s 2 4 s 3 0
Consider the discriminant of 3s 2 4 s 3 0 .
( 4) 2 4(3)(3)
20
0
2.
The simultaneous equations have no real

solutions.
(a) Perimeter of the smaller rectangle
2
2 y cm
2
( x 2 y ) cm
x + 2y = 40
Area of the rectangle ABCD = xy cm2
xy = 200
The simultaneous equations are
x 2 y 40
xy 200
(b)
x 2 y 40 ......(1)
xy 200 ......(2)
From (1), we have
x 40 2 y
(3)
53
The dimensions of rectangle are 10 cm 20 cm.
Exercise
Further Practice (p. 9.15)

(a) y = 3x 5
x
y
1 2
2 1
3
4
Exercise 9A (p. 9.10)

Level 1
y 2 x 4 (1)
1.
2
y x 1 (2)
2x 4 x2 1
x2 2x 3 0
( x 1)( x 3) 0

x 1 or x 3
By substituting x = 1 into (1), we have y = 2(1) + 4 = 2
(1, 2) and (3, 10).
(b) y = 2x 2
x 2 1 0
y 2 0 2
y x 2 2 x 13 (1)
y 4 x 12 (2)
2.
4 x 12 x 2 2 x 13
x2 2x 1 0
(c) x + y = 2
x
y
1 0
1 2
( x 1) 2 0
x 1

(1, 16).
1
3
x 9 y 6 0 (1)
3.
2
x 3y
(2)

3y 2 9 y 6 0
y 2 3y 2 0
( y 1)( y 2) 0
The two graphs intersect at (1, 1) and (3, 5).

The solutions of the simultaneous equations are (1,
1) and (3, 5).
y 1 or y 2
By substituting y = 1 into (2), we have x = 3(1)2 = 3
By substituting y = 2 into (2), we have x = 3(2)2 = 12
(3, 1) and (12, 2).
4.
x y 3
(1)
2
x 4 y 3 y 7 (2)
4 y2 3y 7 y 3
4 y2 4 y 4 0
y2 y 1 0
54

Consider the discriminant of y2 + y + 1 = 0.
12 4(1)(1)
x 3 y 7 0 (1)
5.
3
0
2
2
x y 9 (2)
From (1), we have

x 3 y 7 (3)
(3 y 7)2 y 2 9
9 y 2 42 y 49 y 2 9
8 y 2 42 y 40 0
4 y 2 21y 20 0
(4 y 5)( y 4) 0
y
5
or y 4
4
5
into (3), we have
4
By substituting y
13
5
x 3
7
4
4
By substituting y = 4 into (3), we have x = 3(4) 7 = 5
13 5
, and (5, 4).
4 4
2 x y 7 0 (1)
6.
2
2
x y 1
( 2 )
From (1), we have

y 2 x 7 (3)
x 2 ( 2 x 7) 2 1
x 2 4 x 2 28 x 49 1
5 x 2 28 x 48 0
Consider the discriminant of 5x2 + 28x + 48 = 0.
282 4(5)( 48)

176
7.
x 2 y 5 (1)
2
x
4 xy 3 (2)
From (1), we have
x5
2
(3)
55
x 5
3
2
x 2 4 x
7
1
, and (3, 1).
3
3
x 2 2 x( x 5) 3
x 2 2 x 2 10 x 3
3x 2 10 x 3 0
( x 3)(3 x 1) 0
x y 1 0
(1)
8.
2
2
x xy y 7 (2)
1
x 3 or x
3
From (1), we have

y x 1
(3)
35
1
2
1
By substituting x
into (3), we have
3
1
5
7
3
y
2
3
y
x 2 x( x 1) ( x 1) 2 7
x 2 x 2 x x 2 2x 1 7
x2 x 6 0
( x 2)( x 3) 0
x 2 or x 3
By substituting x 2 into (3), we have
y = 2 1 = 3
y=31=2
3) and (3, 2).
9.
x y = 2xy 5x = 6
x y 6 (1)
2 xy 5x 6 (2)
From (1), we have
y x6
(3)
2 x( x 6) 5 x 6
2 x 12 x 5 x 6 0
2
2x 2 7 x 6 0
( x 2)(2 x 3) 0
x 2 or x
3
2

y = 2 + 6 = 4
3
into (3), we have
2
3
9
y 6
2
2
By substituting x
(2, 4) and
3 9
, .
2 2
10. x2 4y2 = 2x y = 5
x 2 4 y 2 5 (1)
2x y 5
From (3), we have
56
(2)
y 2 x 5 (3)
By substituting x
x 2 4(2 x 5) 2 5
7
into (3), we have
3
1
7
y 2 5
3
3

x 2 4( 4 x 2 20 x 25) 5
x 2 16 x 2 80 x 100 5

y = 2(3) 5 = 1
15 x 2 80 x 105 0
3x 2 16 x 21 0
1
7
, and (3, 1).
3
3
(3 x 7)( x 3) 0
7
x
or x 3
3
11. Let x cm and y cm be the length and the width of the

rectangle respectively.
The perimeter of the rectangle is 46 cm.
2 x 2 y 46
x y 23
y 23 x (1)
The area of the rectangle is 120 cm2.

xy 120 ( 2)
x(23 x) 120
23x x 2 120
x 2 23 x 120 0
( x 8)( x 15) 0
x 8 or x 15
y = 23 8 = 15
y = 23 15 = 8
The dimensions of the rectangle are 8 cm 15 cm.
12. Let x be the tens digit and y be the units digit of the original
integers.
The original integer is 10x + y, and the reversed
integer is 10y + x.
(10 y x) (10 x y ) 18
9 y 9 x 18
yx2
y x 2 (1)
The product of the two integers is 1855.
(10 y x )(10 x y ) 1855
10 y 2 10 x 2 101xy 1855 ( 2)

10( x 2) 2 10 x 2 101x( x 2) 1855
10( x 2 4 x 4) 10 x 2 101( x 2 2 x ) 1855
121x 2 242 x 1815 0
x 2 2 x 15 0
( x 3)( x 5) 0
x 3 or
x 5
(rejected)

y=3+2=5
The original integer is 35.
57

13. Let x cm and y cm be the length and the width of the
y
x
Then the length of the equilateral triangle is also y cm.
The perimeter of the figure is 40 cm.
2 x 4 y 40
x 2 y 20
x 20 2 y (1)
The area of the rectangle is 50 cm2.

xy 50
( 2)
( 20 2 y ) y 50
20 y 2 y 2 50
2 y 2 20 y 50 0
y 2 10 y 25 0
( y 5) 2 0
y5
By substituting y = 5 into (1), we have x = 20 2(5) = 10
The dimensions of the rectangle are 5 cm 10 cm.
Level 2
14.
y 6 4( x 3) (1)
2
y 2 xy 36 (2)
From (1), we have
y6
x3
4
y 6 12
x
4
y6
x
(3)
4
y 6
y 2 2
y 36
4
2 y 2 ( y 6) y 72
3 y 2 6 y 72 0
y 2 2 y 24 0
( y 6)( y 4) 0
y 6 or y 4
66
0
4
4 6
5
4
2
, 4 and (0, 6).

2
58
15.
2 x 3 y 3 (1)
17.
2
xy y 4 (2)
3 3y
y y2 4
2
3y 3y2 2 y2 8
5 y2 3y 8 0
(5 y 8)( y 1) 0
8
or y 1
5
8
By substituting y into (3), we have
5
y
8
3 3
5 9
x
2
10
16.
3 3(1)
3
2
9
8
, and (3, 1).
10
5
y 5 x 2y
(1)
2
3
2 x 2 y 2 15 0 (2)
From (1), we have
3( y 5) 2( x 2 y )
3 y 15 2 x 4 y
y 2 x 15 (3)
2 x 2 ( 2 x 15) 2 15 0
2 x 2 ( 4 x 2 60 x 225) 15 0
6 x 2 60 x 240 0
x 2 10 x 40 0
Consider the discriminant of x2 + 10x + 40 = 0.
10 2 4(1)(40)
60
( 2)
From (1), we have
3 3y
x
(3)
2
2
2
5x y 1
From (1), we have
5x 2 y 1 0 (1)
59
5x 1
2
(3)

5x 1
2 y 2 3 y 2 y 2 y 2 12
2
2
9 2
9 2
y 12 y 8 y 6 y 2 y 2 12 0
2
2
2 y2 6 y 4 0
5x 2
(5 x 1) 2
1
4
20 x 2 ( 25 x 2 10 x 1) 4
5x 2
y2 3y 2 0
( y 1)( y 2) 0
5 x 10 x 5 0
2
y 1 or
x 2 2x 1 0
( x 1) 2 0
x 1
5(1) 1
2
2
(1)
3x 4 y 25 (1)
(3)
2
2
x y 25 (2)

2
2x 2
3x 2 0
3
From (1), we have
x2
9 x (4 x 8 x 4) 27 x 18 0
2
3 x 25
9 x 2 150 x 625
25
16
16 x 2 9 x 2 150 x 625 400
2( 2) 2
2
3
7
By substituting x
into (3), we have
13
7
2
2
4
13
3
13
y
25 x 2 150 x 225 0
x 2 6x 9 0
( x 3) 2 0
x 3
4
7
,
.
13
13
2) and
(1)
x 6 3( y 6) (2)
3
y2
2
x 2 y 2 936
(1)
From (2), we have

x 6 3 y 18
From (1), we have
3( 3) 25
4
4
21. From the question, we have
2 x 3xy 2 y 12 (2)
2
25
x2
19.
x2
7
x 2 or x
13
2x 3y 4 0
3 x 25
(3)
4
13 x 2 19 x 14 0
( x 2)(13x 7) 0
20. 3x + 4y = x2 + y2 = 25
From (1), we have
2x 2
3
3
( 2) 2 5
2
7
, 1 and (5, 2).
2
2
x y 3x 2 0 (2)
y
3
7
(1) 2
2
2
2x 3y 2
18.
y2
(3)
x 3 y 12 (3)

60

(3 y 12) 2 y 2 936
x 2 ( x 4) 2 400
9 y 2 72 y 144 y 2 936
x 2 x 2 8 x 16 400
10 y 2 72 y 792 0
2 x 2 8 x 384 0
( y 6)(10 y 132) 0
y 6 or y 13.2 (rejected)
x 2 4 x 192 0
( x 16)( x 12) 0
x 3(6) 12 30
The present ages of the father and his daughter are 30

and 6 respectively.
By substituting x = 16 into (1), we have y = 16 4 = 12

The lengths of the sides of square ABCD and square
DEFG are 16 cm and 12 cm respectively.
22. Let x cm and y cm be the lengths of the sides of the squares

ABCD and DEFG respectively.
EC = 4 cm
x
y4
23. Let x cm and y cm be the length and the width of the garden
respectively.
The area of the garden is 150 m2.
xy 150 (1)
The area of the path is 186 m2.
y x 4 (1)
The sum of their areas is 400 cm2.
[ x 2(3)][ y 2(3)] xy 186
x 2 y 2 400 ( 2)
xy 6 x 6 y 36 xy 186
6 x 6 y 150
x y 25
y 25 x (2)
x(25 x) 150
25 x x 2 150
x 2 25 x 150 0
( x 10)( x 15) 0
x 10 or x 15
y 25 10 15
y 25 15 10
The dimensions of the garden are 10 m 15 m.
24. Let x cm and y cm be the width and the length of each
y
x
The length of the wire is 78 cm.

10x + 12y = 78
y=
39 5 x
6
(1)
The area enclosed by the framework is 96 cm2.

8xy = 96
xy = 12
(2)
39 5 x
= 12
6
39x 5x2 = 72
5x 39x + 72 = 0
(x 3)(5x 24) = 0
x=3
or
x = 4.8
2
y=
61
39 5(3)
=4
6

By substituting x = 4.8 into (1), we have
2.
y=x+3
39 5( 4.8)
y=
= 2.5
6
x
y
1
2
0
3
1
4
The dimensions of each rectangle are 3 cm 4 cm or

4.8 cm 2.5 cm.
PS 2 AP 2 AS 2
25.
PS
( Pyth. theorem)
x 2 x 2 cm
2 x cm
PQ 2 BP 2 BQ 2
PQ
y y
2
( Pyth. theorem)
cm
2 y cm
PS SR RQ QP
Perimeter of PQRS
2 PS 2 PQ
( 2 2 x 2 2 y ) cm
3.
2 2 ( x y ) cm

The solutions of the simultaneous equations are (0, 3)
and (3, 6).
y = 2x 1
x
y
2 2 ( x y ) 16 2
x y 8
y 8 x (1)
0
1
1
1
2
3
PS PQ
Area of PQRS
( 2 x )( 2 y ) cm 2
2 xy cm 2
2 xy 30
xy 15 ( 2)
x(8 x) 15
8 x x 2 15
x 2 8 x 15 0
( x 3)( x 5) 0
4.

y=x1
x
y
x 3 or x 5
y 83 5
y 853
x = 3, y = 5 or x = 5, y = 3
3
4
2
3
1
2
Exercise 9B (p. 9.18)

Level 1
1. y = 6
The straight line added should be a horizontal line passing
through (0, 6).

(1, 6) and (3, 6).
62

4) and (1, 0).

5.
y = 2x 6
x
y
6.
1
4
x
y
2
2

y
x
y
7.
0
6
1
x2
2
2
3
0
2
9.
2
0
The two graphs intersect at (0.8, 2.8) and (1.8, 0.2).

The solutions of the simultaneous equations are (0.8,
2.8) and (1.8, 0.2).
x
y
y=4
The straight line added should be a horizontal line passing
through (0, 4).
1
1
3x + 2y 2 = 0
2
1

(4.8, 4.4) and (1.3, 1.4).
0
2
0
1
1 2
The two graphs intersect at (0, 1) and (2.3, 2.4).

and (2.3, 2.4).
10. L: y = 2x
(1)
C: y = 2x2 + 1
(2)
2x 2x 2 1
2 x 2 2 x 1 0 (3)
Consider the discriminant of 2x2 2x + 1 = 0.
8.

xy=2
63
( 2) 2 4( 2)(1)
4


11. L: y = 1 2x
(1)
C: y = x2 x
(2)
15.
x 2 16 5 x y (1)
( 2)
9 y 5x
From (2), we have
y = 5x 9(3)
1 2x x2 x
x x 1 0 (3)
2
x 2 16 5 x 5 x 9
Consider the discriminant of x2 + x 1 = 0.
1 4(1)( 1)
2
x 2 10 x 25 0
( x 5) 2 0

The simultaneous equations have 2 distinct real
solutions.
There are 2 intersections between the two graphs.
x5
x2 10x + 25 = 0 has one double real root.

The simultaneous equations have one real solution.
Level 2
16. y = x2 + 1
12. L: 7x + y = 3
(1)
C: y = 4x2 +5x 6
(2)
x
y
7 x 4x 2 5x 6 3
2
5
1
2
0
1
2
6
3
10
1
2
2
5
3
10
y = 4x 2
4 x 12 x 9 0 (3)
2
x
y
Consider the discriminant of 4x 12x + 9 = 0.
( 12) 2 4( 4)(9)

There is 1 intersection between the two graphs.
1
2
2
13. 3 x y 2 x 10 (1)
y 9x 8
( 2)
3 x (9 x 8) 2 x 2 10
2 x 2 12 x 18 0
x2 6x 9 0
( x 3) 2 0
14.
x3
x2 6x + 9 = 0 has one double real root.

The simultaneous equations have one real solution.
y 1 x 2 x (1)
( 2)
2x y 3

(1, 2) and (3, 10).
17. y = x2 1
x
y
From (2), we have y = 2x + 3(3)

2x 3 1 x 2 x
2
3
1
0
0
1
2
2
3
4
y = 2x 2
x
y
x x40
2
Consider the discriminant of x + x 4 = 0.

= 12 4(1)(4) = 17 > 0
x2 + x 4 = 0 has two real roots.
The simultaneous equations have two real solutions.
64
1
0
1
0
2
3
3
8
The two graphs intersect at (1, 0).

18. y = x2
x
y
3
9
2
4
1
1
4x + y + 5 = 0
x
3
2
y
7
3
1
1
0
0
1
1
2
4
The two graphs intersect at (0.7, 0.1) and (1, 1).

(0.7, 0.1) and (1, 1).
20. (a) y 4 x k
(1)
2
y 2 x 4 x 1 ( 2)

4 x k 2 x 2 4 x 1
2 x 2 8 x ( k 1) 0 (3)
The quadratic curve y 2 x 2 4 x 1

touches the line y 4 x k at one point.
0
82 4( 2)(k 1) 0
64 8k 8 0
8k 56
k 7
(b) By substituting k = 7 into (3), we have

2 x 2 8 x (7 1) 0

x2 4x 4 0
( x 2) 2 0
19. y = x2 x 1
x
y
2
5
1
1
0
1
0.5
0
1
1
1
1
2
1
x 2
By substituting x = 2 and k = 7 into (1), we have
3
5
y 4( 2) 7 1
2x + 3y = 1
x
y
2
1
21. (a)
The coordinates of P are (2, 1).
y 2x2 4x c
y 2x 7
(1)
( 2)
2x 7 2x 2 4x c
2 x 2 6 x (c 7 ) 0 (3)
65

solution.
( 6) 4( 2)(c 7) 0
2 4( k )(2) 0
36 8c 56 0
8c 20
5
2
24. y x k (1)
5
(b) By substituting c into (3), we have
2
5
2x 2 6x 7 0
2
9
2x 2 6x 0
2
2
4 x 12 x 9 0
y mx
m 2 4k
Revision Exercise 9 (p. 9.22)

Level 1
, 4 .
1.
22. 2 x y k 0
(1)
y x 8 x 9 ( 2)
y x 2 10 x 30 (1)
(2)
y 4 x 19
4 x 19 x 2 10 x 30
From (1), we have
y 2x k
x 2 14 x 49 0
(3)
( x 7) 2 0
x7
2 x k x 2 8x 9
x 10 x (k 9) 0
2
(4)
y 4(7) 19 9
The simultaneous equations have real solutions.
( 10) 4(1)(k 9) 0
100 4k 36 0
4k 64
k 16
2
23.
2.
2
y kx 3x 2
x 2 (2 x 1)2 1
5x 2 4 x 0
x(5 x 4) 0
(1)
( 2)
x 0 or x
kx 2 x 2 0
4
5

y 2(0) 1 1
x 4 kx 2 3 x 2
x 2 y 2 1 (1)
y 2 x 1 ( 2)

2
x2 4 x 2 4 x 1 1
y x4
( m) 4(1) k 0
2
From the graphs, y = mx has positive slope.

m>0
Let m = 8, then k = 16.
Let m = 4, then k = 4.
Let m = 2, then k = 1.
Possible values of m and k are:
m = 8, k = 16 or m = 4, k = 4 or m = 2, k = 1.
(or any other reasonable answers)
( 2)

x2 + k = mx
2
x mx + k = 0(3)
The simultaneous equations have only one solution.
(2 x 3) 2 0
3
x
2
3
By substituting x
into (2), we have
2
3
y 2 7 4
2
8k 4
1
k
2
(3)
4
into (2), we have
5
4
3
y 2 1
5
5
By substituting x
The line y = x + 4 does not intersect the quadratic

curve y = kx2 + 3x + 2.
66
4
3
, and (0, 1).
5
5
3.
3x 2 4 y 2
2x 2 y 9
Consider the discriminant of 3 x 2 4 x 16 0 .
( 4) 2 4(3)(16)
(1)
( 2 )
From (2), we have
9 2x
2
(3)
4.
9 2x
3x 2 4
2
2
3x 2 18 4 x 2
176
0
3 x 2 4 x 16 0 has no real roots.
x( x 3 y ) 4 y 2
x 2y 6
(1)
( 2)
From (2), we have

x 6 2 y (3)
(6 2 y )(6 2 y 3 y ) 4 y 2
3 x 4 x 16 0
2
(6 2 y )(6 y ) 4 y 2
36 6 y 2 y 2 4 y 2
6 y 2 6 y 36 0
y2 y 6 0
( y 2)( y 3) 0
y 2 or
y 3
By substituting y 2 into (3), we have
x 6 2( 2) 2
x 6 2( 3) 12
5.
x
y
1
0
0
1

and (12, 3).
y x 1
1
2
6.
67

(1, 0) and (4, 5).
y 2x 8
x
0
y
8
1
6
2
4

8.
(a)
y ( x 1) 2
x
y
7.
2
9
1
4
0
1
1
0
2
0
1
1
2
1
3
4
4
9
The two graphs intersect at (0.5, 7) and (5.5, 3).

(0.5, 7) and (5.5, 3).
(a) y = x2 + 2x
4
8
x
y
3
3
0
0
1
3
2
8
3
15
(b)
(c) (i)
4 y 20 x 9
x
1
2
y
2.8
7.8
3
12.8
(Note: The values of y are correct to the nearest 0.2.)

The two graphs intersect at (1.5, 5.2).
The solution of the simultaneous equations
is (1.5, 5.2).
(ii) y x 12
x
4
0
3
y
8
12
15
(b) (i)
y
x
y
The two graphs intersect at (4, 8) and

(3, 15).
The solutions of the simultaneous equations
are (4, 8) and (3, 15).
(ii)
68
1
x
2
0
0
2
1
4
2
The two graphs intersect at (0.5, 0.3) and

(2, 1).
are (0.5, 0.3) and (2, 1).
y 4 x
1
2
4
24

x
y
9.
2
8.5
1
4.5
0
0.5
10.
The two graphs intersect at (1.7, 7.3) and

(0.3, 1.7).
are (1.7, 7.3) and (0.3, 1.7).
(1)
y x 1
2
y 3 x x 4 (2)
From (1), we have
y x 1 (3)
x 1 3x x 2 4
x 2 4x 3 0
y 2 x 2 x 1 (1)
( 2)
2x y 3
Consider the discriminant of x 2 4 x 3 0 .
( 4) 2 4(1)(3)
From (2), we have

y 2 x 3 (3)
2x 3 2x 2 x 1
2 x 2 3x 4 0
Consider the discriminant of 2 x 2 3 x 4 0 .
11.
( 3) 4( 2)(4) 23 0
2
2 x 2 3 x 4 0 has no real roots.
0
x 2 4 x 3 0 has two distinct real roots.
The simultaneous equations have 2 real solutions.
x 2 4 y 2 20 0 (1)
( 2)
x 3y 5 0
From (2), we have
x 5 3 y (3)
(5 3 y ) 2 4 y 2 20 0
25 30 y 9 y 2 4 y 2 20 0
5 y 2 30 y 45 0
y2 6 y 9 0
( y 3) 2 0
y 3
y 6 y 9 0 has one double real root.

2
12. Let x be the present age of the younger brother and y be the
present age of the older brother.
The older brother is twice as old as the younger
brother.
2x y (1)
After four years, the sum of the squares of their ages
is 277.
( x 4) 2 ( y 4) 2 277
x 8 x 16 y 2 8 y 16 277
2
x 2 y 2 8 x 8 y 245 0
(2)
x 2 (2 x) 2 8 x 8(2 x) 245 0
5 x 2` 24 x 245 0
( x 5)(5 x 49) 0
x 5 or x
49
(rejected)
5

y 2(5) 10
The present ages of the brothers are 5 and 10.
69

13. (a) Let y cm be the length of a side of the square.
The perimeter of the rectangle is 18 cm greater
than that of the square.
1 2x
x 1
3
3x 2 1 2 x 3x 3
x2
2(4 x ) 4 y 18
8 2 x 4 y 18
x 2y 5
3x 2 5 x 2 0
(3x 1)( x 2) 0
x 5 2 y (1)
The rectangle and the square have equal areas.
4x y2 (2)
1
or x 2
3
1
By substituting x
into (3), we have
3
x
4(5 2 y ) y 2
y 2 8 y 20 0
( y 10)( y 2) 0
1
1 2
5
3
y
3
9
y 10 or y 2 (rejected)
The length of a side of the square is 10 cm.
(b) By substituting y 10 into (1), we have
x 5 2(10) 25
14. (a)
The length of the string is 14 cm.

PT TQ 14 cm
x y 14
PT 2 TQ 2 PQ 2
x y 10
2
(Pyth. theorem)
16.
x 2 y 2 100
The required simultaneous equations are:
2y 1 0
(1)
3
( x y )( x 2 y ) 2 (2)
(6 y 3 y )(6 y 3 2 y ) 2
(5 y 3)(8 y 3) 2
(b) From (1), we have

x y 14
40 y 2 39 y 9 2
y 14 x (3)
x 2 (14 x) 2 100
40 y 2 39 y 11 0
Consider the discriminant of 40 y 2 39 y 11 0 .
( 39) 2 4( 40)(11)
x 2 196 28 x x 2 100
239
0
2 x 2 28 x 96 0
x 14 x 48 0
( x 6)( x 8) 0
2
x 6 or x 8
By substituting x 6 into (3), we have y 14 6 8
17.
x6
x8
or
.
y 8
y6
The solutions are
2
15. x y x 1 (1)
2x 3y 1
( 2)
From (2), we have y
40 y 2 39 y 11 0 has no real roots.

(1)
pq60
3 p p 1 q 4 0 (2)
From (1), we have

q p 6 (3)
Level 2
1 5
, and (2, 1).
3 9
From (1), we have

x 6 y 3 (3)
(1)
x y 14
2
2
x y 100 (2)
1 2( 2)
1
3
1 2x
(3)
3
70

By substituting p 3.44 into (3), we have
q 3.44 6 2.56
By substituting p 0.77 into (3), we have
q 0.77 6 6.77
(3.44, 2.56) and (0.77, 6.77).
18. y x2 x
x 2 1
y
6
2
2x 3y 1
x
y
1 0.5
1 0
0
0
1
0
2
2
3
6
2
1
p
1 ( p 6) 4 0
4
3 p
3 p( p 4) 4( p 6) 16 0
3 p 2 12 p 4 p 24 16 0
3p2 8p 8 0
p
8 8 2 4(3)(8)
2(3)
8 160
6
3.44 or 0.77 (cor. to 2 d.p.)
71

(0.2, 0.2) and (1.4, 0.6).

21.
19. y x2 4x 3
x
y
0
3
2
0
1
0
2
1
3
0
4
3
(1)
y 4x c
2
y 4 x 7 x 3 (2)
x y
1
2 3
x
y
0
3
(a)
4
3
4x2 7 x 3 4x c
4 x 2 3 x (c 3) 0
(3)
The simultaneous equations have two real

solutions.
( 3) 4( 4)(c 3) 0
9 16c 48 0
16c 57
57
c
16
(b) (i)
By substituting (1, 6) into (1), we have

6 4(1) c
c2
(ii) By substituting c 2 into (3), we have
4 x 2 3x (2 3) 0
4 x 2 3x 1 0
(4 x 1)( x 1) 0
1
or x 1 (rejected)
4
1
By substituting x
and c 2 into (1), we
4
x
The two graphs intersect at (0, 3) and (2.5, 0.8).

and (2.5, 0.8).
have
y 2 x k 2 (1)
20. (a)
2
y x 6 x 6 ( 2)
y 4 2 1
4
x 2 6x 6 2x k 2
x 2 8 x (8 k ) 0
1
, 1 .
4
(3)
22. (a)
The quadratic curve touches the line at one point.

0
( 8) 2 4(1)(8 k ) 0
64 32 4k 0
32 4k 0
k 8
(b) By substituting k 8 into (3), we have
The y-intercept of the graph of

y ax 2 bx c
is 4.
c4
The x-intercepts of the graph of

y ax 2 bx 4 are 3 and 1.
0 a ( 3) 2 b( 3) 4
0 9a 3b 4
(1)
and 0 a (1) b(1) 4

2
x 2 8 x [8 ( 8)] 0
0ab4
x 2 8 x 16 0
(2)
(1) + (2) 3:
0 9a 4 3a 3 4
( x 4) 2 0
12a 16
4
a
3
x4
By substituting x 4 and k 8 into (1), we have
y 2( 4) ( 8) 2 2
The coordinates of Q are
By substituting a
72
4
into (2), we have
3
4
b4
3
8
b
3
0
(b) By substituting a
4
8
, b and c 4 into
3
3
y ax2 bx c, we have
4 2 8
x x4
3
3
Solve the simultaneous equations:
4
8
y x2 x 4
3
3
x 2 y 8 0
(3)
( 4)
4
8
x 2 x 2 x 4 8 0
3
3
8 2 19
x
x0
3
3
8 x 2 19 x 0
x(8 x 19) 0
x 0 (rejected) or x
By substituting x
23.
19
8
19
into (4), we have
8
19
2y 8 0
8
45
y
16
The coordinates of P are
19 45
,
.
8 16
(1)
y mx 6
2
2
x y 20 (2)
x 2 ( mx 6) 2 20
x 2 m 2 x 2 12mx 36 20
( m 2 1) x 2 12mx 16 0
(12m) 4( m 1)(16) 0
2
144m 2 64 m 2 64 0
80 m 2 64 0
4
m2
5
73
(3)
The two graphs intersect at two points.

m is a negative integer.
The largest possible value of m is 1.

24.
2 x y 2 0 (1)
2
y 2 x x c ( 2)
2 x ( 2 x 2 x c) 2 0
2 x 2 x (2 c) 0 (3)

1 4( 2)(2 c) 0
2
1 16 8c 0
8c 15
c
25.
15
8
c is a positive integer.
c 1
(1)
y 2x c
2
y x 6 x 2 ( 2)
(b)
OA
x 2 6x 2 2x c
x 2 4 x (2 c) 0
27. (a)
(3)
Let the two solutions of the simultaneous equations be h

and k.
Then x h and x k are factors of (3).
x 2 4 x (2 c) ( x h)( x k )
x 2 ( h k ) x hk
By comparing the constant terms, we have

2 c hk
Both solutions are negative.
hk > 0
2c 0
c 2 ( 4)
The simultaneous equations have two solutions.
(3) has two real roots.
x
y
0
0
The sum of the lengths of its diagonals is 11 cm.

x y 11
The required simultaneous equations are:
11x x 2 30
x 2 11x 30 0
( x 5)( x 6) 0
x 5 or x 6
y 11 5 6 (rejected AC > BD)
y 11 6 5
x
6, y 5
1
.
4
x2
8
10
3.5
1
xy 15
2
xy 30
x (11 x ) 30
4 4(1)(2 c) 0
16 8 4c 0
c 2 (5)
5 y 3x
The area of the kite is 15 cm2.
y 11 x (3)
(or any other reasonable answers)

26. (a)
49 m (cor. to the nearest integer)

The distance between the summit and the place
where the rock lands is 49 m.
(b) From (1), we have

x y 11
From (4) and (5), possible values of c are 1 or
44 2 22 2 m
x y 11 (1)
( 2)
xy 30

The place where the rock lands is (44, 22).
20 30 40
2 4.5 16
28.
2y x 0
x
0 10 20 30
y
0 5 10 15
74
The length of the wire is 36 cm.

8 x 4 y 36
y 9 2 x (1)
The total surface area enclosed by the framework is
48 cm2.
2 x 2 4 xy 48 (2)

2 x 2 4 x(9 2 x) 48
2 x 2 36 x 8 x 2 48
x 2 6x 8 0
( x 2)( x 4) 0
x(50 x ) 576
By substituting x 2 into (1), we have y 9 2(2) 5

By substituting x 4 into (1), we have y 9 2(4) 1
29.
x 50 x 576 0
2
x2 x4
or
.
y 5 y 1
( x 18)( x 32) 0
x 18 or x 32
y 50 18 32
y 50 32 18
The dimensions of the new rectangular pizza are
18cm 32cm.
x y 21 (1)
The perimeter of square ABCD is 60 cm.
4 BC 60 cm
60
x2 y 2
4
x 2 y 2 152
(1)
From (1), we have y 50 x (3)

x 2 or x 4
The solutions are
x y 50
The original area of the rectangular pizza is 616 cm2.

The reduced area of the new rectangular pizza is
(616 40) cm2, i.e. 576 cm2.
(2)
xy 576
6 x 2 36 x 48 0
2( x y ) 2(22 28)
Multiple Choice Questions (p. 9.26)

1. Answer: D
x 2 y 2 225 ( 2)
y x 2 5 x 6 (1)
(2)
y 2x
From (1), we have y 21 x (3)


x 2 5x 6 2x
x 2 (21 x) 2 225
x 2 7x 6 0
( x 1)( x 6) 0
x 2 441 42 x x 2 225
x 1 or x 6
By substituting x 1 into (2), we have y 2(1) 2
By substituting x 6 into (2), we have y 2(6) 12
and (6, 12).
2 x 2 42 x 216 0
x 21x 108 0
( x 9)( x 12) 0
2
x 9 or x 12
y 21 9 12
y 21 12 9
30. (a)
2.
Answer: B
x 2 y 2 2x 2 y 8
x 2 y 2 8 (1)
2 x 2 y 8 ( 2)
x 9 , y 12 or x 12 , y 9
From (2), we have

y 4 x (3)
From the question, we have

y x 6 (1)
22
xy
(14) 2
and
7
xy 616 (2)
x 2 ( 4 x) 2 8
x 2 16 8 x x 2 8
8 x 24
x3
x( x 6) 616

x 6 x 616 0
( x 22)( x 28) 0
2
3.
y x2 a2
ax by 4

y 22 6 28
The dimensions of the new pizza are
22 cm 28 cm.
(b)
Answer: D
(1)
(2)
5 ( 2) 2 a 2
a2 9
The perimeter of the pizza remains unchanged.
a 3

75
2a 5b 4 (3)
By substituting a 3 into (3), we have
By substituting a 3 into (3), we have
2( 3) 5b 4
b 2
2(3) 5b 4
2
b
5
4.
a3, b
2
a 3 , b 2
5 or
Answer: C
From the question, we have
(1)
xy 120
x 2 y 1 ( 2)
(2 y 1) y 120
2 y y 120 0
( y 8)(2 y 15) 0
2
y 8 or y
15
(rejected)
2

x 2(8) 1
15
5.
Answer: C
(1)
y 4x
2
y x k ( 2)
x 2 k 4x
x 2 4x k 0
6.
(3)

solution.
0
( 4) 2 4(1) k 0
16 4k 0
k 4
Answer: A
y x 2 x c (1)
( 2)
y 1 x
1 x x2 x c
x 2 2 x (c 1) 0
(3)
The simultaneous equations have two distinct real

solutions.
2 4(1)(c 1) 0
4 4c 4 0
c2
7.
Answer: A
(1)
y 3 x 1
2
y x 4 x 5 ( 2)
76
x 2 4 x 5 3 x 1
x2 x 6 0
( x 3)( x 2) 0
x 3 or x 2
P lies in Quadrant II.
x-coordinate of P 2
y 3(2) 1 7
8.
From the graph, we can find that the x-coordinates of

the intersections of the straight line and the quadratic
curve are 1 and 2.
The solutions of the quadratic equation
x2 x 2 are 1 and 2.
Answer: A
x
y
2
0
0
2
2
4
x2 x 2
(1)
y 2x k 2
2
y x 6 x 6 ( 2)
x2 x 2
(b) (i)
x 2 6x 6 2x k 2
x 4 x ( k 8) 0
2
9.
y x2
(3)
y x2
The simultaneous equations have only one solution.

0
a 1, b 2
(ii) y = x + 2
( 4) 2 4(1)( k 8) 0
16 4 k 32 0
k 4
Answer: D
y x 2 ax b (1)
(2)
y mx c
x 2 ax b mx c
x 2 ( a m ) x (b c ) 0
(3)
The simultaneous equations have two real solutions.

( a m) 4(1)(b c) 0
From the graph, the x-coordinates of the intersections

of the straight line and the quadratic curve are 1
and 2.
(iii) Yes, she is correct. Since the x-coordinates of the
intersections of the straight line and the quadratic
curve are the x-coordinates of the solutions of the
simultaneous equations
(a m) 2 4(b c) 0
(a m) 2 4(b c)
10. Answer: B
x
y
(p.
(a) (i)
2
2
0
0
2
2
y x2
Investigation Corner
9.28)
y x2
The value of k is 2.
, the x-coordinates found in (ii) are
the solutions to the quadratic equation x2 x 2.
(ii)
(c) (i)
No, Bens method is not correct. He should use the

linear equation y x.
(ii) y = x
77
2x 2 x 6 0
(d) (i)
x
x2 3 0
2
3
x
x2 x 3 0
2
6 3x
x2 x
2
y x2 x
6 3x ,
y
2
From the graph, we can find that the x-coordinates of

the intersections of the straight line and the quadratic
curve are 1 and 2.
The solutions of the quadratic equation
x2 x 2 are 1 and 2.
i.e.
y x2 x
2 y 3x 6
Add the line 2y 3x 6.

2y + 3x = 6
x
y
2
6
0
3
2
0
From the graph, the solutions are x = 2 and x = 1.5.
(ii)
2x 2 x 6 0
x
x2 3 0
2
x
2
6
x
x2
2
x2 3
y x2
6x ,
y
2
i.e.
y x 2
2 y x 6
Add the line 2y + x 6.

2y + x 6
78
x
y
0
3
5
2
2
2
From the graph, the solutions are x = 2 and x = 1.5.
79

X y y X

Uploaded by

Copyright:

Available Formats

You might also like

X y y X

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

X y y X

Uploaded by

Copyright:

Available Formats

9 Simultaneous Equations, One Linear and One Quadratic

Review Exercise 9 (p. 9.4)

By substituting y = 2 into (1), we have

By substituting (1) into (2), we have

By substituting x = 2 into (2), we have

By substituting y = 2 into (2), we have

NSS Mathematics in Action 4B Full Solutions

2(3 x 2 y 30) (5 x 4 y 16) 0

By substituting x = 4 into (1), we have

Lets Discuss (p. 9.6)

Classwork (p. 9.17)

By substituting y = 2 into (1), we have

The two straight lines intersect at (5, 1).

(3) has two distinct real roots.

The two straight lines intersect at (1, 2).

(3) has one double real root.

9 Simultaneous Equations, One Linear and One Quadratic

Quick Practice 9.1 (p. 9.5)

Consider the discriminant of x2 4x + 5 = 0.

(3) has no real roots.

By substituting (1) into (2), we have

From (2), we have

By substituting x = 2 into (3), we have

The solutions of the simultaneous equations are (2, 2) and

Quick Practice 9.3 (p. 9.7)

From (2), we have

NSS Mathematics in Action 4B Full Solutions

The solutions of the simultaneous equations are

and (1, 1).

Quick Practice 9.4 (p. 9.8)

The above gives us a pair of simultaneous equations.

From (1), we have

Quick Practice 9.5 (p. 9.9)

The sum of the squares of the two digits is 73.

9 Simultaneous Equations, One Linear and One Quadratic

Quick Practice 9.6 (p. 9.13)

By substituting x = 8 into (1), we have

The two graphs intersect at (0.5, 1.8) and (3, 0).

The two graphs intersect at only one point (0, 1).

The two graphs do not intersect.

NSS Mathematics in Action 4B Full Solutions

The simultaneous equations have only one real

By substituting x = 6 into (3), we have

From (2), we have

9 Simultaneous Equations, One Linear and One Quadratic

By substituting (2) into (1), we have

By substituting y = 10 into (3), we have

The solution of the simultaneous equations is

The simultaneous equations have no real

(a) Perimeter of the smaller rectangle

The dimensions of rectangle are 10 cm 20 cm.

NSS Mathematics in Action 4B Full Solutions

Further Practice (p. 9.15)

Exercise 9A (p. 9.10)

The two graphs intersect at only one point (2, 1).

By substituting (2) into (1), we have

By substituting x = 1 into (2), we have y = 4(1) + 12 = 16