Differential Calculus

Differential calculus deals with functions. A function is a mathematical expression that states a relationship
between two or more variables, one of which is a dependent variable and the other(s) being independent
variable(s). The expression y = f (x) reads y is a function of x. This implies that given a value of x, y can
be determined. Thus, if C = 20,000 + 30Q gives the total cost C as a function of the quantity produced Q,
we can obtain the value of C for a given value of Q. Similarly, suppose a company produces two types of
typewriters, E: electrical and M: mechanical and its profit function is, say, p = 250E + 170M 5EM +
1750. Here, p is a function of two independent variables M and E.
The slope of a function measures how much the dependent variable changes for small changes in each of
the independent variables. If a function is linear in nature, a straight line function that is, the slope of the
function is constant at all points. However, for functions other than linear, it is necessary to specify at what
point is the slope to be measured since the slope will be different at different values of the independent
variable. If the dependent variable increases with small increases in independent variable, the slope is
positive and if it decreases with increases in independent variable, the slope is negative.

Discrete and Continuous Functions

A function is discrete if the independent variable may assume only discrete values, like quantity produced
can only be a discrete value. The function is continuous if the variable can assume fractional values as well.
It may be mentioned that an essential theoretical
requirement of differential calculus is that the
y
function should be continuous. In practical business
Positive slope
Zero slope
situations, they rarely are so but calculus can be
B K
s
applied if it can be fairly assumed that they are.
C
Negative slope
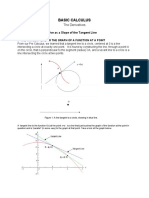
Now, assume that the graph of the function f (x)
A
we are considering is as shown in Fig. 1. Here the
r
A
curve is rising to a highest point K and is falling
f(x)
thereafter. Thus, K represents the maxima of the
curve. (In a similar manner, if a curve is first falling
to a point and then rising beyond it, then that point is
called the minima of the curve.).
o
A rising curve implies that its slope is positive
x
q xo
P
while a falling curve means a negative slope of it.
Fig. 1 Graphic Presentation of Function f (x)
Thus, the function f (x) is sloped positively to the left
of x0 and negatively to its right. At the point
established by x0, the slope is zero because here the
curve is neither rising nor falling.

Quantitative Techniques in Management

The slope refers to the rate of change of the dependent variable y, with respect to the rate of change of
the independent variable x. Conventionally, the rate of change is termed as slope when the change in x
equals one unit. Let us determine the rate of change between the points A and B in Fig. 1. We observe that
between these two points y increases from r to s, and x from p to q.
If we denote the change by D sign, we obtain the rate of change, or slope, as Dy/Dx = (s r)/(q p). This
rate of change is also known as the gradient of the function over this range, i.e. AB. In a similar manner, we
can find the slope between the points A and C, or between any pair of points for that matter. Clearly, the
slope as determined by Dy/Dx depends upon the interval of the function over which the measurements are
made and we can form as many Dy/Dx ratios as we care to select intervals.
In Fig. 1, the line and the curve between A and B, both start and finish at the same place but clearly the
line is a poor approximation of the curve. This approximation becomes gradually better as we select the
points closer to each other. Thus, although the ratio Dy/Dx is not an exact measure of the rate of change of
the function, we can obtain successively better estimates of it when Dx declines in value. Eventually, we
consider Dx so infinitesimal that the resultant rate of change, or the gradient, may be regarded as being the
gradient at a point rather than over an interval. In the figure we can represent it by line of practically no
length, say AA, which merely touches the curve at the point A and is called the tangent to the curve at the
point. The slope of AA is the gradient of the function at the point A and this is called the derivative or
differential coefficient. It is denoted by dy/dx.
To express the notion of the derivative mathematically, consider a small change in x, as Dx, and the
resulting change in y as Dy. Clearly, Dy represents the difference between the value of y at two successive
values of x, namely x and x + Dx. Therefore,
y = f (x + Dx) f (x)
and the gradient over the range is defined as

dy
f ( x + D x) - f ( x)
= Lim.
Dx 0
Dx
dx
That is, the derivative is the value of the expression when Dx approaches zero. To illustrate, suppose the
given function is y = 20x2. For this, we can determine the gradient as

F
GH
F 20x
= Lim. G
H

dy
20 ( x + D x ) 2 - 20x 2
= Lim.
Dx 0
Dx
dx

Dx 0

I
JK

+ 40x D x + 20( D x ) 2 - 20 x 2
Dx

I
JK

= Lim. (40x + 20Dx)

Dx 0

As Dx tends to zero, we have dy/dx = 40x because 20Dx would be practically equal to zero. The process
of determining the derivatives is called differentiation.

Techniques of Differentiation
We now state some basic rules used in differentiation. It may be mentioned here that the derivatives of a
function may be denoted either as dy/dx or as f (x).

Appendix A2: Differential Calculus

Constant Function If f (x) = c, where c is any constant, f (x) = 0. For example, if y = f (x) = 6, we have
f (x) = 0. If this function is plotted on a graph, we obtain a straight line parallel to the x-axis, which crosses
y at 6. The line, being parallel to the x-axis, has zero slope.
If f (x)= xn, where n is a real number, then f (x) = nxn 1

Power Rule
Examples

(a) f(x) = x7, f (x) = 7x6

(b) f(x) = 1/x7. Alternatively, f (x) = x 7.
f (x) = 7x 8 or 7/x8.

Thus,

(c) f(x) =

x 3 . Thus, f (x) = x3/4

f (x) =

Constant time function

have

3 1/4
3
x
= 4
4
4 x

If f (x) = c g (x), where c is a constant and g is a differentiable function, we

f (x) = c g (x).

Examples

(a) f(x) = 20x2, f (x) = 20(2x) = 40x

(b) f(x) = 5/x, f (x) = 5x 2 = 5/x2

Sum or Difference of Function

If f (x) = u(x) L(x), where u and L are differentiable,

f (x) = u(x) L(x)

Examples

(a) f (x) = 8x2 + 3x + 7, f (x) = 16x + 3.

(b) f (x) = 14x3 2x2 + 5/x3, f (x) = 42x2 4x 15/x4.

Product rule

If f (x) = u(x) L(x), where u and L are differentiable,

f (x) = u(x) L(x) + L(x) u(x).

Example 1 Given f(x) = (x3 6x2) (x + x4),

we have,

f (x ) = (x3 6x2) (1 + 4x3) + (x + x4) (3x2 12x)

= 7x6 36x5 + 4x3 18x2

The given function can, alternatively, be expressed as

f (x) = x7 6x6 + x4 6x3
Its derivative, using rule 4, is as follows:
f (x) = 7x6 36x5 + 4x3 18x2.
Quotient rule

If f (x) = u(x)/L(x), where u and L are differentiable, and L(x) 0,

f (x) =

L( x ) u ( x ) - u( x ) L ( x )
[ L ( x )]2

10

Quantitative Techniques in Management

Example 2

Given f (x ) = (4x2 7)/(2 x2). Find f (x).

f (x ) =

(2 - x 2 ) (8 x ) - (4x 2 - 7) (- 2 x )
(2 - x 2 )2
16 x - 8 x 3 + 8 x 3 - 14 x

x 4 - 4x 2 + 4

2x
4 + x 4 - 4x 2

Higher Order Derivatives

We have considered how the techniques of differentiation can be applied to a function f (x) in order to
obtain another function f (x).
Further, we can regard the function f (x) as being a function in its own right and can differentiate it. By
differentiating this function we get another function, denoted by f (x). For the given function 18x2 8x it
equals 36x 8. Since this is a derivative of a derivative, it is called the second derivative. Using the dy/dx
notation, this is expressed as d 2y/dx2 (pronounced as d two y by dx squared). The second derivative can
similarly be differentiated to get the third derivative, expressed as f (x) or d 3y/dx3. This process of
successive differentiation can be continued as long as the function remains differentiable. However, in
most cases, our interest lies only in the first and the second derivatives.
Example 3 Obtain all the derivatives of the following function:
y = 5x4 2x3 + 40
For this,

dy/dx = 20x3 6x2

d2y/dx2 = 60x2 12x
d3y/dx3 = 120x 12
d4y/dx4 = 120
d5y/dx5 = 0.

Maxima and Minima of Functions

In the minimum or maximum of a curve, the curve is neither rising nor falling and its gradient is zero.
Since the gradient is the same as the first derivative, the value of x for which the gradient is zero, represents
the presence of maxima or minima. In Fig. 1, we see that to the left of the maximum, the curve is rising and
has a positive gradient, while to its right it is declining and has a negative gradient. As we pass across the
maximum, the gradient of the function changes from positive to negative and therefore the gradient of the
gradient, that is, the change in the slope of the curve must be negative. Similarly, when we pass through the
minimum point of a curve, the gradient changes from negative to positive. Therefore, the change in the
slope must be positive. Obviously, then, the necessary conditions for maxima and minima are as follows:
For maxima,

dy
= 0,
dx

and

d2 y
d x2

<0

Appendix A2: Differential Calculus

dy
= 0,
dx

For minima,

d2 y

and

d x2

11

> 0.

Example 4 A large-sized company engages in door-to-door sales approach in a certain

metropolitan city. It observes that the sales response to the number of salesmen assigned follows
the law of diminishing returns. In particular, the company has found that the yearly profit earned P is
a function of the number of salesmen employed x, and the relationship is described by the equation
P = 10.5x2 + 627x + 205 (where P is given in hundreds of rupees). You are required to determine (a)
how many salesmen should be employed by the company to maximise the profit? (b) what is the
level of the maximum profit?

P = 10.5x2 + 672x + 205.

dP/dx = 21x + 672.

The given function is

For it,

Equating dP/dx = 0, we get 21x + 627 = 0, or x = 32.

Since the second derivative, d 2P/dx2 = 21 (a negative quantity) it implies that the function is
maximised at x = 32. Thus, when 32 salesmen are employed by the company, the profit earned would be
maximum.
At x = 32, the profit level would be:
P = 10.5 322 + 672 32 + 205 = 10,957 (hundred rupees).

Maxima and Minima in Functions of Several Variables

In case of functions involving two (or more) independent variables, changes in the dependent variable are
considered with respect to small changes in one of the independent variables, while others are held
constant. The process of differentiation is called partial differentiation. If y = f (x, z), the change in y with
respect to x alone is called a partial derivative of y with respect to x, and denoted by y/ x. The rate of
change of y with respect to z is denoted, similarly, by y/ z. The rule employed to compute partial
derivatives is to consider all the variables but the particular one under consideration as constant. To
illustrate, for the function y = 25x4 + 7z3 + 60xz 400, z would be considered a constant in calculating
y/ x, while x would be treated so in determining y/ z. Since the derivative of a constant is known to be
zero, we have, for the above function, y/ x = 100x3 + 60z, and y/ x = 21z2 + 60x. Partial derivatives are
in a sense, a special case of simple derivatives.
As with the function of a single variable, each of the function that we obtain may be differentiated
further. For instance, for the functions y/ x = 100x3 + 60z, and y/ x = 21z2 + 60x, we have
2 y/ x2 = 300x 2;
and
In general,

2y/ z 2 = 42z;

2y/ x z = 60; 2 y/ z x = 60.

2 y
2 y
=
x z
z x
We may now use these results to obtain the maxima or minima for a particular function. For a maxima,
y/ x = 0
and
y/ z = 0,

2 y
x2

< 0,

F yI F yI F y I
GH x JK GH z JK GH x z JK
2

and

2y/ z2 < 0

and
2

12

Quantitative Techniques in Management

For a minima,
y/ x = 0

2 y
x

y/ z = 0

and

>0

2 y

and

z2

F yI F yI F y I
GH x JK GH z JK GH x z JK
2

and

>0

Example 5 For a monopolist, selling two products A and B, the demand functions and the total
cost function are as given here. How many units of each of these products should he sell so as to
maximise his net profit? Also obtain the prices of each of the products and the value of the profit.

Demand functions
For product A,

PA + QA = 80

For product B,

PB + 2QB = 50.

Total cost function

TC = 14Q A2 + 4Q B2 + 8QA + 6QB + 4QAQB + 30.

According to the given information, total revenue would be:

TRA = 80QA Q 2A,
and
Total profit,

TRB = 50QB 2QB2

p = TRA + TRB TC
= 15Q 2A 6QB2 + 72QA + 44QB 4QA QB 30

p
= 30QA 4QB + 72 = 0
Q A
p
= 12QB 4QA + 44 = 0
QB
Rearranging these, and solving for QA and QB, we get QA = 2 and QB = 3. Here,

2 p
Q 2A

= 30,

and

and
However,

2 p
QB2

= 12 (both are negative)

2 p
=4
Q A QB

( 30) ( 12) > ( 4)2.

Thus, the monopolist would obtain maximum profit when QA = 2, and QB = 3 units. By substituting
these values in the profit function, we get p = 108. The price of A would be PA = 80 QA = 80 2 = 78, and
PB = 50 2QB = 50 6 = 44.