CIVL 2120

Mechanics of Materials

Ch. 3 Homework Problems

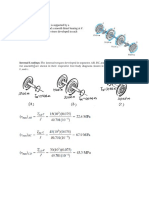
1. The electric motor exerts a torque

of 2.8 kNm on shaft AB. All shafts
are solid. Determine the maximum
sharing stress in shaft (a) AB, (b) BC,
(c) CD.

2. A motor exerts a torque of magnitude TF

at F. The shafts are made of steel
(allowable shear stress = 85 MPa) with
diameters dCDE = 22 mm and dFGH = 20
mm. If rD = 150 mm and rG = 100 mm,
determine the largest allowable value of TF.

3. Solid cylindrical rod BC is attached to rigid

lever AB and to a fixed support at C. The
vertical force P applied at A causes a small
displacement there. Show that the
corresponding maximum shearing stress in

the rod is = 2 , where d is the rod

diameter and G its modulus of rigidity.

4. The composite shaft shown consists of a 5mm-thick brass jacket (Gbrass= 39 GPa) bonded
to a 40-mm-diameter steel core (Gbrass= 77.2
GPa). Knowing that the shaft is subjected to a
600 Nm torque, determine (a) the maximum
shearing stress in the brass jacket, (b) the
maximum shearing stress in the steel core, (c)
the angle of twist of B relative to A.

5. At a time when rotation is prevented at the

lower end of each shaft, a 80-Nm torque is
applied to end A of shaft AB. Given G = 77.2
GPa for both shafts, determine (a) the
maximum shearing stress in shaft CD, (b) the
angle of rotation at A.

6. A torque T is applied to the solid tapered shaft AB

shown. Show that the angle of twist at A is
=

7
12 4

7. A steel pipe of 72-mm outer diameter is to be used to

transmit a torque of 2500 Nm without exceeding an
allowable shearing stress of 55 MPa. A series of 72-mmouter-diameter pipes is available for use. Knowing the wall
thickness of the available pipes varies from 4 mm to 10 mm in
2-mm increments, choose the lightest pipe that can be used.

8. The design of a machine element calls for a 40mm-outer-diameter shaft to transmit 45 kW. (a) If
the speed of rotation is 720 rpm, determine the
maximum shearing stress in shaft a. (b) If the
speed of rotation can be increased 50% to 1080
rpm, determine the largest inner diameter of shaft
b for which the maximum shearing stress will be
the same in each shaft.