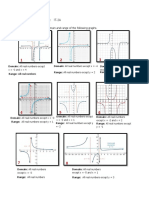
Exact

1st order ODEs

Tips and tricks

Might have to modify Yp if a term is

in Yh

, + ,
= 0

Exact if

Q =

. =

Variation of Parameters

General solution = I + J

=

1) Solve for I = 7 + <

= 7 < 7 <

How to Solve
1) , =
2) = ,
3)

,,.

J = 7 + <
Hyperbolic Function

4) Look at , to find ()
5) Find to find ,
6) If IVP solve for constant

Linear 2nd order nonhomogeneous

ODEs
Method Undetermined Coefficients
General Solution; y=Yh+Yp

+
2

If integral use substitution normally

making = () if one
substitution is required
Eg

U
Q = V7W

dx = 4 ()

Sub in for dx, 16 + 16 =

cosh

Roots of
2 roots 7 9: ; + < 9;=
9;

9;

+ <

Imaginary root
?; ( + )
=

Mass, Moments about axis and

Moments of Inertia
=
b

Needs to be calculated by
parametrising C in terms of single
variable .
;qr

;qs

Find Mass
Parametrise
Find Q .
Find

Q =

( < + < ) ,

If in form

f =

( < + < ) ,
( < + < ) ,

2D Line integral/work (Open C):

j

Check if F is conservative:
< 7
=

If conservative:
F =
Find f and apply the fundamental
theorem:

()

| p |

;qr

+ 2(()

1(()
;qs

2D Line integral/work (Closed C):

j

. =

Steps to solve
1)
2)
3)
4)

. = ()

If not conservative:

RQ

Q RQ
=

2

______________________________

1 root 7

<
=

Check if F is conservative:
< 7
=

If conservative:
j

. = 0

If not conservative:
Apply Greens Theorem:

=
.

Insure Greens theorem conditions

hold. Use the correct integral
bounds.
______________________________

2D Flux integral/flux (Open C):

.

Theres really nothing you can do

here.
Parametrise C p
Calculate n. T=

;
|

; |

left). If the divergence is 0, the

magnitude of flux across a curve is
the same as the flux across any
curve with those start and end
points (Compare to conservative
fields, line integrals and fundamental
theorem!)
______________________________
3D Line integral/work (Open C):

Txk / kxT = n
Note direction.
Evaluate the integral.

( ())
s

If C is very hard to parametrise, look

for another simple curve C1 such
that the union of C and C1 makes a
closed curve, C2. Then apply the flux
form of Greens theorem (Look
right).
Solve for the flux across C.

Check if F is conservative:
= = 0
If conservative:
F =
Find f and apply the fundamental
theorem:
j

.
j<

j7

2D Flux integral/flux (Closed C):

If not conservative:

3D Line integral/work (Closed C):

. =

Check if F is conservative:
= = 0
If conservative:

Note that if div(F) = 0, the flux is 0.

This can be used to calculate flux
across complicated open curves (see

Needs to be calculated by
parametrising C.

.
Use the flux form of Greens
theorem:

. =

(). | |

Insure Stokes theorem conditions
hold.
1)
2)
3)
4)

Parametrise S.
Calculate n.
Note direction.
Evaluate.

3D Flux integral/flux (Open S):

Nothing you can do.

Parametrise S.
Calculate n. Note direction.
Evaluate the integral.
If S is very hard to parametrise, look
for another simple surface S1 such
that the union of S and S1 makes a
closed surface, S2. Then apply
Gausss divergence theorem (Look
right).
Solve for the flux across C.
. =

.
<

Use Gausss divergence theorem:

. =

Note that if div(F) = 0, the flux is 0.

Moreover, if
=
the flux across any closed surface is
0 since div(F) = div(curl(G)) = 0. This
means the magnitude of the flux
across an open surface is the same
as the flux across any other surface
with the same boundary curve.
Fundamental theorem again!
______________________________
Surface Integrals

. = 0

If not conservative:

3D Flux integral/flux (Closed S):

. = ()

. =

Apply Stokes Theorem:

Surface area

Avg Vol over Surface

1

, ,

steps to solve
1) Parametrise ,
2)

,
,

,
,

3)
4)

Flux across a surface

=
b

( )du dv

PLU Decomp
Allowed to swap rows
1) R.e.f with swapping rows
2) = ,
det = det

Eigenvalues and Eigenvectors

1) det
2) for each , =
0
Diagonalisable
A is Diagonalisable if the
eigenvectors are linearly
independent
[1 2 3]
= p

det =
ODD NUMEBR OF ROW SWAPS =
-ve det

Terms- Orthogonally diagnosable IFF
its symmetry
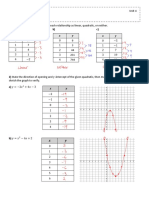
Quadratic equations and Conic
sections
< + < + + + +
= 0

LU Decomp

1) R.e.f
2) U=r.e.f, L=lower
3) Check A=LU
Not allowed to move rows
Given solve for =[b]
1) Sole LU
2) Set = =

3) Solve =

2
2

+
+ = 0

Diagonalising Quadratic
Forms/conic sections
Eg. Describe the conic section whose
equation is __________
Put in form

<

1) Eigenvalues
2) Eigen Vectors
3) Normalise

<

4) Create = [ p 1| p 2|3]
5) Create = p \
6) =

7) Set = = to get

values for , , in terms of

x,y,z

8) Set ; =

9) Solve
10) Sub in values of , ,
found in 7)
11) Complete the square
Power Method
Dominant Eigenvalue = highest ||
Dominant Eigenvector is the
corresponding vector with the
1)
2) = 7
3) 7 = <
4) Dominant Eigenvector is last
vector in sequence say
5) Dominant eigenvalue is
highest value in /
corresponding value in
Complex Matrices
Terms; =
1) Unitary Matrix- =
2) Hermitian
77
<7 +

7<
<<

3) Normal- =
Unitarily diagonalalisable
4) Det = 1=roatation Det = -1 =
reflection
Diagonalising a matrix
1)det ( ) solve for
2)Find vectors = 0
3)Form unitary matrix |7 7 |=P
= , = , =