CONTENTS CHAPTER PREVIOUS NEXT PREP FIND PROBLEM 02-0030: Solution: Mazarini Butchers, Inc., is a large-scale distributor of dressed meats which specializes in the hotel market and runs a highly technological operation. Schneider Hotels, Inc. placed an order for a ground meatloaf (mixed ground beef, pork, and veal) for 1,000 pounds according to the following specifications: a. The ground beef is to be no less than 400 pounds and not more than 600 pounds. b, The ground pork must be between 200 and 300 pounds. c. The ground veal must weigh between 100 and 400 pounds, 4d. The weight of ground pork must be no more than one and one half times the weight of veal The negotiated contract provides that Scheider Hotels will pay Mazarini Butchers $1,200 for supplying the meatloaf. ‘An analysis indicated that the cost per pound of beef, pork, and veal would be, respectively, $0.70, $0.60, and $0.80. The problem is one of maximizing contribution to overhead and profit subject to the specified constraints on flavor proportions and the demand constraint of 1,000 pounds. How can this problem be modeled? Can you suggest an easy solution? 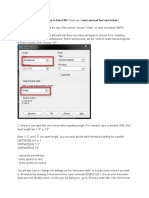Solution to Blending Problem xe 0 a ty 800 6) 109 «0 soo} SS “0 200 sh 13 5a WMS ‘ 100 is oy L x Let Too 700300 400-200-600 700 B00 900 Fig.1 x; = pounds of ground beef; x2 ounds of ground pork; xg = pounds of ground veal. At first, the problem appears to consist of three variables, which would make for a rather cumbersome graphical solution. The demandconstraint, however, allows for the tacit elimination of any one variable, say Xj that is Xq + Xp + xg = 1,000 may be rewritten as X3 = 1,000 — x4 — x. This expression may be substituted into the objective function and constraints wherever x3 appears. The complete problem may be stated as maximize: z = Revenue - Variable costs = 1,200 - 0.70x4 ~ 0.60xp - 0.80x3 = 1,200 - 0.70x4 ~ 0.60xp — 0.80 (1,000 - x4 — x9) = 400 + 0.10xy + 0.20x, subject to: x; $600 x1 2 400 (1) Xp $ 300 (2) X22 200 (3) x3 $400 (4) 1,000 - x4 - x $ 400 x1 + Xp 2 600 6) x3 2100 1,000 — x4 — x22 100 x1 + x2 S$ 900 6) Xq $ 1.5x3 Xp $ 1.5 (1,000 — xq — xg) 1.5x1 +2.5x2 $1,500 a) x4, Xp 20. Figure 1 is a graph for the seven constraints and the objective function. Note that constraints (5) and (6) are redundant constraints. Redundant constraints are those which contribute nothing to the determination of the solution space. The solution space is given by the polygon abode. The objective function has a slope of - (1/2) and is maximized at extreme point b. The coordinates (500, 300) for point b are determined from constraints (8) and (7). The optimal solution, therefore, is to send a meatloaf mixture consisting of 500 pounds of ground beef, 300 pounds of ground pork and 200 pounds of ground veal. The contribution to overhead and profit is maximized at 2 = 400 + 0.10(500) + 0.20(300) = $510.