520 Ch.

9 The Gutzwiller Variational Method

9.3 Brinkman-Rice Transition

The remaining task is to minimize the energy expression (9.44) with
respect to 7,which yields13

770= { 1 - u/ucr
+
1 U/Ucr
0
if 0 5 U

if U
5 U,,
> U,,
(9.45)

where the critical value of U is

Ucr = 81C1 . (9.46)

Replacing this in (9.34), we obtain

The salient feature of the solution is the prediction of a sharp metal-

insulator transition at T = 0. In a half-filled band, the charge carriers
are just the doubly occupied d, and the empty e sites. For U < Ucr
+
the density of charge carriers n d ne is finite, so we have a metal. For
U > U,,,n d + ne vanishes, so the system must be an insulator. The
Gutzwiller variational treatment gives a very simple scenario for a Mott
transition taking place within the paramagnetic phase, by ascribing it
to the gradual suppression of polarity fluctuations, i.e., of the density
of charge carriers.
The fact that the Gutzwiller method allows us to arrive at the result
(9.47),was pointed out by Brinkman and Rice [51]. Therefore we refer
to this particular description of the Mott transition as the Brinkman-
Race transition.
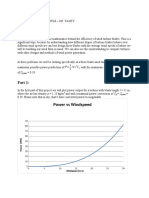
The n d versus U plot shows how the metallic nature is gradually
suppressed. It must be true that at the same time, the system becomes
I3Requiringd E ( q ) / d q= 0 would give just the first line of the expression. Formally,
nothing seems to prevent us from using it also for U > U,,,where q would become
negative. However, this would take us beyond the preset bounds of variation 0 5
Q _< 1. - There axe many ways to check that the 77 < 0 solution has to be rejected as
meaningless. For instance, n d would become negative.