Solutions to the Problems 191

We do not write down the cumbersome expression for the dispersion relation.
However, the reader will find it easy to check that the parametrization given
by Tasaki [392]
2, = q t - t‘) E = (A2 - 2)(t - t’) (4.78)
for arbitrary X simplifies the square root and leads to two cosine bands. Chos-
ing t’ < 0, the lower band has the dispersion 2t’cos k - 2(t - t’), while the
upper band follows 2t cos k + X2 (t - t’). It is curious that in spite of a non-zero
hybridmation, the shape of the two bands can be preserved.
At t’ = 0 the lower band becomes flat. In terms of Fig. 4.5, this is the
case of a “sawtooth lattice”.
b) The case E = 0, t’ = t can be conveniently reformulated (with t =
t‘ = -tl < 0 and Y = 4 2 ) as the tight binding chain with first- and second-
neighbour hopping

j o j o

Note that now the unit cell contains only one site. The dispersion relation is
given by
e ( k ) = -2t1 COBk - 2t2 cos 2k . (4.80)
cosk has one minimum for k E [-n,x],but cos2k has two. The same should
be true of e(k) if the second term is sufficiently strong. ~ ( k has
) extrema at
k = 0 and k = farccos(-tl/4t2). The two minima merge at k = 0 when
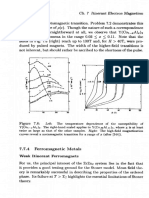
t 2 = -t1/4. e(k) has two minima if t 2 < -t1/4 (Fig. 4.13, left).

- en
-1.5 0 1 2

Figure 4.13: The dispersion relation of the t l - t 2 tight binding chain develops
two minima if 12 becomes sufficiently negative. Left: the dispersion relation for
t 2 = -0.6t1. Right: the DOS for t 2 = -tl (energy in units of t l ) .

Though at the first sight, this may look merely curious, at the second, it
should look alarming. There is a range of energies where the eigendues are
fourfold degenerate! If we think of e ( k ) as arising from solving the Schrodinger
eauation for a strictlv one-dimensional svstem. this is not allowed to hamen: