394 Ch.

7 Itinerant Electron Magnetism

of these developments is relevant for the understanding of iron. From

the point of view of many-body theory, we would like to have a lattice
model of interacting fermions, which resembles iron in essential respects,
shows ferromagnetism in a reasonable parameter range and it is simple
enough so that we can go beyond the mean field level and make sure
that ferromagnetism is a true feature of the model. The finding, and
solving, of such a model will provide the missing link between the LSDA
calculations, and the theory of correlation phenomena.

7.7.3 Nearly Ferromagnetic Metals

Materials for which I p ( q ~is) not much smaller than 1are near to satisfy-
ing the Stoner criterion38 (7.24) and can be called nearly ferromagnetic
metals (NFM). It means that the enhancement factor (1 - I p ( e ~ ) ) - l
appearing in the expression (7.23) for the spin susceptibility has a lar-
gish value thus we can alternatively speak about exchange enhanced
paramagnets (EEP) with a large enhancement factor3’.
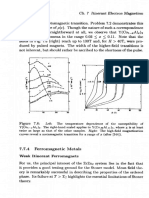
A well-known NFM is palladium. The temperature and pressure
dependence of the susceptibility is shown in Fig. 7.7. First of all, let us
observe that x is about an order of magnitude larger than that of simple
-
metals like potassium. LSDA gives I p ( e ~ ) .9and the calculated and
experimental values of x(T = 0) are fairly close [15]. Another notable
feature is that x(T)goes through a broad maximum around T 80K. N

We learn in Problem 7.1 (p. 406) that this can be accounted for as a
band structure effect: it arises if ~ ’ ’ ( is
qlarge
) enough, and the feature
is amplified by exchange enhancement.
Once a parameter is near a critical value, we are always interested
in possibilities of fine-tuning it. Applying pressure drives I p ( e ~ away
)
from 1: increased overlap widens the bands, and diminishes p ( e ~ ) Thus
.

rules) which was long suspected to be essential for ferromagnetism.

3 8 0 ~ derivation
r was formulated for the Hubbard model, and led to the enhance-
ment factor (1 - U p ( e ~ ) ) - ’ .We understand, however, that the Stoner mean field
theory applies to a wider class of models. Since in the present discussion, the Stoner
parameter usually characterizes a material rather than a model, we replace U by the
Stoner parameter 1.
30S~~ names
h
-
always have some ambiguity. We would say that W with its en-
hancement factor 5 is merely an EEP, not ‘‘nearly ferromagnetic”.