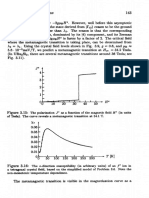
108 Ch.

3 Crystal Field Theory

eigenvalue as $. The question is whether x$

is really different from
(linearly independent of) $. The answer depends on the parity of n.
Denoting the unitary factor in (3.45)as
.
= eiqa,yeiqm,y . . eiqon.v (3.49)

Using now (3.48)

(3.51)

It follows that for odd n

(5$,$)
= 0. (3.52)
7$ and $ are orthogonal. Combining with (3.38), it means that we have
found an actual degeneracy: if $n is an energy eigenstate with eigenvalue
En,then x$n is another eigenstate with the same eigenvalue. Thus we
have proven
Kramers’ Theorem: if the Hamiltonian is time-reversal invariant
then the eigenstates of a system with an odd number of electrons are at
least twofold degenerate.
The theorem comes into its own in cases of low spatial symmetry.
The degeneracies we treated in the previous section resulted from the
rather high (for instance, cubic) symmetry of the crystal field. It stands
to reason that these degeneracies would be lifted by lowering the eym-
metry by further distortions. However, the electric fields described by
the crystal field Hamiltonian are time reversal invariant, thus Kramers
degeneracies cannot be removed by crystal fields, no matter how low
the symmetry is.
In the absence of spin-orbit coupling the statement can be regarded
as rather obvious: an odd number of electrons will necessarily have a
non-zero total spin “which can point either up or down”. It is important
to realize that Kramers’ Theorem holds also in the presence of spin-orbit
coupling because ‘Hfc~o= <S L is invariant under time reversal (since
both S and L get reversed). Taking one-electron states,

$1 +
= (P1 (r>a cpz(r)P