CONDITIONAL MEAN AND VARIANCE FORMULAE 𝑫𝒏 measures the maximum discrepancy between the sample

𝑬(𝑿) = 𝐸𝑌 [𝐸(𝑋|𝑌)] distribution function and the theoretical distribution

𝑬(𝑿𝟐 ) = 𝐸𝑌 [𝐸(𝑋 2 |𝑌)]
Law of Total Variance
𝑽𝒂𝒓(𝑿) = 𝐸𝑌 [𝑉𝑎𝑟(𝑋|𝑌)] + 𝑉𝑎𝑟𝑌 [𝐸(𝑋|𝑌)] 1.36
Critical Value at 5% significant level = , 𝑛 ≥ 15 (Klugman)
√𝑛
𝑑𝑥
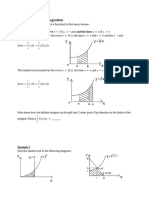
f ( x ) =  f ( x | y ) f ( y ) dy Transformation, 𝑔(𝑦) = 𝑓(𝑥)| 𝑑𝑦 |
y
This held IF the relationship between X and Y is monotonic
MOMENT AND CUMULANT GENERATING FUNCTIONS Jacobian Transformation (can be used to find marginal pdf)
M X ( t ) = E ( e Xt ) 𝑑𝑥1 𝑑𝑥1

K X ( t ) = ln M X ( t ) Where 𝐽 =
𝑑𝑦1
|𝑑𝑥2
𝑑𝑦2
det = ad-bc
𝑑𝑥2|,
  t t2
t 3

4
𝑑𝑦1 𝑑𝑦2
= ln e 1t 1 +  2 + 3 +  4 + ...   𝑔(𝑦1, 𝑦2) = 𝑓(𝑥1, 𝑥2)|𝐽|
  2! 3! 4! 
Masukin y2=x2 kalau ga dikasih.
where r is the rth central moment,
Careful masukin grafik
JOINT RANDOM VARIABLES Sum of Independent Random Variable
𝐶𝑜𝑣(𝑋, 𝑌) = 𝐸(𝑋𝑌) − 𝐸(𝑋)𝐸(𝑌) S = X +Y
𝐶𝑜𝑣(𝑋, 𝑌) s
𝝆= f S ( s ) =  f X ( s − y ) fY ( y ) dy
√𝑉𝑎𝑟(𝑋)𝑉𝑎𝑟(𝑌) 0
̂
Bayesian Estimate 𝜃𝐵 using prior & posterior distribution for
parameter. Equivalent 𝑃𝑜𝑠𝑡 𝐷𝑖𝑠𝑡. = 𝐿(𝜃) × 𝑝𝑟𝑖𝑜𝑟 𝑑𝑖𝑠𝑡 Pr ( S = s ) =  Pr ( X = s − y ) Pr (Y = y )
all y  s
▪ Square error/ quadratic loss = Mean Post Dist
▪ Absolute error loss = Median Post Dist. Risk premium: (lebih dari 1 polis) Expected claim cost for the
▪ All or nothing loss = Mode Post. Dist. respected party during a one year period. (Usually calculated in
Bayesian Interval = 𝑒𝑠𝑡𝑖𝑚𝑎𝑡𝑒 ± 𝑐𝑟𝑖𝑡𝑣. (𝑠𝑡𝑑𝑒𝑟𝑟), respect of all losses)
Conjugate Prior Excess of loss Reinsurance (per 1 polis):
(Poisson – Gamma) Mean amount payable by the reinsurer, in respect of all losses
∞
(Normal – Normal) ∫ (𝑥 − 𝐴)𝑓(𝑥)𝑑𝑥
Suppose we are estimating mean, where we already know the ∞
𝐴
variance. IF prior N(A,B), Posterior (C,D). 𝑥 is sample mean ∫ 𝑥𝑓(𝑥)𝑑𝑥 − 𝐴[1 − 𝐹(𝐴)]
𝑛𝑥𝐵 + 𝜎 2 𝐴 𝐴
𝐶= Mean amount paid by the insurer in respect all losses
𝑛𝐵 + 𝜎 2 𝐴
𝜎2 𝐵
𝐷= 𝐸(𝑋; 𝐴) = ∫ 𝑥𝑓(𝑥)𝑑𝑥 + 𝐴[1 − 𝐹(𝐴)]
𝑛𝐵 + 𝜎 2 0
(Gamma-Gamma) most likely Where the above integral can also be called as the limited expected
Check for bias, 𝐸(𝜃̂ ) = 𝜃 value function.
MLE Variance (Cramer-Rao bound for an unbiased estimator) If the underlying loss amount are increased by (1+r)% due to inflation
1 while the excess remains at A. The mean amount paid by the
𝑉𝑎𝑟(𝜃̂ ) = −
𝑑2 reinsurer in respect all losses will be
𝑛𝐸 [ 2 𝑙𝑛𝑓(𝑥; 𝜃)]
𝑑𝜃   A 
1 = (1 + r )  E ( X ) − E  X ; 
𝑉𝑎𝑟(𝜃̂ ) = − 2   1 + r 
𝑑
𝐸 [ 2 𝑙𝑛𝐿(𝜃; 𝑋)] ∞
𝐴
𝑑𝜃
= (1 + 𝑟) [∫ (𝑥 − )𝑓(𝑥)]
The expected is w.r.t X 𝐴 1+𝑟
1+𝑟
Maximum likelihood Interval Estimation If the excess also increased by A,
If normal, use normal
If approximate 95% confidence interval, use t (df n-1) for crit value (1 + r )  E ( X ) − E ( X ; A )
and cram-rao standard error. Mean Residual Life (per 1 polis)= The mean amount payable by the
TESTING FIT reinsurer in respect of claims made: (rata2 claim berapa). The
Chi-square Goodness of Fit test average over claims only (Excluding lossess less than $A)
∞
( observed − expected ) ∞ 𝑓(𝑥) ∫𝐴 𝑥𝑓(𝑥)𝑑𝑥
2
∫𝐴 (𝑥 − 𝐴) 1−𝐹(𝐴) 𝑑𝑥 , −𝐴
 =
2
1−𝐹(𝐴)
cells expected Mean Residual life Function
𝑓(𝐴) = 𝐸(𝑋 − 𝐴|𝑋 > 𝐴)
k
( fi − npi ) 2

= Taylor series Expansion

i =1 npi ∞
1
which for large n has an approximate  2 distribution with k − 1 1−𝑥
= ∑ 𝑥𝑛 , 𝑥(−1,1)
degrees of freedom 𝑛=0
∞
KOLMOGOROV-SMIRNOV TEST OF FIT 𝑥
𝑥𝑛
𝑒 =∑
𝑀𝑎𝑥 𝑛!
𝐷𝑛 = |𝐹𝑛 (𝑥) − 𝐹0 (𝑥)| 𝑛=0
𝑋 ∞
𝑥𝑛
𝑭𝒏 (𝒙) = 𝐸𝑚𝑝𝑖𝑟𝑖𝑐𝑎𝑙 𝑑𝑖𝑠𝑡 (𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑏𝑎𝑠𝑒𝑑 𝑜𝑛 𝑡ℎ𝑒 𝑠𝑎𝑚𝑝𝑙𝑒 𝑑𝑎𝑡𝑎)
ln(1 + 𝑥) = ∑(−1)𝑛−1 𝑜𝑟 𝑛+1 , 𝑥(−1,1]
𝑭𝟎 (𝒙) = 𝑇ℎ𝑒 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑖𝑚𝑝𝑙𝑖𝑒𝑑 𝑏𝑦 𝑛𝑢𝑙𝑙 ℎ𝑦𝑝𝑜𝑡ℎ𝑒𝑠𝑖𝑠 𝑛
𝑛=1