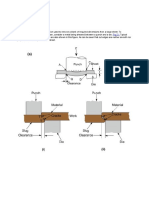
162 Sheet metal forming and blanking

Calculation of the blank size

Before starting drawing operations the size and form of the blank must
be determined for the desired final part geometry and die layout. This
should be shown using the example of a simple rotationally symmetrical
body. In order to calculate the blank diameter, it is necessary to devide the
entire axisymmetric part into various individual axisymmetric compo-
nents, in accordance with Table 4.2.1 and then calculate the surface areas
of these components. The total surface area as a sum of the individual
areas enables the calculation of the diameter of blank D. This is shown in
Table 4.2.1 for commonly used drawn shapes, starting from the desired
inner diameter d. As the material will be somewhat stretched in the draw-
ing process, there is more surplus material on the upper edge of the draw
part, which cannot be precisely calculated. With high parts this can lead
to distorted edges, because of the non-uniform deformation properties of
the blank material (anisotropy). Therefore, in general the drawn parts
must be trimmed accordingly on the edge, when produced via deep draw-
ing. The selection of the blank size for non-symmetric and irregular parts
is often carried out on a trial and error basis, as it is not possible to use
simple formulas. Based on practical experience, the blank geometry is
determined with experiments. Initially a sufficiently large blank size is
selected for the drawing operation. After observing the actual material
demand and flow, the blank size is reduced to satisfy the material
requirements. More recently, computer programs are being increasingly
used for the determination of the blank size (cf. Sect. 4.1.2).

Table 4.2.1: Formulas for the circular blank diameter D

Container shape (cross-section)

rotationally symmetrical shapes Blank diameter D =

1 d

d2 + 4 ⋅ d ⋅ h *
h

2 d2

d1 d 2 2 + 4 ⋅ d1 ⋅ h *

* Containers with small (bottom) radii r < 10 mm

Metal Forming Handbook / Schuler (c) Springer-Verlag Berlin Heidelberg 1998

Deep drawing and stretch drawing 163

Container shape (cross-section)

rotationally symmetrical shapes Blank diameter D =

3 d2

h2
d1 d 2 2 + 4 ⋅ (d1 ⋅ h1 + d 2 ⋅ h 2 ) *
h1

4 d3
h2

d2

d1
d 3 2 + 4 ⋅ (d1 ⋅ h1 + d 2 ⋅ h 2 ) *
h1

5 d2

d1 d 12 + 4 ⋅ d 1 ⋅ h + 2 ⋅ f ⋅ ( d 1 + d 2 ) *
f

6 d3
h2

d2
d1 d 2 2 + 4 ⋅ (d1 ⋅ h1 + d 2 ⋅ h 2 ) + 2 ⋅ f ⋅ (d 2 + d 3 ) *
h1

7 d

2 ⋅ d 2 = 1.414 ⋅ d

8 d2
d1

d 12 + d 2 2

9 d2
d1
1.414 ⋅ d12 + f ⋅ (d1 + d 2 )
f

10
d h
1.414 ⋅ d2 + 2 ⋅ d ⋅ h

* Containers with small (bottom) radii r < 10 mm

Metal Forming Handbook / Schuler (c) Springer-Verlag Berlin Heidelberg 1998

164 Sheet metal forming and blanking

Container shape (cross-section)

rotationally symmetrical shapes Blank diameter D =

11 d2

d1 h
d 12 + d 2 2 + 4 ⋅ d 1 ⋅ h

12 d2

1.414 ⋅ d12 + 2 ⋅ d1 ⋅ h + f ⋅ (d1 + d 2 )

d1 h
f

13 2
d

h
d2 + 4 ⋅ h2

14 d2
d1
d22 + 4 ⋅ h2
h

15 d2
d1
h2
h1
(
d 2 2 + 4 ⋅ h 12 + d 1 ⋅ h 2 )
16

( )
d h2
d 2 + 4 ⋅ h 12 + d ⋅ h 2
h1

17 d2

d 12 + 4 ⋅ h 2 + 2 ⋅ f ⋅ ( d 1 + d 2 )
d1
f h

18 d2

[ ]
d1
f
h2
h1
d12 + 4 ⋅ h12 + d1 ⋅ h 2 + 0.5 ⋅ f ⋅ (d1 + d 2 )

19 d2

d 12 + 2 ⋅ s ⋅ ( d 1 + d 2 ) *
d1

* Containers with small (bottom) radii r < 10 mm

Metal Forming Handbook / Schuler (c) Springer-Verlag Berlin Heidelberg 1998

Deep drawing and stretch drawing 165

Container shape (cross-section)

rotationally symmetrical shapes Blank diameter D =

20 d3
d2

d1 d 12 + 2 ⋅ s ⋅ ( d 1 + d 2 ) + d 3 2 – d 2 2 *
s

21 d2

[ ]
h
d1 d 12 + 2 ⋅ s ⋅ ( d 1 + d 2 ) + 2 ⋅ d 2 ⋅ h *
s

22
d2
d12 + 6.28 ⋅ r ⋅ d1 + 8 ⋅ r 2 or
d1 r
d 2 2 + 2.28 ⋅ r ⋅ d 2 – 0.56 ⋅ r 2

23 d3
d2 d12 + 6.28 ⋅ r ⋅ d1 + 8 ⋅ r 2 + d 32 – d 2 2 or
d1 r
d 32 + 2.28 ⋅ r ⋅ d 2 – 0.56 ⋅ r 2

24
d3
d2 d12 + 6.28 ⋅ r ⋅ d1 + 8 ⋅ r 2 + 4 ⋅ d 2 ⋅ h + d 32 – d 2 2 or
h
d1 r
d 32 + 4 ⋅ d 2 ⋅ (0.57 ⋅ r + h ) – 0.56 ⋅ r 2

25
d3
d2
d12 + 6.28 ⋅ r ⋅ d1 + 8 ⋅ r 2 + 2 ⋅ f ⋅ (d 2 + d 3 ) or

d1 r
f d 2 2 + 2.28 ⋅ r ⋅ d 2 + 2 ⋅ f ⋅ (d 2 + d 3 ) – 0.56 ⋅ r 2

26
d3
d2 d12 + 6.28 ⋅ r ⋅ d1 + 8 ⋅ r 2 + 4 ⋅ d 2 ⋅ h + 2 ⋅ f ⋅ (d 2 + d 3 ) or
h
f d1 r
d 2 2 + 4 ⋅ d 2 ⋅ (0.57 ⋅ r + h + 0.5 ⋅ f ) + 2 ⋅ d 3 ⋅ f – 0.56 ⋅ r 2

27
d2
h
(
d12 + 4 1.57 ⋅ r ⋅ d1 + 2 ⋅ r 2 + d 2 ⋅ h ) or

d1 r
d 2 2 + 4 ⋅ d 2 ⋅ (0.57 ⋅ r + h ) – 0.56 ⋅ r 2

* Containers with small (bottom) radii r < 10 mm

Metal Forming Handbook / Schuler (c) Springer-Verlag Berlin Heidelberg 1998