UNIVERSIDAD SAN FRANCISCO DE QUITO

COLEGIO POLITÉCNICO
ICV-0385 INGENIERÍA CIVIL HIDRÁULICA

LABORATORY #1
FLOW THROUGH AN ORIFICE
OBJECTIVES:
 To determine the discharge coefficient (çD), contraction coefficient (çc), and velocity coefficient (çv)
for the given orifice by the constant head method.
 To determine the real flow through a sharp edged orifice by measuring the drainage time for a given
volume of water.

EQUIPMENT REQUIRED:
 Supply tank with an Orifice  Weight Balance
 Point gauge for measuring jet trajectory  Rulers
 Collecting Tank  Water Pump
 Stopwatch  Hose

THEORY:
Orifice is a device which is used for discharging fluids from tanks. The tank is assumed to be
sufficiently large for the velocity of flow in the tank to be negligibly small except close to the orifice. In the
vicinity of the orifice, the fluid accelerates towards the center of the hole, so that as the jet emerges it suffers
a reduction of area due to the curvature of the streamlines. The reduction of area due to this local curvature
may be taken to be complete at about half the orifice diameter downstream of the plane of the orifice. The
reduced section is called the vena contracta.

For steady-state, frictionless flow of an incompressible fluid along a streamline, Bernoulli's equation states:

𝑃1 𝑣12 𝑃2 𝑣22
+ 𝑧1 + = + 𝑧2 +
𝛾 2𝑔 𝛾 2𝑔

In this equation the pressures P1 = P2 = Patm; velocity v1 is negligibly small, and z1-z2 = h. Hence we have:

𝑣22
ℎ=
2𝑔

Therefore, the velocity of fluid through the orifice is:

𝑣2 = √2𝑔ℎ

Velocity v2 is the theoretical velocity in the plane of the vena contracta. Because of the energy loss due to
friction effects, the real velocity vreal in the plane of the vena contracta will be less than v2.

EXPERIMENT DESCRIPTION:
Water enters the supply tank through a perforated diffuser placed below the water surface. The flow
passes into the tank and leaves through a sharp-edged orifice set at the side of the tank. Water from the
supply tank comes in the form of a jet and is directed into the collection tank. The volumetric flow rate is
measured by recording the time taken to collect a known volume of water in the tank. A horizontal scale,

Laboratorio de Hidráulica - LAB #1 1

 LABORATORY #1
ICV-0385 FLOW THROUGH AN ORIFICE HIDRÁULICA

with a gauge, mounted on to the inlet tank as shown in Fig. 1.1 is used to measure the x,y coordinates of an
imaginary point P along the jet of water. The gauge can be moved horizontally as well as vertically and its
corresponding movements can be read on the horizontal and vertical scales, respectively.

FORMULAS USED:

 CONSTANT HEAD METHOD

(a) Discharge Coefficient (çD)
Real Discharge Q 𝑟𝑒𝑎𝑙
𝜍𝐷 =
Theoretical Discharge Q 𝑡ℎ
Where,
Volume Collected
Real Discharge Q 𝑟𝑒𝑎𝑙 =
Time Taken

Theoretical Discharge Q 𝑡ℎ = 𝐴𝑜 √2𝑔ℎ

Ao = Area of the orifice, and

h = head of water level above the orifice.

Use this formula to calculate çD for each set of results obtained.

(b) Velocity Coefficient (çv)

Let x and y be the horizontal and vertical coordinates of the center line of the waterjet in relation to
the central point of the vena contracta, where the real velocity (vreal) of the jet can be calculated.
From the trajectory profile, the horizontal coordinate of any point P on the waterjet is:

𝑥
𝑣=
𝑡
𝑥
𝑡=𝑣 and hence,

The vertical coordinate of P (Fig. 1.1) is:

1 1 𝑥2
𝑦 = 2
𝑔𝑡 2 = 2 𝑔 𝑣2
Hence,
𝑔𝑥 2
𝑣𝑟𝑒𝑎𝑙 = √
2𝑦

The velocity coefficient çv can then be calculated as:

𝑔𝑥 2
𝑣𝑟𝑒𝑎𝑙 √ 𝑥
2𝑦
𝜍𝑣 = = =
𝑣𝑡ℎ √2𝑔ℎ 2√𝑦ℎ
Use this equation to calculate çv.

Laboratorio de Hidráulica - LAB #1 2

 LABORATORY #1
ICV-0385 FLOW THROUGH AN ORIFICE HIDRÁULICA

(c) Contraction Coefficient (çc)

Q 𝑟𝑒𝑎𝑙
𝐴𝑗𝑒𝑡 𝜍𝐷 𝐴𝑜 √2𝑔ℎ Q 𝑟𝑒𝑎𝑙 2𝑦 1/2
𝜍𝑐 = = = 𝑥 = [ ]
𝐴𝑜 𝜍𝑣 𝐴𝑜 𝑥 𝑔
2√𝑦ℎ

Use this formula to calculate çc for each set of results.

The observations required for the calculation of coefficients çD, çc and çv can be made simultaneously
with the measurements taken. The waterjet trajectory is obtained by measuring the horizontal distance x,
between the vena contracta of the waterjet and a point of the waterjet trajectory. Also note the vertical
distance y, between the center of vena contracta and the center of waterjet below. For the orifice, location
of the vena contracta from the edge for the small orifice can be taken as ½ of the diameter of the orifice.

PRECAUTIONS:

 Check that air is not trapped in the hose or pump before turning it on.
 Ensure water level is constant in the supply tank before taking any reading for constant head method.
 Use 2 decimal digits for measurements values.

PROCEDURE (LAB INSTRUCTIONS):

Determination of çD, çc, and çv using constant head method.

1. Fit a sharp-edged circular orifice of desired size to the opening in the side wall of the inlet tank, near
its bottom.
2. Ensure that air is not trapped in the hose or pump before turning it on.
3. Turn the pump on and adjust the flow rate using regulating valve so that the inlet tank is filled to the
height of the overflow pipe and steady discharge is obtained.
4. Measure the head “h” using the piezometric ruler fixed to the inlet tank.
5. Once the waterjet is steady, use a stopwatch for measuring the discharge. Meanwhile measure the
“x” and “y” distances. “y” may be measured from the center of the steady waterjet or may be
measured relatively by keeping offset from center.
6. Measure the real discharge by volumetric method. Volume of water may be calculated by measuring
the water depth in the collecting tank or by measuring the weight of water in the collecting tank.
7. Repeat this procedure for different height values of “h” ranging from 5 cm to 30 cm.

After entering the readings in the Tabulation 1.1, compute the necessary values.

PROCEDURE (Write down your own procedure report format)

POST-EXPERIMENT ACTIVITIES:

 The apparatus should be drained and cleaned after use.

Laboratorio de Hidráulica - LAB #1 3

 LABORATORY #1
ICV-0385 FLOW THROUGH AN ORIFICE HIDRÁULICA

Fig 1.1: Experimental setup for determination of coefficients of an orifice.

Laboratorio de Hidráulica - LAB #1 4

 LABORATORY #1
ICV-0385 FLOW THROUGH AN ORIFICE HIDRÁULICA

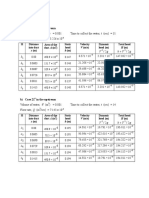
OBSERVATION AND COMPUTATIONS Date: ____________________

Diameter of the orifice D = ______________ cm. Area of the orifice Ao = _________________ cm2. NAME: _______________________________

Tabulation 1.1: Determination of the coefficient of discharge ҫD. by Constant-Head Method.

DISCHARGE DATA RESULT WATER JET DATA

Weight of Water Time Volume Theoretical 𝑥
No. h Real Discharge Q 𝑟𝑒𝑎𝑙 Error cD x y 𝜍𝑣 = Q 𝑟𝑒𝑎𝑙 2𝑦 1/2
in collecting Tank Taken Collected Discharge (mL/s) 𝜍𝐷 = 𝜍 = [ ]
(cm) (grams) Qreal (mL/s) Q 𝑡ℎ (%) (cm) (cm) 2√𝑦ℎ 𝑐 𝐴𝑜 𝑥 𝑔
(sec) (cm3) Qth = Ao 2gh

Average Value of CD = ______________ Gravity g = ____________ cm/s2.

Average Value of Cv = ______________

𝐴𝑣𝑔. 𝐶𝐷
Average value of Cc = _______________ Verification: 𝐶𝑐 = = ________________
𝐴𝑣𝑔. 𝐶𝑣

Laboratorio de Hidráulica - LAB #1 5

 LABORATORY #1
ICV-0385 FLOW THROUGH AN ORIFICE HIDRÁULICA

RESULTS AND ANALYSIS:

 Collected volume is determined by multiplying the area of the collecting tank (AT) by the water depth in
collecting tank “R”; or by taking the weight of the collected water divided by the density of water.
 The Real Discharge is calculated by dividing the collected volume by the time taken to collect such volume.
 After you have calculated all of the coefficients çD, çc and çv for each run, determine the average value for the
coefficients çD, çc and çv.
 An operational error of your calculation can be obtain by comparing the average value of çc versus the
calculated value of çc obtained by dividing the average value of çD by the average value of çv. Explain.
 Analyze and explain the results and calculations obtained from your lab experiment. For example, explain
extreme values (min. & max) in your results. Justify causes and explain the consequences.

GRAPH:

Use measurements observed during the constant-head experiment to graph the following:

1. Plot Qth, Qreal vs. h are drawn by taking h on x-axis, and Qth , Qreal on y-axis. (1 graph)
2. Plot çD vs. Qreal, Qth, is drawn taking çD on x-axis, and Qreal, Qth, on y-axis. (1 graph)
3. Plot çc vs. çv, is drawn taking çc on x-axis and çv on y-axis.
4. Plot X vs. Y, where the y-axis should be an inverted axis. Include the point X=0, Y=0, in your data;
and fit a parabolic curve to the data points. Determine the equation of the waterjet trajectory.
 For each graph, plot points for each trial experiment, then fit a line for the overall tendency.
 Discuss and explain the meaning of each graph.

DISCUSSION:

 Discuss assumptions of the theory applied in this lab practice.

 Discuss the accuracy of each result, numerically. Identify the possible experimental errors.
 Calculate the bias error for each run based on the deviation from the true value of the discharge coefficient, çD.
 Analyze the probable sources of error and explain how much error generates the uncertainty on consequence.

 QUESTIONS:
1) Why do we need to understand and analyze the behavior of an orifice flow? What is the purpose of an
orifice and where do you use them in the practical life?

2) What is the distance at which the vena contracta occurred during the experiment? What is the
relationship between CD, Cc and Cv. Calculate the actual flow area of the Vena Contracta.

3) Explain each of the energy components for the assumed initial conditions for the water surface.

4) What are Orifice Plates and what are they used for?

5) Explain how the discharge coefficient, çD accounts for the friction energy losses hf?

Laboratorio de Hidráulica - LAB #1 6