Mathematics SL

ALGEBRA
Worksheet 1

1. In an arithmetic sequence, u1 = 2 and u3 = 8.

(a) Find d.
(2)
(b) Find u20.
(2)
(c) Find S20.
(2)
(Total 6 marks)

2. Let f(x) = 3 ln x and g(x) = ln 5x3.

(a) Express g(x) in the form f(x) + ln a, where a  +
.
(4)

(b) The graph of g is a transformation of the graph of f. Give a full geometric

description of this transformation.
(3)
(Total 7 marks)

3. In an arithmetic sequence u1 = 7, u20 = 64 and un = 3709.

(a) Find the value of the common difference.
(3)

(b) Find the value of n.

(2)
(Total 5 marks)

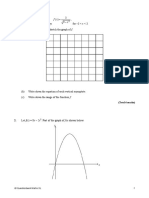
x
4. Let f(x) = log3 + log3 16 – log3 4, for x > 0.
2
(a) Show that f(x) = log3 2x.
(2)

(b) Find the value of f(0.5) and of f(4.5).

(3)

ln ax
The function f can also be written in the form f(x) = .
ln b
(c) (i) Write down the value of a and of b.

(ii) Hence on graph paper, sketch the graph of f, for –5 ≤ x ≤ 5, –5 ≤ y ≤ 5,

using a scale of 1 cm to 1 unit on each axis.

(iii) Write down the equation of the asymptote.

(6)

(d) Write down the value of f–1(0).

(1)

The point A lies on the graph of f. At A, x = 4.5.

(e) On your diagram, sketch the graph of f–1, noting clearly the image of point A.
(4)
 (Total 16 marks)

5. Consider the expansion of (x + 2)11.

(a) Write down the number of terms in this expansion.
(1)

(b) Find the term containing x2.

(4)
(Total 5 marks)

6. (a) Expand (2 + x)4 and simplify your result.

(3)

 1 
(b) Hence, find the term in x2 in (2 + x)4 1  2  .
 x 
(3)
(Total 6 marks)

7. Let f(x) = log3 x , for x > 0.

(a) Show that f–1(x) = 32x.
(2)

(b) Write down the range of f–1.

(1)

Let g(x) = log3 x, for x > 0.

(c) Find the value of (f –1 ° g)(2), giving your answer as an integer.
(4)
(Total 7 marks)

8. Solve log2x + log2(x – 2) = 3, for x > 2.

(Total 7 marks)

9. Consider the arithmetic sequence 3, 9, 15, ..., 1353.

(a) Write down the common difference.
(1)

(b) Find the number of terms in the sequence.

(3)

(c) Find the sum of the sequence.

(2)
(Total 6 marks)

10. An arithmetic sequence, u1, u2, u3, ..., has d = 11 and u27 = 263.
(a) Find u1.
(2)

(b) (i) Given that un = 516, find the value of n.

(ii) For this value of n, find Sn.
(4)
(Total 6 marks)