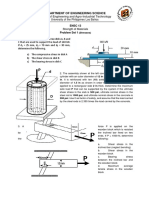
STRENGTH OF MATERIALS 2. Determine the tensile stress at the root of the bolt in MPa.

A. 131 B. 111 C. 97 D. 122

STRESS 3. Determine the compressive stress in MPa at the head as the bolt
SITUATION 1. The bar ABCD consists of three cylindrical steel bears on the surface to resist the tensile load.
segments with different lengths and cross sectional areas. Axial loads A. 49.4 B. 82.9 C. 44.9 D. 39.3
are applied as shown.
THIN WALLED PRESSURE VESSELS
SITUATION 6. A cylindrical steel pressure vessel 400 mm in diameter
with a wall thickness of 20 mm, is subjected to an internal pressure of
4.5 MN/m2.
1. Calculate the tangential stress in the steel. 45 MPa
2. Calculate the longitudinal stress in the steel. 22.5 MPa

1. Calculate the normal stress at segment AB. 3330 psi STRAIN

2. Calculate the normal stress at segment BC. 2780 psi
3. Calculate the normal stress at segment CD. 4380 psi
SITUATION 2. A hollow circular post ABC as shown in the figure
supports a load of P1 = 1700 lb acting at the top. A second load P 2 is
uniformly distributed around the cap plate at B. The diametes and
thickness of the upper and lower parts are dAB = 1.25 in, tAB = 0.5 in, dBC
= 2.25 in, and tBC = 0.375 in respectively.
SITUATION 7. The rigid beam AB shown in the figure below supports a
load W at B. The beam is hinged at A and supported by a steel cable
CD at C. The cable is The cable is 36 mm in diameter and is 3 m long.
Use E = 200 GPa. L1 = 1.8 m, L2 = 1.2 m. Neglect the weight of the
beam.

1. Calculate the normal stress AB in the

upper part of the post.
A. 1443 C. 1175
B. 1587 D. 1230
2. If it is desired that the lower part of
the post have the same compressive
stress as the upper part, what should be
the magnitude of the load P2 in lbs?
A. 1560 C. 1702
B. 1488 D. 1896 1. If W = 80 kN, what is the vertical deflection of point B in mm?
A. 1.96 B. 2.46 C. 3.64 D. 3.27
3. If P1 remains at 1700 lb and P2 is now 2. If the allowable stress of cable CD is 124 MPa, what is the maximum
set at 2260 lb, what new thickness of value of W in kN?
BC in inches will result in the same A. 75.73 B. 96.35 C. 102.54 D.163.24
compressive stress in both parts? 3. Find W in kN if the strain of cable CD is 0.002 mm/mm.
A. 0.85 C. 0.71 A. 200.7 B. 215.7 C. 189.3 D. 244.3
B. 0.63 D. 0.50
SITUATION 8. A steel rod having a cross-sectional area of 300 mm2 and
SITUATION 3. The uniform 2-Mg bar is a length of 150 m is suspended vertically from one end. It supports a
supported by a smooth wall at A and by a tensile load of 20 kN at the lower end. If the unit mass of steel is 7850
pin at B that is in double shear. Determine kg/m3 and E = 200 × 103 MPa, find the total elongation of the rod in mm.
the diameter of the smallest pin that can A. 43.5 B. 54.3 C. 35.4 D. 45.3
be used if its working shear stress is 60
MPa. 14.91 mm SITUATION 9. A steel bar 50 mm in diameter and 2 m long is surrounded
by a shell of cast iron 5 mm thick. Compute the load in kN that will
SITUATION 4. An angle bracket having a compress the bar a total of 1 mm in the length of 2 m. Use E of steel =
thickness t = 0.75 in is attached to the 200 GPa and E of cast iron = 100 GPa.
flange of a column by two 5/8-inch diameter bolts. A uniformly distributed A. 200 B. 240 C. 280 D. 320
load from a floor joist acts on top face of the bracket with a pressure p =
275 psi. The top face of the bracket has length L = 8 in and width b = 3.0 THERMAL STRESSES
in. SITUATION 10. The horizontal steel rod, 2.5 m long and 1200 mm2 in
cross-sectional area, is secured between two walls as shown in the
figure below. If the rod is stress-free at 20⁰C. Compute the stress when
the temperature has dropped to 20⁰C.
15. Assume that the walls do not move. 93.6 MPa
16. Assume that the walls move together a distance D = 0.5 mm. Use α
= 11.7 x 10-6 /⁰C and E = 200 GPa. 53.6 MPa

1. Determine the average bearing pressure in ksi between the angle

bracket and the bolts.
A. 11.65 B. 9.80 C. 8.35 D. 7.04
2. Determine the average shearing stress in ksi of the bolts. Disregard
friction between the bracket and the column.
A. 12.96 B. 8.82 C. 9.37 D. 10.76
TORSION
SITUATION 5. The bolt shown in the figure is subjected to a total tensile SITUATION 11. The figure below shows a 2-in.-diameter solid steel
force of 98 kN. cylinder that is built into the support at C and subjected to the torques TA
and TB.
17. Determine the maximum shear stresses in segments AB and BC of
the cylinder. 6880 and 3820 psi
18. Compute the angle of rotation of end A. Use G = 12 x 10 6 psi for
steel. 0.04584 rad or 2.63⁰

1. Determine the tensile stress in the body of the bolt in MPa.

A. 78.5 B. 68.8 C. 92.6 D. 86.4
SITUATION 12. A hollow circular bar with outside diameter of 110 mm HORIZONTAL SHEARING STRESS
and wall thickness of 6 mm is subjected to a torque of 12 kN-m. Use G SITUATION 19. Determine the maximum and minimum shearing stress
= 83 GPa. Length of the bar is 3.2 m. in the web of the wide flange section if V = 100 kN.

1. Calculate the torsional rigidity of the bar in KN-m2.

A. 441.4 B. 536.4 C. 487.9 D. 635.2
2. Calculate the torsional stiffness of the bar in kN-m/rad.
A. 132.85 B. 124.10 C. 104.87 D. 137.95
3. What is the maximum angle of twist in degrees?
A. 0.087 B. 8.69 C. 2.54 D. 4.98

POISSON’S RATIO
SITUATION 13. A 20-mm diameter steel rod, 250 mm long is subjected
to a tensile force of 75 kN. If the Poisson’s ration is 0.30, determine the
lateral strain of the rod. Use E = 200 GPa.
A. 3.581 x 10-4 C. -2.467 x 10-4
B. -3.581 x 10-4 D. 2.467 x 10-4 SITUATION 20. A uniformly distributed load of 200 lb/ft is carried on a
simply supported beam span. If the cross-section is as shown above,
SITUATION 14. A solid aluminum shaft of 100-mm diameter fits determine the maximum length of the beam if the shearing stress is
concentrically in a hollow steel tube. Determine the minimum internal limited to 80 psi. Assume the load acts over the entire length of the
diameter of the steel tube so that no contact pressure exists when the beam. 12.64 ft
aluminum shaft carries an axial compressive load of 600 kN. Assume
Poisson’s ratio equal to 1/3 and the E of aluminum be 70 GPa. HELICAL SPRINGS
A. 100.0364 C. 100.0303 SITUATION 21. Two close-coiled helical springs of the same length are
B. 100.0312 D. 100.0414 wound out of the same wire, circular in cross-section and supports a
compressive load P. The inner spring consists of 20 turns of mean
SHEAR FLOW diameter 16 cm and the outer spring has 18 turns of mean diameter 20
SITUATION 15. A steel tube (G = 76 GPa) has the cross section shown cm. Calculate the maximum stress produced in each spring if the
in the figure. The tube has a length L = 1.5 m and is subjected to a torque diameter of wire = 1 cm and P = 1000 N.
of T = 10 kNm. Answer: Inner spring = 267.8 MPa
Outer spring = 189.29 MPa

SITUATION 22. A rigid bar, hinged at one end, is supported by two

identical springs as shown in the figure. Each spring consists of 20 turns
of 10-mm wire having a mean diameter of 150 mm. Neglect the mass of
the rigid bar.

1. Calculate the shear stress.

A. 53 B. 35 C. 42 D. 48
2. Calculate the angle of twist in degrees.
A. 0.38 B. 0.57 C. 0.68 D. 0.71 1. Compute the maximum shearing stress in the left spring in MPa.
A. 7.74 B. 18.31 C. 16.62 D. 23.23
SHEAR AND MOMENT IN BEAMS 2. Compute the maximum shearing stress in the right spring in MPa.
SITUATION 15. Plot the shear and moment diagram of the beams A. 7.74 B. 18.31 C. 16.62 D. 23.23
below.
FLANGE BOLT COUPLING

SITUATION 23. A flanged bolt coupling consists of ten 20-mm diameter

bolts spaced evenly around a bolt circle 400 mm in diameter. Determine
the torque capacity in kN-m of the coupling if the allowable shearing
stress in the bolts is 40 MPa.
A. 26.87 B. 25.13 C. 24.69 D. 22.35

COMBINED STRESSES AND MOHR’S CIRCLE

MOVING LOADS
SITUATION 16. Three wheel loads roll as a unit across a 44-ft span. The
loads are P1 = 4000 lb and P2 = 8000 lb separated by 9 ft, and P3 = 6000
lb at 18 ft from P2.
23. Determine the maximum moment in the simply supported span. 127
636.4 lb-ft
24. Determine the maximum shear in the simply supported span. 14
318.2 lb
FLEXURAL OR BENDING STRESS
SITUATION 17. A simply supported beam, 2 in wide by 4 in high and 12
ft long is subjected to a concentrated load of 2000 lb at a point 3 ft from
one of the supports.
25. Determine the maximum fiber stress. 10 125 psi
26. Determine the stress in a fiber located 0.5 in from the top of the beam
at midspan. 5062.5 psi
SITUATION 22. A hollow circular pole, 6 mm thick with 300 mm outside
diameter and height of 3 m weighs 150 N/m. The pole is subjected to
the following loads:
Vertical load: P = 3 kN at an eccentricity of e = 100 mm from the centroid
of the section
Lateral load: H = 0.45 kN at the top of the pole
1. Determine the maximum compressive stress at the base due to the
loads. -4.67 MPa
2. Determine the maximum tensile stress at the base due to the loads.
3.59 MPa
SITUATION 23. If a point is subjected to
the state of stress as shown:
1. What is the maximum shearing stress?
50 MPa
2. What is the maximum principal stress?
60 MPa
3. What is the minimum principal stress? -
40 MPa

SITUATION 18. The simply supported beam in the figure below has the
T-shaped cross section shown. Determine the values and locations of
the maximum tensile and compressive bending
stresses.
Answers: δT = 2580 psi (bottom of the section at x = 4 ft)
δC = 3230 psi (bottom of the section at x = 10 ft)