Chapter 5 - Applications of Integration PDF

MAT183 – CALCULUS I
CHAPTER 5: APPLICATIONS OF INTEGRATION
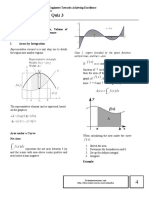
1. Sketch the graph (if graph is not given).
AREA 2. Find the boundary (upper limit and lower limit if not
BETWEEN Step to find given). So that, we can find the ucf and lcf by substitute
area using the value of x taken from the interval [a, b].
TWO integration:
CURVES Set up the integral.
Evaluate the integral.
Area Between Curves (Formula Area Between Curves (Formula

I) II)
• The area of • The area of

the region the region
bounded by bounded by
the curves the curves
y = f(x) x = f(y)
and y = and x =
g(x), and g(y), and
the line x the line y
= a and x = = c and y
b. = d
RCMN_JSM | MARCH - JULY 2019

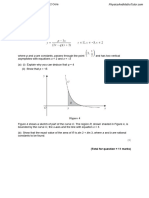
EXAMPLE OF PYQ (JUNE 2019)
Figure 2 below shows the region R bounded by the curve

x  y2  1 and the line x  7  y
a) Find the coordinates of M and N.

(2 marks)
b) Find the area of the shaded region R.
(4 marks)

EXERCISE 1
a) The region R is bounded by the curve y 2  1  x and the line

y  x 1
i. Find the coordinates of A and B.

ii. Find the area of the shaded region R.

b) Figure below show the region R which is bounded by the line

y  x  1 and the curve y  x  12. The coordinates of the
intersection between the line and the curve are (1,0) and
(2,1). Find the area of the region R.

c) The region R in following figure is bounded by the curve

y  x 2  2 and the line x  y  4.


d) The region R in Figure 3 is bounded by the curve

x  y2  4y  2 and the line x  y  2.


e) The shaded region is bounded by the curve y  x2  x  1 and

y  -x .

ii. Find the area of the shaded region.

f) The shaded region is enclosed by the curve y  4  x2 and

y  2x  4.

ii. Find the area of the shaded region.

g) Figure shows the curves y  x2  4x  3 and y  x2  2x  3

intersects at points A and B.


h) Figure shows the shaded region R bounded by the parabola

y 2  4x and the line x = 1.
i. Find the coordinates of P and Q.

ii. Determine the area of R.
10

i) Figure shows the region R by the curve y  x2 , the line

y  4 and y – axis.
i. Find the coordinates of A.

ii. Determine the area of R.
11

TUTORIAL
1. Figure shows the region bounded by the curve x  1  y - 22

and x = 2.
a) Find the coordinates of A and B.

b) Find the area of the shaded region.
2. Figure shows the region bounded by y  x2  4 and

y  4x  x 2  4 .
Find the area of the shaded region.
3. The region R is bounded by the curve y  x 3 and

y  x 3  8x as shown in following figure.
12
b) Find the area of R.

4. Consider the region bounded by x  y2  9  0 and
2y  x  1  0 in the following figure.
a) Determine the coordinates of P and Q.

b) Find the area of the region bounded by the two functions.
5. The region R is bounded by the curve y 2  2x , y = 2 and

x = 8 as follow.
a) Find the coordinates of P and Q.

b) Find the area of region R.
6. Consider the graphs in the figure below.
a) Determine the intersection points A, B and C. 13

b) Find the area of the shaded region.

STEP 1
Sketch the bounded region
(if it is not given).
STEP 2
Look at the rotation axis
or line.
STEP 3
Use appropriate method or
given method:
VOLUME: STEP TO FIND a) Disk Method
SOLIDS OF VOLUME USING
INTEGRATION: b) Washer Method
REVOLUTION
c) Shell Method or
Cylindrical Method
STEP 4
Set up the integral using
appropriate formula/
method by finding all term
in the formula.
STEP 5
Evaluate the integral.
VOLUME BY DISKS METHOD

Disk Method 𝐴 = 𝜋𝑟 2 - full region of one curve is been
rotated
Where f(x) is the radius where f(y) is the radius

from the line of from the line of
rotation and the rotation and the
rotation is about x – rotation is about y – 14
axis or any of axis or any of vertical
horizontal line (y = k). line (x = k).

Revolves about x-axis (or line y  0)
radius  (top : curve)  (bottom : axis of rotation)

= f(x) - 0
= f(x)
VOLUME : REVOLVES ABOUT THE HORIZONTAL LINE
Revolves about line y  c

= f(x) - c
VOLUME : REVOLVES ABOUT THE HORIZONTAL LINE 15

Revolves about line y  d

 f(x)  (d)
 f(x) + d
Revolves about line y  e
radius  (top : axis of rotation)  (bottom : curve)

 e  f(x)

16

VOLUME : REVOLVES ABOUT THE VERTICAL LINE
Revolves about y-axis (or line x  0)

radius  (right : curve)  (left : axis of
rotation)
= f(y) - 0
= f(y)
Revolves about line x  a

radius  (right : curve)  (left : axis of rotation)
 f(y)  a
Volume   dy or
Volume   dy
17

Revolves about line x  b

radius  (right : curve)  (left : axis of rotation)
 f(y)  (b)
 f(y) + b
Volume   dy
Revolves about line x  e
radius  (right : axis of rotation)  (left : curve)

 e  f(y)
Volume   dy
18

EXERCISE 2
a) Find the volume of the solid that is obtained when the
region under the curve y  x over the interval [1, 4] is
revolved about the x – axis.
b) Find the volume of the solid that is obtained when the

region under the curve xy = 2 over the interval [1, 4] is
revealed about the y – axis.
19

c) Find the volume of the solid that is obtained when the area
of the region that is bounded by y  x + 2, line x  1 and
x  3 is revolved about the given axis / line.
i x-axis
ii y  1
iii y  2
iv y  7
20

d) Find the volume of the solid that is obtained when the area
of the region that is bounded by y  x , y  0 and y  2 is
revolved about the given axis / line.
i. y – axis
ii. x = -3
iii. x = 4
21

TUTORIAL
Find the volume of the solid that results when the shaded
region is revolved about the indicated axis or line.
y
1.
x  1
ans : 8 units3
2 y
.
y  x3 + x
x
1
92
ans :  units3
105
3. y
xy  2
1 22
x
ans : 3 unis3

4.
y
2x  3y
ans: 6 units3
5. y
x  y2 + 1
0 x
x3
64 2
ans:  units3
15
6. y
x1
y  4ex
ans: 8(1  e2) units3

23

PROCEDURE TO FIND THE VOLUME USING WASHER METHOD
Find inner radius
Find outer radius
Ask yourself: Axis of rotation: horizontal/vertical line?
HORIZONTAL VERTICAL
Integrate with respect to x Integrate with respect to y
Use the values on x-axis as upper and lower Use the values on y-axis as upper and lower
limit limit
Check : height  top  bottom (dx) Check : height  right  left (dy)
24

Volume by Washers • Disk Method - full

Method region of one curve is
been rotated
• where R(x) is the outer radius

from the line of rotation and r(x)
is the inner radius from the line
of rotation and the rotation is
about x – axis or any of
horizontal line (y = k).
• where R(y) is the outer radius

from the line of rotation and
r(y) is the inner radius from
the line of rotation and the
rotation is about y – axis or
any of vertical line (x = k).
25

Revolves about x-axis (or line y  0)

Outer radius  f(x)  0  [curve y  f(x)]  [axis of rotation, y  0]
 f(x)
Inner radius  g(x)  0  [curve y  g(x)]  [axis of rotation,y  0]
 g(x)
Volume 
Volume 
VOLUME : REVOLVES ABOUT THE
HORIZONTAL LINE where a  lower limit , b  upper limit and a, b located on x-axis
Revolves about line y  c

Outer radius  f(x)  c  [curve y  f(x)]  [axis of rotation, y  c]
Inner radius  g(x)  c  [curve y  g(x)]  [axis of rotation, y  c]
Volume 
Volume 
VOLUME : REVOLVES where a  lower limit , b  upper limit and a, b located on x-axis
ABOUT THE HORIZONTAL
LINE
26

Revolves about y - axis ( or line x  0)
Outer radius  f(y)  0  [curve y  f(x)]  [axis of rotation, y  0]
Inner radius  g(y)  0  [curve y  g(x)]  [axis of rotation, y  0]
Volume 
Volume 
where a  lower limit , b  upper limit and a, b located on x-axis

VOLUME : REVOLVES ABOUT
THE VERTICAL LINE
Revolves about line x  a

Outer radius  f(y)  a  [curve y  f(y)]  [axis of rotation, x  a]
Inner radius  g(y)  a  [curve y  g(y)]  [axis of rotation, x  a]
Volume 
Volume 
where a  lower limit , b  upper limit and a, b located on x-axis

VOLUME : REVOLVES ABOUT
THE VERTICAL LINE
27

EXAMPLE OF PYQ (JANUARY 2019)
Figure 3 below shows the shaded region R bounded by the curve

y  x2 and the line y = x + 2. Find the volume of the solid
generated when the shaded region R is revolved about the line
y = 5 using the Washer Method.
(5 marks)
28

EXERCISE 3
a) Find the volume of the solid generated when the shaded

region R is revolved about the line x = 1 using the Washer
Method.
29

b) Figure below show the region R which is bounded by the line

y  x  1 and the curve y  x  12. The coordinates of the
intersection between the line and the curve are (1,0) and
(2,1). Use washer Method to find the volume of the solid
generated when R is rotated about the x – axis.
30

c) The region B in Figure 2 is bounded by the curve x  y2  3,

the line 2y  x  11 and x - axis.
Figure 2
Find the volume of the solid generated when the shaded
region B is revolved about the line x = 3 using the Washer
Method.
31

d) The region W in Figure 4 is bounded by the curve y  x2,

the line x  y  6 and y - axis.
Find the volume of the solid generated by revolving the shaded

region W is revolved about x – axis using Washer Method.
32

e) Consider the shaded region R enclosed by the curves x  y

and x  2  y 2 as shown in following figure.
Find the volume of the solid by using Washer Method when the
shaded region is revolved about the line x = 2.
33

f) The shaded region is enclosed by the curve y  4  x2 and

y  2x  4.
Using Washer Method, set up the integral to find the volume

of the solid obtained when the shaded region is revolved
about the line y = 0.
34

g) Consider the shaded region R enclosed by the curves y  x2

and y 2  8x as shown as follows.
Find the volume of the solid generated by revolving R about

the x = 0 using Washer method.
35

h) Figure shows the shaded region R bounded by the parabola

Find the volume of the solid of revolution obtained by

revolving R about the y – axis using Washer method.
36

i) Figure shows the region R by the curve y  x2 , the line

Set up the integral to find the volume of the solid obtained

by revolving R about the line x = -2 using the Washer
Method. Do not evaluate the integral!
37

TUTORIAL

and x = 2.
Find the volume of the solid generated by revolving the

shaded region about the x = 1 using Washer method.

y  4x  x 2  4 .
Find the volume of the solid generated by rotating the

shaded region about the x - axis using Washer method.
38
Using Washer method, find the volume of the solid

generated when R is revolved about the x – axis.

4. Figure shows the region bounded by y  x3, y  4x and
x  0.
Find the volume of the solid obtained by rotating the

bounded region about the x - axis using the Washer method.
5. Consider the shaded region in the figure below. Set up the

integrals to find the volume of solid of revolution if the
region is revolved about the line y = -1 using the washer
method.
6. Find the volume of the solid generated by revolving the

shaded region about x-axis.
y
y + x2
yx 39
x
2

shaded region about y-axis.
(2, 4)
y  x2 y  2x

shaded region about the indicated axis or line using Washers
method.
y
a)
(1, 6)
y  9  3x
xy  6 (2, 3)
ans : 3 units3
y
b)
y  2  x2
yx
x
38
ans :  units3 40
15

y
c)
y  x2 y  4x  x2
32
ans :  units3
3
y
d)
(2, 2)
y
x
9
ans :  units3
2
y
e)
y2
yx
y  x2
x
8
ans :  units3
15
41

y
f)
y
y  x3
y  1
25
ans :  units3
21
y
g)
y  x2 +2
y  x2
x
1 5
y  1
592
ans :  units3
3
h) y
x  1
y  x2
x
1
7
ans :  units3
6 42

PROCEDURE TO FIND THE VOLUME USING SHELL METHOD
Find radius
Find height
Ask yourself: Axis of rotation: horizontal/vertical line?
HORIZONTAL VERTICAL
Integrate with respect to y Integrate with respect to x
Use the values on y-axis as upper and lower Use the values on x-axis as upper and lower
limit limit
Check : height  right - left(dy) Check : height  top - bottom(dx)
43

a) VOLUME : REVOLVES ABOUT THE VERTICAL LINE
i. Revolves about y-axis (or line x  0)

y y
y  f(x) y
f(x)
radius
heigh
x t x
a b
Radius  x (y-axis: equation of axis of rotation is x  0)

Height  top  bottom (dx)
 f(x)  0 [ top : y  f(x), bottom : y  0 (x-axis) ]
 f(x)
b
Volume  2  (radius) (height) dx
a
b
Volume  2  x  f(x) dx
a
ii. Revolves about line x  1 (bounded by one graph)

y
x1
y  f(x)
radius height
a x
b
Radius  x  1 (revolves about x  1: equation of axis of

rotation is x  1  0)

 f(x)  0 [top: y  f(x), bottom: y  0 (x-axis) ]
 f(x)
b
a
b
Volume  2  (x 1)  f(x) dx 44
a

iii. Revolves about y-axis or line x  0 (bounded by two
graphs)
y
y
y  f(x)
radiu
s height
y  g(x)
a b x
Radius  x (revolves about y-axis : equation of axis of

rotation is line x  0)
 f(x) g(x) [top: y  f(x), bottom: y  g(x) ]
b
a
b
Volume  2  x  [top  bottom] dx
a
b
Volume  2  x  [f(x)  g(x) ] dx
a
iv. Revolves about line x  1 (bounded by two graphs)

y
y
y  f(x)
radius
height
y  g(x)
a b x
x
1
Radius  x + 1 (revolves about x  1: equation of axis of
rotation is x + 1  0)
 f(x)  g(x) [ top: y  f(x), bottom: y  g(x) ]
b
a
b
Volume  2  (x + 1)  [top  bottom] dx
45
a
b
Volume  2  (x + 1)  [f(x)  g(x) ] dx
a

b) Volume : Revolves about the Horizontal Line
y
d
heigh
t x  f(y)
c
radius
Radius  y (x-axis: equation of axis of rotation is y  0)

Height  right  left (dy)
 f(y)  0 [right: x  f(y), left : x  0 (y-axis) ]
 f(y)
d
Volume  2  (radius) (height) dy
c
d
Volume  2  y  f(y) dy
c
i. Revolves about line y  2

y
d
height
x  f(y)
c radius
x
y  2
Radius  y + 2 (x-axis : equation of axis of rotation is line

y  2  y + 2  0)

 f(y)  0 [right: x  f(y), left : x  0 (y-axis) ]
 f(y)
d
46
c
d
Volume  2  (y + 1)  f(y) dy
c

ii. Revolves about x-axis (or line y  0)  bounded by two
graphs
y
x height
g(y) x
f(y)
c
radius
x
Radius  y (revolves about x-axis: equation of axis of

rotation is line y  0)
 f(y) g(y) [right: x  f(y), left : x  g(y) ]
d
c
d
Volume  2  y  [right  left] dy
c
d
Volume  2  y  [ f(y)  g(y) ] dy
c
iii. Revolves about line y  1  bounded by two graphs

y
x height
g(y) x
radius
f(y)
c y
1 x
Radius  y  1 (revolves about line y  1: equation of axis of

rotation is line y  1  0)
 f(y) g(y) [right : x  f(y), left : x  g(y) ]
d
c
d
Volume  2  (y  1)  [right  left] dy
c
47
d
Volume  2  (y  1)  [f(y)  g(y) ] dy
c

EXAMPLE OF PYQ (JANUARY 2019)
Figure 3 below shows the shaded region R bounded by the curve

y  x2 and the line y = x + 2. Find the volume of the solid
generated when the shaded region R is revolved about the line
x = -2 using the Shell Method.
(5 marks)
48

EXERCISE 4

region R is revolved about the line y = -2 using the Shell
Method.
49

b) The region W in Figure 4 is bounded by the curve y  x2,

the line x  y  6 and y - axis.
Find the volume of the solid generated when the shaded region
W is revolved about x = -1 using the Shell Method.
50

c) The region B in Figure 2 is bounded by the curve x  y2  3,

the line 2y  x  11 and x - axis.
Figure 2
Find the volume of the solid generated when the shaded
region B is revolved about the line y = -1 using the Shell
Method.
51

d) Consider the shaded region R enclosed by the curves x  y

and x  2  y 2 as shown in following figure.
Using Shell method, find the volume of the solid generated

when the shaded region is revolved about the x – axis.
52

e) The shaded region is enclosed by the curve y  4  x2 and

y  2x  4.
Find the volume of the solid by using Shell Method when the
shaded region is revolved about the line x = 2.
53

f) Consider the shaded region R enclosed by the curves y  x2

and y 2  8x as shown as follows.
Find the volume of the solid generated by revolving R about

the y = 0 using Shell method.
54

g) Figure shows the shaded region R bounded by the parabola

Find the volume of the solid of revolution obtained by

revolving R about the line y = 2 using the method of
cylindrical shells.
55

h) Figure shows the region R by the curve y  x2 , the line

Set up the integral to find the volume of the solid obtained

by revolving R about the line y = -1 using the Shell Method.
Do not evaluate the integral!
56

TUTORIAL

and x = 2.
Find the volume of the solid generated by revolving the

shaded region about the y = 0 using Shell method.

y  4x  x 2  4 .
Find the volume of the solid generated by rotating the

shaded region about the line x = 2 using the Cylindrical
Shell method.
57
Using cylindrical shells method, find the volume of the
solid generated when R is revolved about the line x = 3.

4. Figure shows the region bounded by y  x3, y  4x and
x  0.
Find the volume of the solid obtained by rotating the

bounded region about the line x = -1 using the Cylindrical
Shell method.
5. The region R is bounded by the curve y2  2x, y  2 and
x  8 as shown in figure below.
Using Shell method, find the volume of the solid generated

when region R is revolved about the line y = 5.
6. Consider the shaded region in the figure below. Set up the
integrals to find the volume of solid of revolution if the
region is revolved about the line y = -1 using the washer
method.
58

7. Use cylindrical shells to find the volume of the solid
generated when the shaded region is revolved about
e)the y-axis
f)the line x  1
y
y
x
1 4
generated when the shaded region is revolved about
a) line x  2
b) line x  1
c) line x  3
xy+20
y  x2
x
1 2

generated when the shaded region is revolved about x-axis.
y
2
y
yx
x 59
2 2

generated when the shaded region is revolved about the
indicated axis / line.
y
a)
y
x
4 128
ans :  units3
5
y
b)
y2
x
ans : 8 units3
c) y
x  2y y2
x
8
ans :  units3 60
3
d)

y
x  3  y2
x
3
9
ans :  units3
2
e)
yx
x  y2
x 
ans : unit3
6
f)
y
y  x3
(2, 8)
x  1
y  12  x2
x
8 2 61
ans :  units3
3

y
g)
y  x2
x
2
32
ans :  units3
5
y
h)
(1, 6)
y  9  3x
xy  6 (2, 3)
x
ans : 3 units3
y
i)
x  2
y  x2 + x
x
1
61
ans :  units3
15
62

j) y
x3
y  x2
y  4x  x2
32
ans :  units3
3
y
k)
y1
y  x3
x
9
ans :  units3
14
y
l)
y8
yx
2y  x + 4
x
ans : 48 units3
63

11. Figure below shows the region R bounded by the curves
y2  10  x and x  y  2 .
2

b) Determine the area of the shaded region.
c) The shaded region is rotated about the y = –2. Determine
the volume of the solid using the Shell Method.
12. Figure below shows the region R bounded by the curve

y  x  2  1 , the line y = 1 and x = 5.
a) Find the area of the region R.

b) Find the volume of the solid obtained by revolving the
region R about y = 1 by using Disk Method.
64

3. Consider the region R enclosed by the curve y = 5 – x2 and
the line = as shown in figure below.
Find the volume of the solid obtained by revolving the

region R about the line = using Washer Method.
4. The region R is bounded by the curve x = y2 + 1 and the line
y = 3 – x as shown in figure below.
Find the area of the shaded region R.

5. Consider the shaded region W enclosed by the curve y = x2 –
2x and the line y = x as shown in figure below.
65

region W is revolved about the y–axis.
b) Find the volume of the solid generated when the shaded
region W is revolved about the line y = 3.
6. The shaded region R is bounded by the curve x = y2 and the
line = as shown in figure below.
Find the area of the shaded region R.

7. The shaded region W is bounded by the curve y = x2 + 1 and
the line y = x as shown in the figure below.

region W is revolved about the y – axis by using Shell
method.
b) Find the volume of the solid generated when the shaded
region W is revolved about the line y = –1 by using
Washer method.
66

8. Find the area of the shaded region R enclosed by the curve y
= x2, the line y = 2 – x and y-axis as shown in figure
below.
9. Consider the region R, enclosed by the curve y = x3 + 1, the

line = and x-axis as shown in the figure below.
c) Use the Disk method to find the volume of the solid

obtained by revolving the region R about the x-axis.
d) Using the Shell method, set up and simplify the integral
to find the volume of the solid obtained by revolving the
region R about the line =– . Do not evaluate the
integral.
10. Figure below shows the region R bounded by the curve y =
x3, the line = and the y-axis.
a) Find the area of the region R. 67

b) By using the Washer method, find the volume generated
when the region R is rotated about the x-axis.

Chapter 5 - Applications of Integration PDF

Uploaded by

Copyright:

Available Formats

You might also like

Chapter 5 - Applications of Integration PDF

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Chapter 5 - Applications of Integration PDF

Uploaded by

Copyright:

Available Formats

MAT183 – CALCULUS I

CHAPTER 5: APPLICATIONS OF INTEGRATION

1. Sketch the graph (if graph is not given).

Evaluate the integral.

Area Between Curves (Formula Area Between Curves (Formula

• The area of • The area of

RCMN_JSM | MARCH - JULY 2019

EXAMPLE OF PYQ (JUNE 2019)

Figure 2 below shows the region R bounded by the curve

a) Find the coordinates of M and N.

RCMN_JSM | MARCH - JULY 2019

a) The region R is bounded by the curve y 2  1  x and the line

i. Find the coordinates of A and B.

RCMN_JSM | MARCH - JULY 2019

b) Figure below show the region R which is bounded by the line

RCMN_JSM | MARCH - JULY 2019

c) The region R in following figure is bounded by the curve

i. Find the coordinates of A and B.

RCMN_JSM | MARCH - JULY 2019

d) The region R in Figure 3 is bounded by the curve

i. Find the coordinates of A and B.

RCMN_JSM | MARCH - JULY 2019

e) The shaded region is bounded by the curve y  x2  x  1 and

i. Find the coordinates of A and B.

RCMN_JSM | MARCH - JULY 2019

f) The shaded region is enclosed by the curve y  4  x2 and

i. Find the coordinates of A and B.

RCMN_JSM | MARCH - JULY 2019

g) Figure shows the curves y  x2  4x  3 and y  x2  2x  3

i. Find the coordinates of A and B.

RCMN_JSM | MARCH - JULY 2019

h) Figure shows the shaded region R bounded by the parabola

i. Find the coordinates of P and Q.

RCMN_JSM | MARCH - JULY 2019

i) Figure shows the region R by the curve y  x2 , the line

i. Find the coordinates of A.

RCMN_JSM | MARCH - JULY 2019

1. Figure shows the region bounded by the curve x  1  y - 22

a) Find the coordinates of A and B.

2. Figure shows the region bounded by y  x2  4 and

Find the area of the shaded region.

3. The region R is bounded by the curve y  x 3 and

RCMN_JSM | MARCH - JULY 2019

a) Determine the coordinates of P and Q.

5. The region R is bounded by the curve y 2  2x , y = 2 and

a) Find the coordinates of P and Q.

6. Consider the graphs in the figure below.

a) Determine the intersection points A, B and C. 13

RCMN_JSM | MARCH - JULY 2019

VOLUME BY DISKS METHOD

Where f(x) is the radius where f(y) is the radius

RCMN_JSM | MARCH - JULY 2019

Revolves about x-axis (or line y  0)

radius  (top : curve)  (bottom : axis of rotation)

VOLUME : REVOLVES ABOUT THE HORIZONTAL LINE

Revolves about line y  c

VOLUME : REVOLVES ABOUT THE HORIZONTAL LINE 15