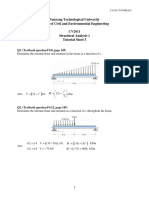
Design of Diagonal Cross Bracings

Part 1: Theoretical Study

A. PICARD and D. BEAULIEU

Diagonal bracing is commonly used in steel structures to

resist horizontal loads. In current practice, the design of
this type of bracing system is based on the assumption the
compression diagonal has negligible capacity and the ten-
sion diagonal resists the total load (Fig. 1).
If the diagonals are connected at their intersection point
(usual practice), this design procedure is conservative be-
cause the effect of this connection on the out-of-plane
buckling capacity of the compression diagonal is ig-
nored.1'2,3'4 The restraint provided to the compression di-
agonal by the loaded tension diagonal is generally sufficient
to consider that the effective length of the compression
diagonal is 0.50 times the diagonal length (KL = 0.5L) for
out-of-plane buckling as for in-plane buckling. Analytical Hypotheses:- Connections with negligible
and experimental results1'2 have also shown the ultimate moment capacity
horizontal load on the bracing system is much higher than
the horizontal component of the yielding strength of the - Diagonal in compression ignored
tension member, because of load sharing between the di-
agonals. The assumption that the compression diagonal has
negligible capacity usually results in overdesign.
This paper presents the results of a theoretical study Fig. 1. Usual design
aimed at the determination of the transverse stiffness
offered by the tension diagonal in cross-bracing systems
and at the evaluation of the effect of this stiffness on the
out-of-plane buckling resistance of the compression di-
agonal. The theory is supported by seven transverse stiff-
ness tests and 15 buckling tests. The test results are re-
ported in the second part of the paper.

BUCKLING OF THE COMPRESSION DIAGONAL

In double diagonal cross bracing, the tension diagonal acts
as an elastic spring at the point of intersection of the com-
pression diagonal as shown in Fig. 2a, where a is the spring
stiffness (kips/in. or kN/mm). If a = 0, then K = 1.0 (Fig.
2b) and the elastic critical load Cce is equal to:

A. Picard is Professor of Civil Engineering, Laval University,

Quebec, Canada.
D. Beau lieu is Associate Professor of Civil Engineering, Laval
University.
Fig. 2. Buckling modes for compression diagonal

122 ENGINEERING JOURNAL / AMERICAN INSTITUTE OF STEEL CONSTRUCTION

 In this equation, Ic is the moment of inertia of the com- The variation of the dimensionless elastic buckling load is
pression diagonal considering out-of-plane buckling. shown in Fig. 3 in terms of the dimensionless spring stiff-
If a = °°, then K = 0.5 and the elastic critical load is ness. The exact solution obtained by Timoshenko and Gere
equal to: is also shown in the figure. It can be seen that Eq. 7 is
slightly conservative.
4TT2EIC
r = 4C„ (2) Using Eqs. 3 and 7, the effective length factor becomes:

Therefore, the effective length factor is given by: K= 0.5 (8)

V l 6 + 37

K= \ l ^ (3) The variation of K is plotted in Fig. 4 against the dimension-

r less spring stiffness. The exact solution, given in Refs. 5 and
Timoshenko and Gere 5 demonstrated there is a limit 6, is also shown in the figure.
spring stiffness above which the elastic critical load is 4Ce
TRANSVERSE STIFFNESS OF
(Fig. 2c). In other words, the spring does not have to be
THE TENSION DIAGONAL
infinitely stiff to obtain K = 0.5. The limit spring stiffness is
given by:5 To determine the parameters a and 7, we will consider a
prismatic member subjected to a transversely applied point
aiim = 7T^ (4) load Q and a concentrically applied tensile force T, as
Lr shown in Fig. 5. For the problem studied here, Q represents
Let us define the non-dimensional spring stiffness as: the transverse force transmitted to the tension diagonal by
the compression diagonal at buckling.
= oL The general solution of the differential equation ob-
7 (5)
" C tained from equilibrium of the tension member shown in
Fig. 5 is classical, assuming elastic behavior. The elastic
From Eqs. 1, 4 and 5, the limit value of the non- behavior assumption is easily satisfied for X-bracing, since
dimensional spring stiffness is equal to: both diagonals are identical. When the compression di-
agonal buckles, the tension diagonal is still behaving
7lim = CXlim — = 1 6
(6) elastically.1'2
The transverse stiffness or spring stiffness provided by
If we assume a linear relationship between Cce and 7, we the tension diagonal is obtained from the solution of the
obtain: differential equation and is given by:1'2

Cr„ = | l + — I C < \CP (7) a=m\ 3

\ L ) (v - tank v)
(9)

fS
4>
Exact solution (Ref. 5 ) - \

- s i n u + 4 u cos u ( 7 - — " F j ^
v ^
where i
Cce 2VEI C ,1/
Ce 1 ' //
\ 'J/

Jnear re ation (Eq . 7 )

//
S/S
SS
4/
AS

\y\ 8 10 12 14 16 18 20
Y

Fig. 3. Relationship between elastic buckling load and non- Fig. 4. Relationship between effective length factor and non-
dimensional spring stiffness dimensional spring stiffness

THIRD QUARTER/1987 123

where v is defined as: The following approximation for Eq. 12 is proposed:

Hfr EI,
(10) 7 = ^ - ( 3 + 1.09v2) (13)

In Eqs. 9 and 10, E is the elastic modulus of the material Eqs. 12 and 13 are compared in Fig. 6. It can be seen Eq. 13
and It is the moment of inertia of the tension diagonal, very closely approximates Eq. 12 when 0 < v 2 < 80. This
considering out-of-plane bending of the X-bracing. practical range for parameter v 2 was evaluated as follows.
Combining 1, 5 and 9, we obtain the following equation Let us first assume the out-of-plane slenderness ratio of
for the evaluation of the dimensionless spring stiffness: the compression diagonal, i.e., both diagonals, should not
exceed 200. Since the diagonals are connected at their
(11) intersection, we get:
\ i r 2 / \ / c / ( v - tank v)
L/2
In X-bracing systems, both diagonals are identical and It = 200
r
Ic = I. However, in X-trusses supporting loads which al-
ways act in the same direction, the compression diagonal LY
40 0 0 0 - (14)
could be stiffer. Since this paper deals with double diagonal 2, A
bracings, Eq. 11 can be rewritten as:
The maximum force in the tension diagonal being AFy, Eq.
7 = (12) 10 together with Eq. 14 and E = 29 000 ksi leads to:
TT / (v - tank v)
l\AFy
'A EI
T
Considering a maximum value for Fy of 58 ksi, then 0 < v 2
— —'— ffflfffo
< 80.
In the previous equation, the constant 1.38 is in (ksi) -1 . If
0.5 L -0.5 L- SI units are used E - 200 000 MPa and the constant is equal
Fig. 5. Tension member subjected to transverse force at mid-span to 0.20 (MPa)~\ Then Fy is in MPa.

160
ss\
140

120
f

100
$7
80
Exact solution (Eq.l2K

V
4 4y
^ - L i n * ar relatio n (Eq. 13

60

4
40
AS
AS
/y
20

1^4.86
10 20 3 0 4 0 5 0 6 0 7 0 8 0 9 0

Fig. 6. Comparison of Eqs. 12 and 13

124 ENGINEERING JOURNAL / AMERICAN INSTITUTE OF STEEL CONSTRUCTION

 Eq. 13, being an acceptable approximation (Fig. 6), will tions was ignored. In Ref. 4, the rotational restraint was
be used in the theoretical analysis. Since Ic = It = /, relatively important, and test results suggest use of an
combining Eqs. 1, 5, 10 and 13 gives: effective length factor of 0.85 times the half diagonal
length, i.e., K = 0.425 if the total length of the diagonal is
a = Q , = 48|/ + 4 3 6 r considered.
E L 3 L
It is interesting to note the first term in Eq. 15 represents the COMPRESSION-TENSION RATIO
flexural stiffness of the tension diagonal. Then T = 0, the
spring stiffness is equal to the flexural stiffness. Therefore a Since the behavior of the braced frame shown in Fig. 1 is
is never equal to zero and K is always smaller than 1.0 (a min elastic up to buckling of the compression diagonal, the ratio
= 48 EIIL3; from Eq. 5 or Eq. 18,7 min = 4.86; from Eq. 8, CceIT is equal to the ratio of the force in the compression
Kmax = 0.72 (see Fig. 4). diagonal C to that in the tension diagonal T obtained from
The results of the transverse stiffness tests reported in the an elastic analysis of the frame. Eq. 19 can thus be rewritten
second part of the paper demonstrate the validity of Eqs. 13 as:
and 15.
Eq. 10 can be rewritten as: K= \/0.523-^Uo.50 (20)
CIT
TTL\2 T
= 2.47- (16) Eq. 20 is plotted in Fig. 7. As seen, when the CIT ratio is
2 J T:2EI Ce larger than 1.6, the effective length factor increases. It
Introducing Eq. 16 into Eq. 13 gives: reaches its maximum value when the CI T ratio is equal to

y = 4.86 + 4.36 — (17) 0.75,

1
r ~~'
KMQ,
t = 0.72 • !
From Eq. 3, Ce = K2CC( Therefore, Eq. 17 can be 0.70
rewritten as:

y = 4.86 + 4.36 (18) 0.65

K2Cr, ^ - ( E q . J iO)

Combining 8 and 18 gives: 0.60

K= \/0.523--^->0.50 (19) 0.55

CrJT
= 1.6
During the buckling tests reported in the second part of
the paper, the force in the tension diagonal was kept con-
0.50. L vC.,.
2 4
|J
6 8 10 12 14
stant. Therefore, the value of T is known. If the compres- C/T
sion diagonal buckles in the elastic range, Eq. 19 can be Fig. 7. Effective length factor vs. CIT ratio
used to determine the effective length factor (Cce = Ccr
where Ccr is the measured buckling load). For inelastic 2.0
buckling, Eq. 19 is not valid. However, the measured ine-
lastic buckling load can be introduced into AISC equations7
y
(safety factor removed) or into CSA equations8 (resistance 1.8
factor removed) to determine the effective length factor.
With this value of K, two values of Cce can be computed.
One is obtained from Eq. 19 and the other from the follow-
ing equation: Cce = TT2 EII(KE)2. These two values are C/T
1.6
rT 5
K = 0.3-7)
n•° ^•^•^i

compared to evaluate the accuracy of Eq. 19. 1.4 1 (see fi

Two final comments should be made concerning the
previous equations. These equations are valid for con- _60^_
tinuous diagonals which are connected at their intersection 1.2
point. If one diagonal is interrupted at the intersection
point, constant stiffness is not maintained and the connec-
tion at this point may become a weak link when the inter- IQ r^\ 0.4
0.2
1
0.6 0.8 1.0 1.2 1.4 \J
rupted diagonal is compressed.3 A/A b
In the derivations the rotational restraint of the connec- Fig. 8. Variation in CIT ratio with AIAb ratio (Eq. 22)

THIRD QUARTER/1987 125

infinity, which corresponds to the minimum spring stiff-
ness, equal to the flexural stiffness of the tension diagonal
(T = 0 in Eq. 15 or Eq. 17).
By considering the elastic deformations of the braced
frame shown in Fig. 1, Vickers3 derived the following equa-
tion to compute the CIT ratio:
C = 1 + cos3^
T
^ i + Asin36
A \ Ac J ful to Moffet and to the Natural Sciences and Engineering
The parameters of this equation are defined in Fig. 1. Eq.
21 was derived for a load pushing against one side of the
frame as in Fig. 1. This is the most critical loading condition
for the design of the compression diagonal because the CIT
ratio exceeds one. 3
In a typical braced frame, the area of the cross section of
the columns Ac is usually much greater than the area of the
cross section of the diagonals A. Moreover, sin39 is always
smaller than one. Consequently, the term A sin39A4cinEq.
21 is small compared to 1 and can be neglected with only a
minor loss in accuracy resulting in errors which are on the
conservative side. Eq. 21 becomes:
f.1 + (A) cos > e m
Eq. 22 is plotted in Fig. 8. It can be seen that large values of
Ab, i.e. small values of the AIAb ratio, tend to equalize the
forces in the diagonals. In practical situations, the AIAb
ratio is much smaller than one. Therefore, as shown in Fig.
8, the CIT ratio is usually smaller than 1.6 and the l v a l u e is
equal to 0.5 (Fig. 7).
CONCLUSION
The theoretical study reported in this paper shows that in
double diagonal bracing systems the effective length of the
compression diagonal is 0.5 times the diagonal length when
the diagonals are continuous and attached at the intersec-
tion point.
Tests were done to demonstrate the validity of the equa-
tions used to determine the transverse stiffness or spring
126 ENGINEERING JOURNAL / AMERICAN INSTITUTE OF STEEL CONSTRUCTION
stiffness provided by the tension diagonal and the validity
of the equations used to determine the effective length
factor. The results of these tests are reported in the second
part of the paper.
ACKNOWLEDGMENTS
A part of the results presented in the paper are drawn from
the Master's thesis of Pierre Moffet. The writers are thank-
Research Council of Canada for its financial support.
REFERENCES
1. DeWolf, J. T. and J. F. Pellicione Cross-Bracing De-
sign ASCE Journal of the Structural Division, Vol.
105, ST7, July 1979 (pp. 1,379-1,391).
2. Kitipornchai, S. and D. L. Finch Double Diagonal
Cross Bracings in Buildings Research Report No.
CE56, Department of Civil Engineering, University of
Queensland, Australia, November 1984.
3. Vickers, D. G. Tension-Compression Cross Bracing
Using Star Angles Mechanical Engineering Project Re-
port, Department of Civil Engineering, McGill Universi-
ty, May 1982, Montreal.
4. El-Tayem, A. A. and S. C. Goel Effective Length
Factor for the Design of X-bracing Systems AISC En-
gineering Journal, IstQtr., 1986, Chicago, III. (pp. 41-
45).
5. Timoshenko, S. P. and J. M. Gere Theory of Elastic
Stability McGraw-Hill Book Co., 1961, New York,
N.Y. (pp. 70-73).
6. Moffet, P. and D. Beaulieu Resistance au flambement
de pieces comprimees supportees en divers points par
des pieces tendues Report GCT-06-03 (in French), De-
partment of Civil Engineering, Laval University, April
1986.
1. American Institute of Steel Construction, Inc. Specifi-
cation for the Design, Fabrication and Erection of
Structural Steel for Buildings 1978, Chicago, III.
8. Canadian Standards Association Steel Structures for
Buildings—Limit States Design Standard CAN3-
S16.1, 1984, Rexdale, Ontario.