Professional Documents
Culture Documents
Facts at Your Fingertips-200410-Fluid Mechanics
Facts at Your Fingertips-200410-Fluid Mechanics
Uploaded by
onizuka-t2263Copyright:
Available Formats
You might also like
- Solution Manual for an Introduction to Equilibrium ThermodynamicsFrom EverandSolution Manual for an Introduction to Equilibrium ThermodynamicsNo ratings yet
- Cooling Tower SOPDocument8 pagesCooling Tower SOPBoiler Scrubber50% (2)
- WPS, PQR and WPQDocument31 pagesWPS, PQR and WPQDhrumil Chauhan100% (2)
- Fluid Flowrev01Document4 pagesFluid Flowrev01Christian Mercado PagsinohinNo ratings yet
- PumpDocument13 pagesPumpHarshal ButleNo ratings yet
- 3.1 Cryogenic Fluid Mechanics: Fluid Flow Commonly Occurs in Most Cryogenic SystemsDocument28 pages3.1 Cryogenic Fluid Mechanics: Fluid Flow Commonly Occurs in Most Cryogenic SystemsAbd NaamiNo ratings yet
- PVDH GDH: Chapter SeventeenDocument1 pagePVDH GDH: Chapter SeventeenEaswaran NampoothiriNo ratings yet
- Ognition PSV Sizing Calculation SpreadsheetDocument2 pagesOgnition PSV Sizing Calculation SpreadsheetJoseph Paul IlaganNo ratings yet
- Hazen William's Equation: by Eng. Ahmed Ghassan & Eng. Ahmed AmmarDocument13 pagesHazen William's Equation: by Eng. Ahmed Ghassan & Eng. Ahmed AmmarvasudhaNo ratings yet
- Pipeline Virtual Anchor Length Calculations: VariablesDocument3 pagesPipeline Virtual Anchor Length Calculations: Variablesromvos8469No ratings yet
- Length of ReactorDocument5 pagesLength of ReactorLily Antonette AgustinNo ratings yet
- JavaProp Users GuideDocument69 pagesJavaProp Users GuideNurhayyan Halim RosidNo ratings yet
- Similarity Between Convective Heat Transfer and Convective Mass TransferDocument9 pagesSimilarity Between Convective Heat Transfer and Convective Mass TransferHanif IndraNo ratings yet
- Appendix C - Calculation of Face BoltDocument20 pagesAppendix C - Calculation of Face BoltDEBASIS BARMAN100% (1)
- Conférence AvellanF PDFDocument34 pagesConférence AvellanF PDFceice2013No ratings yet
- Ognition PSV Sizing Calculation SpreadsheetDocument2 pagesOgnition PSV Sizing Calculation Spreadsheetrisqi ilham zulfahmiNo ratings yet
- Hydroelectric System Models: 3.1 Preliminary ConceptsDocument51 pagesHydroelectric System Models: 3.1 Preliminary ConceptsTilahun weldcherkosNo ratings yet
- Bottom Hole PressureDocument30 pagesBottom Hole PressuredinoNo ratings yet
- Gasdynamics AE4140 Chapter 1: IntroductionDocument60 pagesGasdynamics AE4140 Chapter 1: IntroductionPythonraptorNo ratings yet
- Refrigeration & Air Conditioning (MPE411) - Lec.2 - 2Document70 pagesRefrigeration & Air Conditioning (MPE411) - Lec.2 - 2Bassem OstoraNo ratings yet
- Section 12Document49 pagesSection 12Asad KhanNo ratings yet
- Hydropower Engineering: Turbines. Basic ConceptsDocument22 pagesHydropower Engineering: Turbines. Basic ConceptsHenrry RojasNo ratings yet
- Turbomachinery For Compressible FluidsDocument70 pagesTurbomachinery For Compressible FluidsArun BeniwalNo ratings yet
- Sistemas de Producción 11 - Curva de SalidaDocument59 pagesSistemas de Producción 11 - Curva de SalidaLuis Vallejo EstrellaNo ratings yet
- HVACR Formulas and SymbolsDocument46 pagesHVACR Formulas and SymbolsatiqNo ratings yet
- Mega Part2 cb1Document101 pagesMega Part2 cb1romy94496No ratings yet
- Civil Engineering FormulasDocument6 pagesCivil Engineering FormulasJonathan100% (3)
- Reciprocating+Compressors+ +3.+Useful+CorrelationsDocument17 pagesReciprocating+Compressors+ +3.+Useful+CorrelationsChristopherNo ratings yet
- Solved Problems in Soil Mechanics: SolutionDocument10 pagesSolved Problems in Soil Mechanics: SolutionMemo Ly100% (1)
- Lecture 26Document8 pagesLecture 2606me395No ratings yet
- Fundamentals of Compressible Flows in Pipelines: Dr. Ahmed Elmekawy Fall 2018Document74 pagesFundamentals of Compressible Flows in Pipelines: Dr. Ahmed Elmekawy Fall 2018Tamunoiboumie ElijahNo ratings yet
- ConvectionDocument26 pagesConvectionDozdiNo ratings yet
- Feuille Exercices Electrotechnique TDDocument3 pagesFeuille Exercices Electrotechnique TDanass sbniNo ratings yet
- 2.065/2.066 Acoustics and Sensing: Massachusetts Institute of TechnologyDocument12 pages2.065/2.066 Acoustics and Sensing: Massachusetts Institute of TechnologyKurran SinghNo ratings yet
- Part 10Document8 pagesPart 10Kerlos SaeedNo ratings yet
- Analysis of Compressible Flow in FUNDAMENTALS OF FLUID MECHANICSDocument210 pagesAnalysis of Compressible Flow in FUNDAMENTALS OF FLUID MECHANICSAjay kumar100% (1)
- Fundamentals of Fluid Mechanics Chapter 11 Analysis of Compressible FlowDocument210 pagesFundamentals of Fluid Mechanics Chapter 11 Analysis of Compressible FlowJake OkuyeNo ratings yet
- Topic 7 - Flow of Compressible FluidsDocument85 pagesTopic 7 - Flow of Compressible Fluidszairulh7No ratings yet
- Appendix C C. Formulae A. Chapter 1 Relations: E 2 - 14 3 2 2 2 E 24 E 6 2 C M 2 F Avog 26 26Document17 pagesAppendix C C. Formulae A. Chapter 1 Relations: E 2 - 14 3 2 2 2 E 24 E 6 2 C M 2 F Avog 26 26Ivelin ValchevNo ratings yet
- Surgetrol Tank SizingDocument1 pageSurgetrol Tank SizingAnonymous WpFsSj9sy1No ratings yet
- ME 4061 Compressible FlowDocument18 pagesME 4061 Compressible FlowFatih İnalNo ratings yet
- Crack Evaluation and Mitigation - CalculationDocument4 pagesCrack Evaluation and Mitigation - CalculationSilvioNo ratings yet
- Compressible Flow PDFDocument210 pagesCompressible Flow PDFRicky JuwonoNo ratings yet
- Rumus Head Loss BernoulliDocument2 pagesRumus Head Loss BernoulliZmique AzmiNo ratings yet
- Free Convection-9a PDFDocument16 pagesFree Convection-9a PDFSaeed AbdNo ratings yet
- Rigid conduit for fluid flow in two-phase fluid systems - MATLAB - MathWorks 中国Document6 pagesRigid conduit for fluid flow in two-phase fluid systems - MATLAB - MathWorks 中国944062528qqNo ratings yet
- PDF P324 06A (For Class) Lec Mod2 04a Diffusivity Eq (Orientation) PDFDocument18 pagesPDF P324 06A (For Class) Lec Mod2 04a Diffusivity Eq (Orientation) PDFvitaxnNo ratings yet
- Sample FormulasDocument6 pagesSample FormulasAhmedNo ratings yet
- 2900 - 4. FMEC Nozzle Theory PDFDocument46 pages2900 - 4. FMEC Nozzle Theory PDFMohmmmad HussainNo ratings yet
- Phys101 Term:121 Online HW-Ch14-Lec01Document2 pagesPhys101 Term:121 Online HW-Ch14-Lec01Amarjeet kaurNo ratings yet
- Assessment of Single-And Two-Zone Modeling of Centrifugal Compressors Studies in Component Performance: Part 3Document13 pagesAssessment of Single-And Two-Zone Modeling of Centrifugal Compressors Studies in Component Performance: Part 3khknimaNo ratings yet
- Calculation FD Fan PowerDocument7 pagesCalculation FD Fan PowerIrwansyah MuchtarNo ratings yet
- Analysis and Design of Transport Equipment: Anwar Ilmar Ramadhan, S.ST, MTDocument33 pagesAnalysis and Design of Transport Equipment: Anwar Ilmar Ramadhan, S.ST, MTEva AmeliaNo ratings yet
- Basic Drilling Engineering EquationsDocument6 pagesBasic Drilling Engineering EquationsFarah Omar FarahNo ratings yet
- Internal Flow: Heat Transfer CorrelationsDocument9 pagesInternal Flow: Heat Transfer CorrelationsbaroNo ratings yet
- SMD 1 2020 Z SNF HS CAL 0001 02 Safety Relief Valve Load Calculations (AutoRecovered)Document4 pagesSMD 1 2020 Z SNF HS CAL 0001 02 Safety Relief Valve Load Calculations (AutoRecovered)Amr TarekNo ratings yet
- Uniform Flow in Open Channels Economical SectionsDocument16 pagesUniform Flow in Open Channels Economical Sectionscarl ingariNo ratings yet
- Gas RateDocument2 pagesGas RateArif KhanNo ratings yet
- Engineering Calculation: (This Correlated Heat Transfer Coefficient at Tube Side Condition of Flow)Document3 pagesEngineering Calculation: (This Correlated Heat Transfer Coefficient at Tube Side Condition of Flow)RajdeepsinhNo ratings yet
- Kaplan Turbines SlidesDocument28 pagesKaplan Turbines Slidesjonas61700700100% (2)
- The Spectral Theory of Toeplitz Operators. (AM-99), Volume 99From EverandThe Spectral Theory of Toeplitz Operators. (AM-99), Volume 99No ratings yet
- Facts at Your Fingertips-201104-Hopper Inserts For Improved Solids FlowDocument1 pageFacts at Your Fingertips-201104-Hopper Inserts For Improved Solids Flowonizuka-t2263No ratings yet
- Facts at Your Fingertips-201105-Pressure Measurement ConsiderationsDocument1 pageFacts at Your Fingertips-201105-Pressure Measurement Considerationsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201101-Hansen Solubility Parameters (HSP)Document1 pageFacts at Your Fingertips-201101-Hansen Solubility Parameters (HSP)onizuka-t2263No ratings yet
- Facts at Your Fingertips-201007-Conservation Economics Carbon Pricing ImpactsDocument1 pageFacts at Your Fingertips-201007-Conservation Economics Carbon Pricing Impactsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201102-Control Valve Position SensorsDocument1 pageFacts at Your Fingertips-201102-Control Valve Position Sensorsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201010-MSMPR Crystallization EquipmentDocument1 pageFacts at Your Fingertips-201010-MSMPR Crystallization Equipmentonizuka-t2263No ratings yet
- Facts at Your Fingertips-201103-Infrared Temperature MeasurementDocument1 pageFacts at Your Fingertips-201103-Infrared Temperature Measurementonizuka-t2263No ratings yet
- Facts at Your Fingertips-201009-Controlling Membrane FoulingDocument1 pageFacts at Your Fingertips-201009-Controlling Membrane Foulingonizuka-t2263No ratings yet
- Facts at Your Fingertips-201011-Viscosity MeasurementDocument1 pageFacts at Your Fingertips-201011-Viscosity Measurementonizuka-t2263No ratings yet
- Facts at Your Fingertips-201005-Burner Operating Characteristics PDFDocument1 pageFacts at Your Fingertips-201005-Burner Operating Characteristics PDFonizuka-t2263No ratings yet
- Facts at Your Fingertips-201008-Heat Transfer Fluids System FiltrationDocument1 pageFacts at Your Fingertips-201008-Heat Transfer Fluids System Filtrationonizuka-t2263No ratings yet
- Facts at Your Fingertips-201012-Project Design Decision-Making Option ListsDocument1 pageFacts at Your Fingertips-201012-Project Design Decision-Making Option Listsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201003-Steam Tracer Lines and Traps PDFDocument1 pageFacts at Your Fingertips-201003-Steam Tracer Lines and Traps PDFonizuka-t2263No ratings yet
- Facts at Your Fingertips-200810-Heat TransferDocument1 pageFacts at Your Fingertips-200810-Heat Transferonizuka-t2263No ratings yet
- CHE Facts 0410Document1 pageCHE Facts 0410gwinnruNo ratings yet
- Facts at Your Fingertips-201002-Positive Displacement PumpsDocument1 pageFacts at Your Fingertips-201002-Positive Displacement Pumpsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201005-Burner Operating Characteristics PDFDocument1 pageFacts at Your Fingertips-201005-Burner Operating Characteristics PDFonizuka-t2263No ratings yet
- Facts at Your Fingertips-200811-Alternative Fuels (Bio Diesel)Document1 pageFacts at Your Fingertips-200811-Alternative Fuels (Bio Diesel)onizuka-t2263No ratings yet
- Facts at Your Fingertips-200907-Flowmeter SelectionDocument2 pagesFacts at Your Fingertips-200907-Flowmeter Selectiononizuka-t2263No ratings yet
- Facts at Your Fingertips-200812-Fluid FlowDocument1 pageFacts at Your Fingertips-200812-Fluid Flowonizuka-t2263No ratings yet
- Facts at Your Fingertips-200809-CrystallizationDocument1 pageFacts at Your Fingertips-200809-Crystallizationonizuka-t2263No ratings yet
- Summary: Ionic EquilibriaDocument33 pagesSummary: Ionic Equilibriawewwchemistry100% (1)
- I V Savelyev Physics General Course Vol 3Document319 pagesI V Savelyev Physics General Course Vol 3thuongtunhienNo ratings yet
- Evaluation of Seismic Ground MotionDocument24 pagesEvaluation of Seismic Ground MotionmillzNo ratings yet
- Assignment No. 1Document9 pagesAssignment No. 1Cheryl Lou SantiagoNo ratings yet
- Stiffening Ring Cal For Exteneral Press.Document11 pagesStiffening Ring Cal For Exteneral Press.inspectormhp100% (1)
- Petrucci 11e PPT Ch07Document62 pagesPetrucci 11e PPT Ch07JOHN ZEDWIN STA. MONICANo ratings yet
- User Guide Sika Carbodur TR55Eurocode2 EnglishDocument52 pagesUser Guide Sika Carbodur TR55Eurocode2 EnglishMihaiNo ratings yet
- Polymer ProcessingDocument28 pagesPolymer ProcessingMousom SomNo ratings yet
- CH 16 Slides MDocument98 pagesCH 16 Slides MJennifer L. MadronioNo ratings yet
- Development of Processes For C4 Hydrocarbons SeparationDocument11 pagesDevelopment of Processes For C4 Hydrocarbons SeparationTasneem MNo ratings yet
- XII-NEET: 2021-22: Solutions Chemical EquilibriumDocument2 pagesXII-NEET: 2021-22: Solutions Chemical EquilibriumLalit KNo ratings yet
- Heat TreatmentDocument6 pagesHeat TreatmentjotikaNo ratings yet
- Temperature, Heat and The First Law of ThermodynamicsDocument3 pagesTemperature, Heat and The First Law of ThermodynamicspedroNo ratings yet
- GENCHM280 SolutionDocument58 pagesGENCHM280 SolutionReysel MonteroNo ratings yet
- Muthu Cad 2Document8 pagesMuthu Cad 2Sagarias AlbusNo ratings yet
- A Presentation ON Prototype: Dimensional Accuracy: Dr. D.Y PATIL College of Engineering Akurdi, Pune Maharashtra - 411044Document10 pagesA Presentation ON Prototype: Dimensional Accuracy: Dr. D.Y PATIL College of Engineering Akurdi, Pune Maharashtra - 411044AkshayJadhavNo ratings yet
- Total MixerDocument2 pagesTotal MixerFeroz KhanNo ratings yet
- Ultrasonics Sonochemistry: Bogdan NiemczewskiDocument6 pagesUltrasonics Sonochemistry: Bogdan NiemczewskiOmid7686No ratings yet
- Design of Plate Girder MCQDocument2 pagesDesign of Plate Girder MCQAvinash Kumar (RA1911001030001)No ratings yet
- Vibration IsolationDocument8 pagesVibration Isolationofitecnicajg100% (1)
- Investigatory Project Physics by RonitDocument17 pagesInvestigatory Project Physics by RonitronitsuniyaNo ratings yet
- Bafer 100.VE.06 PDFDocument61 pagesBafer 100.VE.06 PDFVasiljka Đordan JelacaNo ratings yet
- Cambridge IGCSE: Physics 0625/23Document20 pagesCambridge IGCSE: Physics 0625/23Manya PunjabiNo ratings yet
- Formulation and Evaluation of Microemulsion Based Gel of KetoconazoleDocument19 pagesFormulation and Evaluation of Microemulsion Based Gel of KetoconazoleAndre HopfnerNo ratings yet
- Transformation of Electrical EnergyDocument8 pagesTransformation of Electrical EnergyAnaluz Redondo GoleñaNo ratings yet
- 5a - PumpTraining 032306Document32 pages5a - PumpTraining 032306Islam SolimanNo ratings yet
- LN - 10 - 51 - E-Learning Hydrological CycleDocument8 pagesLN - 10 - 51 - E-Learning Hydrological CycleMaria OzaoNo ratings yet
- Chapter 16 Radiation Protection and Safety PDFDocument236 pagesChapter 16 Radiation Protection and Safety PDFAshutosh SinghNo ratings yet
Facts at Your Fingertips-200410-Fluid Mechanics
Facts at Your Fingertips-200410-Fluid Mechanics
Uploaded by
onizuka-t2263Original Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Facts at Your Fingertips-200410-Fluid Mechanics
Facts at Your Fingertips-200410-Fluid Mechanics
Uploaded by
onizuka-t2263Copyright:
Available Formats
FLUID MECHANICS
FACTS AT YOUR FINGERTIPS
ENERGY RELATIONSHIPS PUMP, COMPRESSOR PUMP, COMPRESSOR AND
(Incompressible flow) AND PIPE EQUATIONS PIPE EQUATIONS (Continued)
Bernoulli’s equation Economic pipe diameter Suction specific speed (S)
1/ 6
) (1/ ρ2 ) ⎤⎥
1/ 2
⎡10 ⋅ PC ⋅ m˙ 3f 4 / π
( S = N ⋅ Q 3/ 4
2
D econ = ⎢⎢ ⎥
(NPSH )
CC ⋅ PP
Diffusers and sudden expansions: ⎢⎣ ⎥⎦
Specific diameter (Ds)
Pump power output (Q at full capacity) (Compressors)
0.25
Friction heating in a pipe D s = D ⋅ H0.5
kW = H ⋅ Q ⋅ ρ / 3.670 × 10 5 Q
(Laminar flow of Newtonian fluids)
(H in N·m/kg; Q in m3/h; ρ in kg/m3)
Flow coefficient (φ)
kW = H ⋅ Q / 3.599 × 10 6 (Compressors)
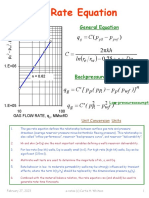
Torricelli’s equation (H in Pa; Q in m3/h)
φ= Q
(For flow from the bottom of a vessel) 3
N ⋅D3
hp = H ⋅ Q ⋅ s / 3.960 × 10
V2 = 2 ⋅ g ⋅ h (H in lbf·ft/lbm; Q in gal/min) Pressure coefficient (ψ)
(Compressors)
Pressure-depth relationship hp = H ⋅ Q / 1.714 × 10 3 ψ = H
(Constant density) (H in lbf /in.2; Q in gal/min) N 2 ⋅ D2
(
P2 − P1 = − ρ ⋅ g z 2 − z 1 ) Net positive suction head* Nomenclature
(Be sure to convert pressure units to head)
atm atmospheric pressure
Reynolds number (NPSH)A = hss – hfs – p A area
D ⋅V ⋅ ρ BHP brake horsepower, hp
Re = For an existing installation:
c speed of sound
µ (NPSH)A = atm + hgs – p + hvs CC capital charge constant, 1/yr
Friction factor (f ) *To avoid cavitation, (NPSH)A ≥ (NPSH)R D diameter
D0 diameter at the pipe wall
1 = −4 log⎡ 0.27 ε + 7 / Re 0.9 ⎤
f ⎢⎣ D ( ) ⎥⎦ Head-flow relationship (pumps) f friction factor
friction heating per unit mass
Re > 4,000 (Q2 )2 = h2 g gravity constant
(Q1)2 h1
h head
Mach number hfs suction friction head
hgs gage reading at the suction flange
M = V/c Specific speed (Ns)** of a pump
0.5 hss static suction head
Speed of sound N s = N ⋅ 0Q.75 hvs velocity head at point of gage
H attachment
⎛ ⎞
c = ⎜K ⎟ (Q in gal/min; H in ft·lbf /lbm) H total dynamic head
⎝ ρ⎠ K
•
bulk modulus
**For compressors, H is adiabatic head m mass flowrate
M Mach number
(NPSH)A available net positive suction head
The Affinity Laws (pumps) (NPSH)R required net positive suction head
N impeller rotational speed, rpm
Constant impeller dia. Constant impeller speed p vapor pressure
(D = impeller dia.) P pressure
PC pumping cost constant, $/(hp·yr)
Capacity Q1 N1 Q1 D1
= = PP purchase price constant,
Q2 N 2 Q 2 D2 $/[in. (dia.) · ft (of length)]
Q volumetric flowrate
Head H1
=
( )
N1
2
h1
=
( )
D1
2 Re
s
Reynolds number
specific gravity
H2 N2 ( )2 h2 D2( )2 V
z
velocity
position in the direction opposite
that of gravity
Break BHP1
=
N1( )3 BHP1
=
P1 ( )3 ε pipe roughness
horsepower µ
BHP2 N2( )3 BHP2 P2 ( )3 ρ
fluid viscosity
density
FACTS AT YOUR FINGERTIPS IS SPONSORED BY:
TLFeBOOK
You might also like
- Solution Manual for an Introduction to Equilibrium ThermodynamicsFrom EverandSolution Manual for an Introduction to Equilibrium ThermodynamicsNo ratings yet
- Cooling Tower SOPDocument8 pagesCooling Tower SOPBoiler Scrubber50% (2)
- WPS, PQR and WPQDocument31 pagesWPS, PQR and WPQDhrumil Chauhan100% (2)
- Fluid Flowrev01Document4 pagesFluid Flowrev01Christian Mercado PagsinohinNo ratings yet
- PumpDocument13 pagesPumpHarshal ButleNo ratings yet
- 3.1 Cryogenic Fluid Mechanics: Fluid Flow Commonly Occurs in Most Cryogenic SystemsDocument28 pages3.1 Cryogenic Fluid Mechanics: Fluid Flow Commonly Occurs in Most Cryogenic SystemsAbd NaamiNo ratings yet
- PVDH GDH: Chapter SeventeenDocument1 pagePVDH GDH: Chapter SeventeenEaswaran NampoothiriNo ratings yet
- Ognition PSV Sizing Calculation SpreadsheetDocument2 pagesOgnition PSV Sizing Calculation SpreadsheetJoseph Paul IlaganNo ratings yet
- Hazen William's Equation: by Eng. Ahmed Ghassan & Eng. Ahmed AmmarDocument13 pagesHazen William's Equation: by Eng. Ahmed Ghassan & Eng. Ahmed AmmarvasudhaNo ratings yet
- Pipeline Virtual Anchor Length Calculations: VariablesDocument3 pagesPipeline Virtual Anchor Length Calculations: Variablesromvos8469No ratings yet
- Length of ReactorDocument5 pagesLength of ReactorLily Antonette AgustinNo ratings yet
- JavaProp Users GuideDocument69 pagesJavaProp Users GuideNurhayyan Halim RosidNo ratings yet
- Similarity Between Convective Heat Transfer and Convective Mass TransferDocument9 pagesSimilarity Between Convective Heat Transfer and Convective Mass TransferHanif IndraNo ratings yet
- Appendix C - Calculation of Face BoltDocument20 pagesAppendix C - Calculation of Face BoltDEBASIS BARMAN100% (1)
- Conférence AvellanF PDFDocument34 pagesConférence AvellanF PDFceice2013No ratings yet
- Ognition PSV Sizing Calculation SpreadsheetDocument2 pagesOgnition PSV Sizing Calculation Spreadsheetrisqi ilham zulfahmiNo ratings yet
- Hydroelectric System Models: 3.1 Preliminary ConceptsDocument51 pagesHydroelectric System Models: 3.1 Preliminary ConceptsTilahun weldcherkosNo ratings yet
- Bottom Hole PressureDocument30 pagesBottom Hole PressuredinoNo ratings yet
- Gasdynamics AE4140 Chapter 1: IntroductionDocument60 pagesGasdynamics AE4140 Chapter 1: IntroductionPythonraptorNo ratings yet
- Refrigeration & Air Conditioning (MPE411) - Lec.2 - 2Document70 pagesRefrigeration & Air Conditioning (MPE411) - Lec.2 - 2Bassem OstoraNo ratings yet
- Section 12Document49 pagesSection 12Asad KhanNo ratings yet
- Hydropower Engineering: Turbines. Basic ConceptsDocument22 pagesHydropower Engineering: Turbines. Basic ConceptsHenrry RojasNo ratings yet
- Turbomachinery For Compressible FluidsDocument70 pagesTurbomachinery For Compressible FluidsArun BeniwalNo ratings yet
- Sistemas de Producción 11 - Curva de SalidaDocument59 pagesSistemas de Producción 11 - Curva de SalidaLuis Vallejo EstrellaNo ratings yet
- HVACR Formulas and SymbolsDocument46 pagesHVACR Formulas and SymbolsatiqNo ratings yet
- Mega Part2 cb1Document101 pagesMega Part2 cb1romy94496No ratings yet
- Civil Engineering FormulasDocument6 pagesCivil Engineering FormulasJonathan100% (3)
- Reciprocating+Compressors+ +3.+Useful+CorrelationsDocument17 pagesReciprocating+Compressors+ +3.+Useful+CorrelationsChristopherNo ratings yet
- Solved Problems in Soil Mechanics: SolutionDocument10 pagesSolved Problems in Soil Mechanics: SolutionMemo Ly100% (1)
- Lecture 26Document8 pagesLecture 2606me395No ratings yet
- Fundamentals of Compressible Flows in Pipelines: Dr. Ahmed Elmekawy Fall 2018Document74 pagesFundamentals of Compressible Flows in Pipelines: Dr. Ahmed Elmekawy Fall 2018Tamunoiboumie ElijahNo ratings yet
- ConvectionDocument26 pagesConvectionDozdiNo ratings yet
- Feuille Exercices Electrotechnique TDDocument3 pagesFeuille Exercices Electrotechnique TDanass sbniNo ratings yet
- 2.065/2.066 Acoustics and Sensing: Massachusetts Institute of TechnologyDocument12 pages2.065/2.066 Acoustics and Sensing: Massachusetts Institute of TechnologyKurran SinghNo ratings yet
- Part 10Document8 pagesPart 10Kerlos SaeedNo ratings yet
- Analysis of Compressible Flow in FUNDAMENTALS OF FLUID MECHANICSDocument210 pagesAnalysis of Compressible Flow in FUNDAMENTALS OF FLUID MECHANICSAjay kumar100% (1)
- Fundamentals of Fluid Mechanics Chapter 11 Analysis of Compressible FlowDocument210 pagesFundamentals of Fluid Mechanics Chapter 11 Analysis of Compressible FlowJake OkuyeNo ratings yet
- Topic 7 - Flow of Compressible FluidsDocument85 pagesTopic 7 - Flow of Compressible Fluidszairulh7No ratings yet
- Appendix C C. Formulae A. Chapter 1 Relations: E 2 - 14 3 2 2 2 E 24 E 6 2 C M 2 F Avog 26 26Document17 pagesAppendix C C. Formulae A. Chapter 1 Relations: E 2 - 14 3 2 2 2 E 24 E 6 2 C M 2 F Avog 26 26Ivelin ValchevNo ratings yet
- Surgetrol Tank SizingDocument1 pageSurgetrol Tank SizingAnonymous WpFsSj9sy1No ratings yet
- ME 4061 Compressible FlowDocument18 pagesME 4061 Compressible FlowFatih İnalNo ratings yet
- Crack Evaluation and Mitigation - CalculationDocument4 pagesCrack Evaluation and Mitigation - CalculationSilvioNo ratings yet
- Compressible Flow PDFDocument210 pagesCompressible Flow PDFRicky JuwonoNo ratings yet
- Rumus Head Loss BernoulliDocument2 pagesRumus Head Loss BernoulliZmique AzmiNo ratings yet
- Free Convection-9a PDFDocument16 pagesFree Convection-9a PDFSaeed AbdNo ratings yet
- Rigid conduit for fluid flow in two-phase fluid systems - MATLAB - MathWorks 中国Document6 pagesRigid conduit for fluid flow in two-phase fluid systems - MATLAB - MathWorks 中国944062528qqNo ratings yet
- PDF P324 06A (For Class) Lec Mod2 04a Diffusivity Eq (Orientation) PDFDocument18 pagesPDF P324 06A (For Class) Lec Mod2 04a Diffusivity Eq (Orientation) PDFvitaxnNo ratings yet
- Sample FormulasDocument6 pagesSample FormulasAhmedNo ratings yet
- 2900 - 4. FMEC Nozzle Theory PDFDocument46 pages2900 - 4. FMEC Nozzle Theory PDFMohmmmad HussainNo ratings yet
- Phys101 Term:121 Online HW-Ch14-Lec01Document2 pagesPhys101 Term:121 Online HW-Ch14-Lec01Amarjeet kaurNo ratings yet
- Assessment of Single-And Two-Zone Modeling of Centrifugal Compressors Studies in Component Performance: Part 3Document13 pagesAssessment of Single-And Two-Zone Modeling of Centrifugal Compressors Studies in Component Performance: Part 3khknimaNo ratings yet
- Calculation FD Fan PowerDocument7 pagesCalculation FD Fan PowerIrwansyah MuchtarNo ratings yet
- Analysis and Design of Transport Equipment: Anwar Ilmar Ramadhan, S.ST, MTDocument33 pagesAnalysis and Design of Transport Equipment: Anwar Ilmar Ramadhan, S.ST, MTEva AmeliaNo ratings yet
- Basic Drilling Engineering EquationsDocument6 pagesBasic Drilling Engineering EquationsFarah Omar FarahNo ratings yet
- Internal Flow: Heat Transfer CorrelationsDocument9 pagesInternal Flow: Heat Transfer CorrelationsbaroNo ratings yet
- SMD 1 2020 Z SNF HS CAL 0001 02 Safety Relief Valve Load Calculations (AutoRecovered)Document4 pagesSMD 1 2020 Z SNF HS CAL 0001 02 Safety Relief Valve Load Calculations (AutoRecovered)Amr TarekNo ratings yet
- Uniform Flow in Open Channels Economical SectionsDocument16 pagesUniform Flow in Open Channels Economical Sectionscarl ingariNo ratings yet
- Gas RateDocument2 pagesGas RateArif KhanNo ratings yet
- Engineering Calculation: (This Correlated Heat Transfer Coefficient at Tube Side Condition of Flow)Document3 pagesEngineering Calculation: (This Correlated Heat Transfer Coefficient at Tube Side Condition of Flow)RajdeepsinhNo ratings yet
- Kaplan Turbines SlidesDocument28 pagesKaplan Turbines Slidesjonas61700700100% (2)
- The Spectral Theory of Toeplitz Operators. (AM-99), Volume 99From EverandThe Spectral Theory of Toeplitz Operators. (AM-99), Volume 99No ratings yet
- Facts at Your Fingertips-201104-Hopper Inserts For Improved Solids FlowDocument1 pageFacts at Your Fingertips-201104-Hopper Inserts For Improved Solids Flowonizuka-t2263No ratings yet
- Facts at Your Fingertips-201105-Pressure Measurement ConsiderationsDocument1 pageFacts at Your Fingertips-201105-Pressure Measurement Considerationsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201101-Hansen Solubility Parameters (HSP)Document1 pageFacts at Your Fingertips-201101-Hansen Solubility Parameters (HSP)onizuka-t2263No ratings yet
- Facts at Your Fingertips-201007-Conservation Economics Carbon Pricing ImpactsDocument1 pageFacts at Your Fingertips-201007-Conservation Economics Carbon Pricing Impactsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201102-Control Valve Position SensorsDocument1 pageFacts at Your Fingertips-201102-Control Valve Position Sensorsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201010-MSMPR Crystallization EquipmentDocument1 pageFacts at Your Fingertips-201010-MSMPR Crystallization Equipmentonizuka-t2263No ratings yet
- Facts at Your Fingertips-201103-Infrared Temperature MeasurementDocument1 pageFacts at Your Fingertips-201103-Infrared Temperature Measurementonizuka-t2263No ratings yet
- Facts at Your Fingertips-201009-Controlling Membrane FoulingDocument1 pageFacts at Your Fingertips-201009-Controlling Membrane Foulingonizuka-t2263No ratings yet
- Facts at Your Fingertips-201011-Viscosity MeasurementDocument1 pageFacts at Your Fingertips-201011-Viscosity Measurementonizuka-t2263No ratings yet
- Facts at Your Fingertips-201005-Burner Operating Characteristics PDFDocument1 pageFacts at Your Fingertips-201005-Burner Operating Characteristics PDFonizuka-t2263No ratings yet
- Facts at Your Fingertips-201008-Heat Transfer Fluids System FiltrationDocument1 pageFacts at Your Fingertips-201008-Heat Transfer Fluids System Filtrationonizuka-t2263No ratings yet
- Facts at Your Fingertips-201012-Project Design Decision-Making Option ListsDocument1 pageFacts at Your Fingertips-201012-Project Design Decision-Making Option Listsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201003-Steam Tracer Lines and Traps PDFDocument1 pageFacts at Your Fingertips-201003-Steam Tracer Lines and Traps PDFonizuka-t2263No ratings yet
- Facts at Your Fingertips-200810-Heat TransferDocument1 pageFacts at Your Fingertips-200810-Heat Transferonizuka-t2263No ratings yet
- CHE Facts 0410Document1 pageCHE Facts 0410gwinnruNo ratings yet
- Facts at Your Fingertips-201002-Positive Displacement PumpsDocument1 pageFacts at Your Fingertips-201002-Positive Displacement Pumpsonizuka-t2263No ratings yet
- Facts at Your Fingertips-201005-Burner Operating Characteristics PDFDocument1 pageFacts at Your Fingertips-201005-Burner Operating Characteristics PDFonizuka-t2263No ratings yet
- Facts at Your Fingertips-200811-Alternative Fuels (Bio Diesel)Document1 pageFacts at Your Fingertips-200811-Alternative Fuels (Bio Diesel)onizuka-t2263No ratings yet
- Facts at Your Fingertips-200907-Flowmeter SelectionDocument2 pagesFacts at Your Fingertips-200907-Flowmeter Selectiononizuka-t2263No ratings yet
- Facts at Your Fingertips-200812-Fluid FlowDocument1 pageFacts at Your Fingertips-200812-Fluid Flowonizuka-t2263No ratings yet
- Facts at Your Fingertips-200809-CrystallizationDocument1 pageFacts at Your Fingertips-200809-Crystallizationonizuka-t2263No ratings yet
- Summary: Ionic EquilibriaDocument33 pagesSummary: Ionic Equilibriawewwchemistry100% (1)
- I V Savelyev Physics General Course Vol 3Document319 pagesI V Savelyev Physics General Course Vol 3thuongtunhienNo ratings yet
- Evaluation of Seismic Ground MotionDocument24 pagesEvaluation of Seismic Ground MotionmillzNo ratings yet
- Assignment No. 1Document9 pagesAssignment No. 1Cheryl Lou SantiagoNo ratings yet
- Stiffening Ring Cal For Exteneral Press.Document11 pagesStiffening Ring Cal For Exteneral Press.inspectormhp100% (1)
- Petrucci 11e PPT Ch07Document62 pagesPetrucci 11e PPT Ch07JOHN ZEDWIN STA. MONICANo ratings yet
- User Guide Sika Carbodur TR55Eurocode2 EnglishDocument52 pagesUser Guide Sika Carbodur TR55Eurocode2 EnglishMihaiNo ratings yet
- Polymer ProcessingDocument28 pagesPolymer ProcessingMousom SomNo ratings yet
- CH 16 Slides MDocument98 pagesCH 16 Slides MJennifer L. MadronioNo ratings yet
- Development of Processes For C4 Hydrocarbons SeparationDocument11 pagesDevelopment of Processes For C4 Hydrocarbons SeparationTasneem MNo ratings yet
- XII-NEET: 2021-22: Solutions Chemical EquilibriumDocument2 pagesXII-NEET: 2021-22: Solutions Chemical EquilibriumLalit KNo ratings yet
- Heat TreatmentDocument6 pagesHeat TreatmentjotikaNo ratings yet
- Temperature, Heat and The First Law of ThermodynamicsDocument3 pagesTemperature, Heat and The First Law of ThermodynamicspedroNo ratings yet
- GENCHM280 SolutionDocument58 pagesGENCHM280 SolutionReysel MonteroNo ratings yet
- Muthu Cad 2Document8 pagesMuthu Cad 2Sagarias AlbusNo ratings yet
- A Presentation ON Prototype: Dimensional Accuracy: Dr. D.Y PATIL College of Engineering Akurdi, Pune Maharashtra - 411044Document10 pagesA Presentation ON Prototype: Dimensional Accuracy: Dr. D.Y PATIL College of Engineering Akurdi, Pune Maharashtra - 411044AkshayJadhavNo ratings yet
- Total MixerDocument2 pagesTotal MixerFeroz KhanNo ratings yet
- Ultrasonics Sonochemistry: Bogdan NiemczewskiDocument6 pagesUltrasonics Sonochemistry: Bogdan NiemczewskiOmid7686No ratings yet
- Design of Plate Girder MCQDocument2 pagesDesign of Plate Girder MCQAvinash Kumar (RA1911001030001)No ratings yet
- Vibration IsolationDocument8 pagesVibration Isolationofitecnicajg100% (1)
- Investigatory Project Physics by RonitDocument17 pagesInvestigatory Project Physics by RonitronitsuniyaNo ratings yet
- Bafer 100.VE.06 PDFDocument61 pagesBafer 100.VE.06 PDFVasiljka Đordan JelacaNo ratings yet
- Cambridge IGCSE: Physics 0625/23Document20 pagesCambridge IGCSE: Physics 0625/23Manya PunjabiNo ratings yet
- Formulation and Evaluation of Microemulsion Based Gel of KetoconazoleDocument19 pagesFormulation and Evaluation of Microemulsion Based Gel of KetoconazoleAndre HopfnerNo ratings yet
- Transformation of Electrical EnergyDocument8 pagesTransformation of Electrical EnergyAnaluz Redondo GoleñaNo ratings yet
- 5a - PumpTraining 032306Document32 pages5a - PumpTraining 032306Islam SolimanNo ratings yet
- LN - 10 - 51 - E-Learning Hydrological CycleDocument8 pagesLN - 10 - 51 - E-Learning Hydrological CycleMaria OzaoNo ratings yet
- Chapter 16 Radiation Protection and Safety PDFDocument236 pagesChapter 16 Radiation Protection and Safety PDFAshutosh SinghNo ratings yet