Cambridge IGCSE Mathematics Core and Extended CD-ROM

Core questions: 1 – 3
Extended questions: 4 – 9

Extended revision exercises: Algebra

Worksheet 18: Curved graphs
1 Construct a table of values, selecting values from 6  x  6 , for each of the following equations. Draw
the graphs on the same set of axes.
(a) y   x 2  3 (b) y  x 2  2 x  2 (c) y  x 2  8x  16

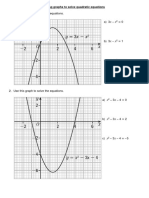
2 This is the graph of y  x 2  4 x  3 .

Use the graph to estimate the solution of:
(a) x 2  4 x  3  0

(b) x 2  4 x  3  3
(c) x 2  4 x  1

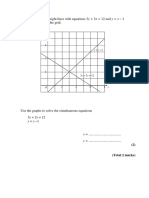
3 By drawing up a table of values, and drawing the graphs on the same set of axes, find the approximate
solutions to the simultaneous equations 2 y  x  1 and y  x 2  4 x  3 .

4 For each of the following:

(a) complete the table of values for each equation
(b) use the points to plot each graph on a separate set of axes.
x –5 –4 –3 –2 –1 1 2 3 4 5
2
y
x

x –5 –4 –3 –2 –1 1 2 3 4 5
xy  1

x –1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5

y  x3  2 x

x –1 –0.5 0 0.5 1 1.5 2 2.5

1
y  2  x2 
x

Original material © Cambridge University Press 2015 1

 Cambridge IGCSE Mathematics Core and Extended CD-ROM

5 The graph of y  2 x 2  4 x  5 is shown on the grid.

Find the gradient of the graph:
(a) where x  2
(b) where x  2 .

6 Draw the graph of y  x 2  2 x  5 .

(a) Find the gradient of the graph at the points:
(i) (3, –2) (ii) (–2, 3)
(b) Use the graph to solve the equation x 2  2 x  7  0 .

7 (a) Draw the graph of y = 2x2 + x – 3 for –3 ≤ x ≤ 2.

(b) Use the graph to estimate the solutions to the equation 2x2 + x – 3 = 0.
(c) On the same axes above draw the line with equation y = 2x + 1.
(d) Write down the co-ordinates of all points on intersection between the two graphs.
(e) Explain why the x co-ordinates of the points of intersection are, in fact, the solutions to the equation
2x2 – x – 4 = 0.

8 (a) Draw the graph of y = x2 – 2x + 3 for –2 ≤ x ≤ 4.

(b) By drawing a suitable line on the same graph, solve the equation x2 – 2 = 0.
(c) Hence, without using a calculator state the approximate value of the square root of 2.

9 (a) Draw a careful graph of y = x2 for –2 ≤ x ≤ 2.

(b) On the same diagram draw the graph of y = 2x – 1.
(c) Use the graph to solve the equation x2 – 2x + 1 = 0.
(d) What is significant about the line y = 2x – 1?
(e) What is the gradient of the curve y = x2 at the point where x = 1?

Original material © Cambridge University Press 2015 2