Professional Documents
Culture Documents
Questions To Guide Your Review: B 2, B P 3. C 2, B P 3. y 1 + Sin Ax + P
Questions To Guide Your Review: B 2, B P 3. C 2, B P 3. y 1 + Sin Ax + P
Uploaded by
Cyn Syjuco0 ratings0% found this document useful (0 votes)
41 views2 pagesThe document provides examples of problems involving right triangles and their trigonometric functions. It includes problems about expressing sides of a right triangle in terms of angles and other sides, finding heights using trigonometric ratios, and graphing trigonometric functions. It also provides review questions to guide studying preliminaries in mathematics.
Original Description:
sample
Original Title
temp2
Copyright
© © All Rights Reserved
Available Formats
DOCX, PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThe document provides examples of problems involving right triangles and their trigonometric functions. It includes problems about expressing sides of a right triangle in terms of angles and other sides, finding heights using trigonometric ratios, and graphing trigonometric functions. It also provides review questions to guide studying preliminaries in mathematics.
Copyright:
© All Rights Reserved
Available Formats
Download as DOCX, PDF, TXT or read online from Scribd
Download as docx, pdf, or txt
0 ratings0% found this document useful (0 votes)
41 views2 pagesQuestions To Guide Your Review: B 2, B P 3. C 2, B P 3. y 1 + Sin Ax + P
Questions To Guide Your Review: B 2, B P 3. C 2, B P 3. y 1 + Sin Ax + P
Uploaded by
Cyn SyjucoThe document provides examples of problems involving right triangles and their trigonometric functions. It includes problems about expressing sides of a right triangle in terms of angles and other sides, finding heights using trigonometric ratios, and graphing trigonometric functions. It also provides review questions to guide studying preliminaries in mathematics.
Copyright:
© All Rights Reserved
Available Formats
Download as DOCX, PDF, TXT or read online from Scribd
Download as docx, pdf, or txt
You are on page 1of 2
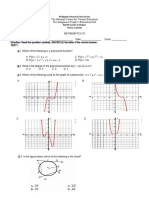
In Exercises 75–78, ABC is a right triangle with the right angle at C.
The sides opposite angles A, B, and C are a, b, and c, respectively.
75. a. Find a and b if
b. Find a and c if
76. a. Express a in terms of A and c.
b. Express a in terms of A and b.
77. a. Express a in terms of B and b.
b. Express c in terms of A and a.
78. a. Express sin A in terms of a and c.
b. Express sin A in terms of b and c.
79. Height of a pole Two wires stretch from the top T of a vertical
pole to points B and C on the ground, where C is 10 m closer to
the base of the pole than is B. If wire BT makes an angle of 35°
with the horizontal and wire CT makes an angle of 50° with the
horizontal, how high is the pole?
80. Height of a weather balloon Observers at positions A and B
2 km apart simultaneously measure the angle of elevation of a
weather balloon to be 40° and 70°, respectively. If the balloon is
directly above a point on the line segment between A and B, find
the height of the balloon.
81. a. Graph the function
b. What appears to be the period of this function?
c. Confirm your finding in part (b) algebraically.
82. a. Graph
b. What are the domain and range of ƒ?
c. Is ƒ periodic? Give reasons for your answer.
ƒsxd = sin s1>xd .
ƒsxd = sin x + cossx>2d .
b = 2, B = p>3.
c = 2, B = p>3.
y = 1 + sin ax + p
4
b.
y = 2 cos ax - p
3
b.
y = cos
px
2
y = sin px
y = sin
x
2
y = cos 2x
x2 + x ƒ x2 + x ƒ
ƒ 4 - x2 4 - x2 ƒ
2x ƒ 2x ƒ
ƒ x3 x3 ƒ
g1sxd g2sxd _ ƒ g1sxd ƒ
g1
g2
g1
70 Chapter 1: Preliminaries
T
T
68 Chapter 1: Preliminaries
Chapter 1 Questions to Guide Your Review
1. How are the real numbers represented? What are the main categories
characterizing the properties of the real number system?
What are the primary subsets of the real numbers?
2. How are the rational numbers described in terms of decimal expansions?
What are the irrational numbers? Give examples.
3. What are the order properties of the real numbers? How are they
used in solving equations?
4. What is a number’s absolute value? Give examples? How are
and related to and
5. How are absolute values used to describe intervals or unions of
intervals? Give examples.
6. How do we identify points in the plane using the Cartesian coordinate
system? What is the graph of an equation in the variables x
and y?
7. How can you write an equation for a line if you know the coordinates
of two points on the line? The line’s slope and the coordinates
of one point on the line? The line’s slope and y-intercept?
Give examples.
8. What are the standard equations for lines perpendicular to the coordinate
axes?
9. How are the slopes of mutually perpendicular lines related? What
about parallel lines? Give examples.
10. When a line is not vertical, what is the relation between its slope
and its angle of inclination?
11. How do you find the distance between two points in the coordinate
plane?
12. What is the standard equation of a circle with center (h, k) and radius
a? What is the unit circle and what is its equation?
13. Describe the steps you would take to graph the circle
14. What inequality describes the points in the coordinate plane that
lie inside the circle of radius a centered at the point (h, k)? That
lie inside or on the circle? That lie outside the circle? That lie outside
or on the circle?
15. If a, b, and c are constants and what can you say about the
graph of
You might also like
- Genki - An Integrated Course in Elementary Japanese Answer Key (Second Edition) (2011, E. Banno, Y. Ikeda, Y. Ohno, C. Shinagawa, K. Tokashiki)Document86 pagesGenki - An Integrated Course in Elementary Japanese Answer Key (Second Edition) (2011, E. Banno, Y. Ikeda, Y. Ohno, C. Shinagawa, K. Tokashiki)AdlebertCoalseed85% (228)
- 2012-2013 Quarter 1 - 5th Grade Math RubricDocument4 pages2012-2013 Quarter 1 - 5th Grade Math Rubricnelly_marlina02100% (1)
- Convex AnalysisDocument30 pagesConvex AnalysisFranklin GálvezNo ratings yet
- PM 2Document289 pagesPM 2danielrita570No ratings yet
- Pre-Test Precalculus Grade 11-Stem: DIRECTION: Read Each Statement Carefully. Choose The Correct Answer From TheDocument5 pagesPre-Test Precalculus Grade 11-Stem: DIRECTION: Read Each Statement Carefully. Choose The Correct Answer From TheCarrie Lhee BoadoNo ratings yet
- Math 10 Q2Document5 pagesMath 10 Q2AprilJoanAbianChuaNo ratings yet
- L2-4 Select Qs (Unit 6 - Mid-Unit Practice)Document5 pagesL2-4 Select Qs (Unit 6 - Mid-Unit Practice)tegaogaga400No ratings yet
- Grade 10 Math PretestDocument2 pagesGrade 10 Math Pretestadelfa.montesNo ratings yet
- Analytic Geometry and Differential and Integral CalculusDocument166 pagesAnalytic Geometry and Differential and Integral CalculusOnline EducatorNo ratings yet
- Hb3Dxxxxxfffffff6Yrepublic of PhilippinesDocument5 pagesHb3Dxxxxxfffffff6Yrepublic of PhilippinesGirlie Mae Drilon FloresNo ratings yet
- Math and ApDocument7 pagesMath and ApjoannaNo ratings yet
- Summative TestDocument7 pagesSummative TestJulianna Marie ConcepcionNo ratings yet
- 3rd PT 22-23Document3 pages3rd PT 22-23Faye LouraneNo ratings yet
- 2nd Quarter Assessment Math 10Document7 pages2nd Quarter Assessment Math 10Erick DiosoNo ratings yet
- Geometry Trigonometry HardDocument71 pagesGeometry Trigonometry HardAnar AnarNo ratings yet
- Analytic GeometryDocument110 pagesAnalytic GeometryAsagiri, Kishi D.No ratings yet
- Engineering Mechanics (1000 MCQS)Document199 pagesEngineering Mechanics (1000 MCQS)IyfiyffiiyvNo ratings yet
- Analytic Geometry and Differential and Integral CalculusDocument330 pagesAnalytic Geometry and Differential and Integral CalculusJOHN CHRISTOPHER GABONNo ratings yet
- Geometry McqsDocument8 pagesGeometry Mcqsshahrupesh1212No ratings yet
- 2nd Quarter PT Math10Document5 pages2nd Quarter PT Math10Renato PanesNo ratings yet
- Mathematics 8Document5 pagesMathematics 8Florinda CorpuzNo ratings yet
- Summative Test No. 2geometryDocument8 pagesSummative Test No. 2geometryモーラーリー いたちNo ratings yet
- G10 MATH 2nd QTRDocument2 pagesG10 MATH 2nd QTRJo Mai HannNo ratings yet
- Assignment 1Document3 pagesAssignment 1KuthuraikaranNo ratings yet
- ACT MATH Practice Paper 3Document14 pagesACT MATH Practice Paper 3SSNo ratings yet
- Maths sylabbusICSE Class 10 Maths SyllabusDocument8 pagesMaths sylabbusICSE Class 10 Maths Syllabusprash_hingeNo ratings yet
- ICSE Class 10 Maths SyllabusDocument8 pagesICSE Class 10 Maths Syllabusprash_hingeNo ratings yet
- CDS II 2020 Mathematics: WWW - Gradeup.coDocument22 pagesCDS II 2020 Mathematics: WWW - Gradeup.coSR SNo ratings yet
- Summative Test 2.4Document2 pagesSummative Test 2.4Jaymar SarvidaNo ratings yet
- PT-2, Maths, Class-X, 2022-23, RKSDocument6 pagesPT-2, Maths, Class-X, 2022-23, RKScuriousnavinNo ratings yet
- Post ExamDocument13 pagesPost ExamKeith Madarang100% (1)
- Module 1 SSP Math 10Document11 pagesModule 1 SSP Math 10Chriza SuarezNo ratings yet
- Euclid Contest: The Centre For Education in Mathematics and Computing Cemc - Uwaterloo.caDocument6 pagesEuclid Contest: The Centre For Education in Mathematics and Computing Cemc - Uwaterloo.caAndre YunusNo ratings yet
- Grade 10 Formative Test CircleDocument14 pagesGrade 10 Formative Test CircleReygie Fabriga100% (3)
- G10 Q2 PretestDocument2 pagesG10 Q2 PretestSean Akki GumatayNo ratings yet
- Mathematics: Quarter 2 - Module 5: Secants, Tangents, Segments and Sectors of A CircleDocument18 pagesMathematics: Quarter 2 - Module 5: Secants, Tangents, Segments and Sectors of A CircleJay Vincent MacadangdangNo ratings yet
- Chapter 8 CoordinatesDocument15 pagesChapter 8 CoordinatesMadihah RamlyNo ratings yet
- Additional Topics Practice Test NewDocument11 pagesAdditional Topics Practice Test NewSahyogNo ratings yet
- 2nd Quarter Examination in Mathematics 10Document5 pages2nd Quarter Examination in Mathematics 10Norman A ReyesNo ratings yet
- 3RD Quarter - Summative 1Document2 pages3RD Quarter - Summative 1Aimee Acedera PuertaNo ratings yet
- Gadu National High School - Nangalisan Extension Second Periodic Test Math 10 MULTIPLE CHOICE: Choose The Letter of The Best AnswerDocument3 pagesGadu National High School - Nangalisan Extension Second Periodic Test Math 10 MULTIPLE CHOICE: Choose The Letter of The Best AnswerTito Agoo100% (1)
- Answer Key For Summative TestDocument53 pagesAnswer Key For Summative TestAnimeNo ratings yet
- 2nd Test Math 10Document4 pages2nd Test Math 10Josefina TabatNo ratings yet
- WK 7-8 - Using The Distance Formula in Proving Geometric Properties & Equation of A Circle Center at The OriginDocument38 pagesWK 7-8 - Using The Distance Formula in Proving Geometric Properties & Equation of A Circle Center at The OriginJENNALYN RESARENo ratings yet
- 3rd Periodical Test in Mathematics 7Document5 pages3rd Periodical Test in Mathematics 7sineNo ratings yet
- LinesDocument27 pagesLinesicynitrogen9087No ratings yet
- Post Test in Mathematics 7Document8 pagesPost Test in Mathematics 7zaldy mendozaNo ratings yet
- Syjmxc 5 P 9 VBo 4 J REz AG4Document6 pagesSyjmxc 5 P 9 VBo 4 J REz AG4chanti malothNo ratings yet
- Ignite Tuition-WPS OfficeDocument26 pagesIgnite Tuition-WPS OfficeSarkar BapanNo ratings yet
- Taller Parcial 2 2019 II P1Document3 pagesTaller Parcial 2 2019 II P1RAUL GUERRANo ratings yet
- I. Vectors and Geometry in Two and Three DimensionsDocument31 pagesI. Vectors and Geometry in Two and Three DimensionsMasAmirahNo ratings yet
- AP Physics 1 Summer PacketDocument14 pagesAP Physics 1 Summer PacketAkhil DonapatiNo ratings yet
- GEOMETRYDocument9 pagesGEOMETRYLimar Anasco EscasoNo ratings yet
- ELECTIVE-MATHEMATICS-10-Module-3 Analytic ProofsDocument21 pagesELECTIVE-MATHEMATICS-10-Module-3 Analytic ProofsFVERON, JESSICA FABELLORENo ratings yet
- Analytic GeometryDocument110 pagesAnalytic Geometryeric salesNo ratings yet
- Test Question Math 10Document4 pagesTest Question Math 10marjorie antonioNo ratings yet
- Math Aptitude QuestionsDocument4 pagesMath Aptitude QuestionsShilpa PrabhakarNo ratings yet
- Unit 4 GeometryDocument5 pagesUnit 4 GeometryAzista PharmaNo ratings yet
- геометрия синфи 11Document16 pagesгеометрия синфи 11Biloljon MuminovNo ratings yet
- GMAT Geometry Worksheet - 2D, 3D and Coordinate GeometryDocument13 pagesGMAT Geometry Worksheet - 2D, 3D and Coordinate Geometryk.saikumarNo ratings yet
- M44 Polar Circles - EkPolarCoordDocument6 pagesM44 Polar Circles - EkPolarCoordNoraNo ratings yet
- Need Ko Lang Mag DLDocument6 pagesNeed Ko Lang Mag DLDollesin Joseph Jr.No ratings yet
- Math 10Document3 pagesMath 10Romeo Jr Pacheco Opena50% (2)
- Whistleblowing PolicyDocument3 pagesWhistleblowing PolicyCyn SyjucoNo ratings yet
- Exercises: Section 32.2 Plane Electromagnetic Waves and The Speed of LightDocument3 pagesExercises: Section 32.2 Plane Electromagnetic Waves and The Speed of LightCyn SyjucoNo ratings yet
- Rates of Change and Limits: Average and Instantaneous SpeedDocument2 pagesRates of Change and Limits: Average and Instantaneous SpeedCyn SyjucoNo ratings yet
- Average Rates of ChangeDocument3 pagesAverage Rates of ChangeCyn SyjucoNo ratings yet
- Salary Advance Agreement - 1Document1 pageSalary Advance Agreement - 1Cyn SyjucoNo ratings yet
- Exercises: Section 1.3 Standards and Units Section 1.4 Unit Consistency and ConversionsDocument1 pageExercises: Section 1.3 Standards and Units Section 1.4 Unit Consistency and ConversionsCyn SyjucoNo ratings yet
- SAMPLE: Emergency Response Plan: Minor EmergenciesDocument3 pagesSAMPLE: Emergency Response Plan: Minor EmergenciesCyn SyjucoNo ratings yet
- 03 Alcohol Free Workplace Policy ProgramDocument3 pages03 Alcohol Free Workplace Policy ProgramCyn SyjucoNo ratings yet
- San Francisco Premium Outlets FreeSavingsPassportVoucher 032017 PDFDocument1 pageSan Francisco Premium Outlets FreeSavingsPassportVoucher 032017 PDFCyn SyjucoNo ratings yet
- Starbucks 2014 Investor Day - Financial OverviewDocument16 pagesStarbucks 2014 Investor Day - Financial OverviewCyn SyjucoNo ratings yet
- Beads Couture Tambour BeadingDocument58 pagesBeads Couture Tambour BeadingCyn SyjucoNo ratings yet
- Waiting Line ModelsDocument46 pagesWaiting Line ModelsCyn SyjucoNo ratings yet
- Applying Motivation Theory: Presented By: Gheng Castillo Mej Lauron Neil Peralta Joni Tugna Paolo WenceslaoDocument27 pagesApplying Motivation Theory: Presented By: Gheng Castillo Mej Lauron Neil Peralta Joni Tugna Paolo WenceslaoCyn SyjucoNo ratings yet
- Educational Psychology: Developed by W. Huitt, 1999Document21 pagesEducational Psychology: Developed by W. Huitt, 1999Cyn SyjucoNo ratings yet
- Final Project Paper Format: By: Juanito S. ChanDocument3 pagesFinal Project Paper Format: By: Juanito S. ChanCyn SyjucoNo ratings yet
- Chap 004Document36 pagesChap 004Cyn SyjucoNo ratings yet
- As G481 MechanicsDocument69 pagesAs G481 MechanicsCyn Syjuco0% (1)
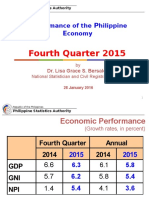
- Q4 2015 NAP Short With PSA LogoDocument8 pagesQ4 2015 NAP Short With PSA LogoCyn SyjucoNo ratings yet
- Modaris CAD 2 Lectra - Specialist Weekly CourseDocument2 pagesModaris CAD 2 Lectra - Specialist Weekly CourseCyn SyjucoNo ratings yet
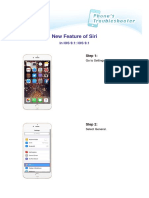
- New Feature of Siri (IOS 9.1 - IOS 9.1)Document4 pagesNew Feature of Siri (IOS 9.1 - IOS 9.1)Cyn SyjucoNo ratings yet
- Highlights Q4 2015Document12 pagesHighlights Q4 2015Cyn SyjucoNo ratings yet
- Rob HW3Document1 pageRob HW3Cyn SyjucoNo ratings yet
- Chapter 11 Managing ChangeDocument48 pagesChapter 11 Managing Changepolkadots939100% (6)
- First Year Micro Project Maths SubjectDocument3 pagesFirst Year Micro Project Maths SubjectSwayam ChaulkarNo ratings yet
- Vii-Simple EquatiosDocument36 pagesVii-Simple EquatiosSudheer KumarNo ratings yet
- Fixed Point Theory and Best Approximation: The KKM-map PrincipleDocument230 pagesFixed Point Theory and Best Approximation: The KKM-map PrincipleFranklin GálvezNo ratings yet
- Textbook Basic Algebra Anthony W Knapp 3 Ebook All Chapter PDFDocument40 pagesTextbook Basic Algebra Anthony W Knapp 3 Ebook All Chapter PDFhershel.beach855100% (22)
- 1Document7 pages1Suraj MoteeNo ratings yet
- Addmath F4C1 Functions (Raya Class '23)Document15 pagesAddmath F4C1 Functions (Raya Class '23)CHAN CHING AI MoeNo ratings yet
- Relation and FunctionDocument4 pagesRelation and FunctionHemendra PrasannaNo ratings yet
- Wave FunctionsDocument10 pagesWave FunctionsDavid ChangNo ratings yet
- ITF Errorless-1Document9 pagesITF Errorless-1ashmitaramoliya123No ratings yet
- Mathematics Extension 2 HSC LevelDocument250 pagesMathematics Extension 2 HSC LevelkalstarNo ratings yet
- Lesson-2 Evaluating-Functions PDFDocument18 pagesLesson-2 Evaluating-Functions PDFDiaz, Jaire Michael S. 11 HUMMS-6No ratings yet
- Numerical Analysis II PDFDocument115 pagesNumerical Analysis II PDFAlaa GhaziNo ratings yet
- Bus Impedance MatrixDocument22 pagesBus Impedance MatrixChristine Mae Barola100% (1)
- Business Math PDFDocument32 pagesBusiness Math PDFsabbir ahmed100% (1)
- Important Polynomials QuestionsDocument5 pagesImportant Polynomials QuestionsSoham ChakrabortyNo ratings yet
- Phy10 Wk01 Vector 1Document69 pagesPhy10 Wk01 Vector 1Jed Efraim EspanilloNo ratings yet
- 4 Systems of Linear EquationsDocument4 pages4 Systems of Linear EquationsZidarNo ratings yet
- Answers: (Lesson 5-1 and Lesson 5-2)Document18 pagesAnswers: (Lesson 5-1 and Lesson 5-2)Mazahir Mohammad BakirNo ratings yet
- US Army Medical Course MD0837-200 - Laboratory MathematicsDocument185 pagesUS Army Medical Course MD0837-200 - Laboratory MathematicsGeorgesNo ratings yet
- Differential Equations: Md. Dalim Haque Department of Mathematics RUET, Bangladesh .: 01774015578Document19 pagesDifferential Equations: Md. Dalim Haque Department of Mathematics RUET, Bangladesh .: 01774015578salehmashrur 98No ratings yet
- Topics No. of Class Session Percentage (%) Level No. of Items Item Placement K P UDocument1 pageTopics No. of Class Session Percentage (%) Level No. of Items Item Placement K P UMariel EfrenNo ratings yet
- MATH 1003 Calculus and Linear Algebra (Lecture 8) : Albert KuDocument22 pagesMATH 1003 Calculus and Linear Algebra (Lecture 8) : Albert KuMFong ThongNo ratings yet
- 0580 s15 Ms 21 PDFDocument5 pages0580 s15 Ms 21 PDFCiaoNo ratings yet
- 2019 FY12 CEMathematics Detailed SolutionsDocument19 pages2019 FY12 CEMathematics Detailed SolutionsSelina VuninaiNo ratings yet
- 2017 Tle 7 Week 6Document25 pages2017 Tle 7 Week 6RUDYARD DELA PEŇA100% (2)
- Derivatives #3Document49 pagesDerivatives #3tolgonai2705No ratings yet
- Vector 2 Comprehensive Notes - by TrockersDocument117 pagesVector 2 Comprehensive Notes - by TrockersDaisy Kachivemba100% (2)