| Stress Analysis Symbols Description and Units A cross sectional area, mm? A, area under shear, mm? e distance from neutral axis to the extreme fibre, mm E modulus of elasticity or young’s modulus, MN/m?(kgf/mm?) e eccentricity, as of force application, mm F force, N(kgf) F, direct shear force, N(kgf) FF; critical load that will cause rupture, Nkgf) G modulus of rigidity, MN/m?(kgf/mm2) 7 Z rectangular and polar moment of inertia respectively, mm* k radius of gyration of cross-section, mm M bending moment, N-mm(kgf-mm) R radius of curvature, mm T torque or torsional moment, N-mm(kgf-mm) Z,Z, rectangular and polar section modulus respectively, mm? a the coefficient of linear expansion, mm/mm/K(mm/mm/?C) y shearing Strain, rad/mm 6 axial deformation or total elongation, mm. & angular deformation, rad € strain or deformation per unit length, mm/mm €. 6+ € strain due only to stresses in the x, y, z directions respectively, mm/mm “ poisson’s ratio oD stress, direct or normal, tensile or compression, MN/m? (kgf/mm) o stress, MN/m? (kgf/mm?) x,y, Oz normal stresses in x, y, z directions respectively, MN/m? (kgf/mm?) maximum and minimum normal stresses respectively, MN/m? (kgf/mm?)Stress Analysis Description and Units A cross sectional area, mm? A, area under shear, mm? ¢ distance from neutral axis to the extreme fibre, mm E modulus of elasticity or young’s modulus, MN/m?(kgf/mm?) e eccentricity, as of force application, mm F force, N(kef) F, direct shear force, N(kgf) Fe, critical load that will cause rupture, N¢kgt) G modulus of rigidity, MN/m?(kgf/mm?) nS rectangular and polar moment of inertia respectively, mm* k Tadius of gyration of cross-section, mm M bending moment, N-mm(kgf-mm) R radius of curvature, mm r torque or torsional moment, N-mm(kgf-mm) ZZ», rectangular and polar section modulus respectively, mm? @ the coefficient of linear expansion, mm/mm/K(mm/mm/*C) y shearing Strain, rad/mm axial deformation or total elongation, mm 5, angular deformation, rad € strain or deformation per unit length, mm/mm <6, € strain due only to stresses in the x, y, z directions respectively, mm/mm H poisson’s ratio oD stress, direct or normal, tensile or compression, MN/m? (kgf/mm?) o stress, MN/m? (kgf/mm?) normal stresses in x, y, z directions respectively, MN/m? (kgf/mm?) maximum and minimum normal stresses respectively, MN/m?(kgf/mm?)Symbols Description and Units yp _tensile stress at yield point, MN/m?(kgf/mm?) Oe stress at the elastic limit, MN/m?(kgf/mm?) t shear stress, MN/m?(kgf/mm?) 7 shear stress, x and y direction, MN/m?(kgf/mm?) = ey shear stress at yield point, MN/m? (kgf/mm?) tp direct shear stress, MN/m? (kgf/mm?) Particular Equation Eqn. No. Simple Stresses and Strains: ‘The direct stress in simple tension or yeti af 1A@ compression. Fig. 1.1(a) Maximum Bending stress at point P. pron Me MRM Re 1.10) Fig. 1.1(b) ad Direct shear stress. Fig. 1.1(c) Tp=t= a 11©) (Maximuns Totsional sheer guest. Fi et 11@) 72, Strain or deformation per unit length due to | € = ¢ = <= 1.2) direct axial load Fig. 1.1(a): Direct stress —| Fy ! +See | foot a ’ cs, Fr Mga” Fig. 1.1(c): Direct shear stress Fig. 1.1(d): Torsional shear stressSwess Analysis Particular Equation Eqn. No. Deformation or Total elongation of a member | 6 = = a 1.2(b) See to direct axial load where ‘L’ is the length of the bar, mm ‘Shear strain due to direct shear force (radians) | r = z 1.2(6) he general bending equation 4 2 ; =< 1.3() ‘The general torsion equation t e = : 1.3() i . TL The angle of twist ina shaft subjected toa — | @ = 7 13(¢) ‘Sergue (radians) Combined Stresses: @ Combined axial and Bending loads Fie 12a) ‘The maximum normal stress due to combined 14 ‘=xial and bending loads (super position) @& Combined axial, bending and torsional Seads (Fig. 1.2(b), 1.2(c) and 1.2(4)] According to maximum normal stress theory | max = $ + (5) +r 1.5(a) ot According to maximum shear stress theory | Tmax = (5) z 1.5(b) loads (T = 0) Fig. 1.2(b): Combined axial and torsional loads (F; = 0) Fig. 1.2(¢): Combined torsional and bending loads (F, = 0) Fig. 1.2(d): Combined axial, bending and torsional loadsStress Analysis Particular Equation Eqn. No. . : oL_ FL Deformation or Total elongation of a member | 6 = [= = == 1.20) due to direct axial load where ‘L’ is the length of the bar, mm Shear strain due to direct shear force (radians) | r= = 1.200) : ; M_E_o ‘The general bending equation TRE 1.3(a) f T_Go_t . ‘The general torsion equation 57a 1.300) ~ TL The angle of twist in a shaft subjected toa | @ = <= 13) IG torque (radians) Combined Stresses: () Combined axial and Bending loads (Fig. 1.2(a)) The maximum normal stress due to combined | Gina = Op +05 = 0 = : iY a 14 axial and bending loads (super position) (ii) Combined axial, bending and torsional loads (Fig. 1.2(b), 1.2(c) and 1.2(4)] 5 According to maximum normal stress theory (5) +? 1.5(a) ma According to maximum shear stress theory | Tmax = () +r 1.5(b) loads (T = 0) Fig. 1.2(c): Combined torsional and bending loads (F, = 0) Fig. 1.2(b): Combined axial and torsional loads (F; = 0) Fig. 1.2(d): Combined axial, bending and torsional loads its4 Stress Analysis Particular Equation Eqn. No. Compound Stresses: (@) Uniaxial stress system [Fig. 1.3(a)] The normal stress in the plane at any desired | cr, = cos? = 0 cos? g 1.6(a) angle The shear stress at any desired angle T= = sin 2g = — sin2g 1.6(b) The principal stresses (o = 0) and (o) = 0) 1.6(c) Direction of principal stresses 1 =0° 16a) Maximum shear stress at 45° Tmax = S 1.6(e) Direction of maximum shear stress $5, = 45° 16(f) (ii) Biaxial stress system (Fig. 1.3(b)] Trt Oy) [ox-y The normal stress in the plane at any desired | ory ( a) ( Jeos2p —1.71@) 2 2 angle é o~oy The shear stress at any desired angle @ Ta ( ) sin2g 1.70) = The principal stresses (7 = oy) and (oy = 0) 1.76) a Direction of principal stresses (@) = 0°) and (> = 90°) 17) E i + By a Maximum shear stress at ¢ = 45 a= ( x)= Le) Direction of maximum shear stress 4s, = 45° and bs, = 135° 176) Resultant stress (Fig. 1.3(b)) o= Vorre 178) 4 Direction of resultant stress (Fig. 1.3(b)) tan6 = ( =) 1.7(h) i o iB a o o=al & ce a Fi = i 4 A AT oy 03 oy = 02 Fig. 1.3(a): Uniaxial stress system Fig. 1.3(b): Biaxial stress systemStress Analysis 5 Particular Equation Eqn. No. (ili) Plane stress system [Fig. LA(a)] . ; Or+Oy) . [Ox—0 The normal stress in the plane at any desired on = (SS) +( ; Jeos2s anzle ¢ +t sin26 1.8(a) ‘ Oxr-Oy\) . The shear stress at any desired angle ¢ m= ( + ) sin29 = Ty cos 26 1.8(b) Sse Maximum principal stress. oe ()+ (—) +7, 1800) al Minimum principal stress = (2) 2 (= 5 2) +7, 18(d) 2try Direction of principal stress [Fig. 1.4(b)] tan 24, = (=) 1.8(e) 1 Oy Maximum shear stress Lat) Direction of shear stress (Fig. 1.4(c)] tan(24,) = ( a ) 1.8(g) Direction of maximum shear stress 6, max = 61 + 45° Direction of minimum shear stress 6, min = $1 + 135° |X Fig. 1.4(a): Plane stress system Tay x (3%) Fig, 1.4(b): Direction of principal stress Fig. 1.4(e): Direction of shear stressStress Analysis Particular Equation Eqn. No. Mohr’s circle diagram: Fig. 1.5(a) and 1.5(b) Equation for the Mohr’s circle diagram Equation for the Mohr’s circle diagram (« - Set Oo) = (252) Hen? 19) (on- OF +7? = Rt 1.90) which is the equation of a circle Where C = 22% 7 1.9) 1.9%@) ty Fig. 1.5(a): Plane stress system OA = or,, Stress in x-direction OB = cy, Stress in y-direction AD = BE = Ty, Shear stress OF =o, Maximum principal stress OG = o72, Minimum principal stress CH = Tax. Maximum shear stress \D(o2,72y) Fig. 1.5(b): Mohr’s circle diagram for plane stress 00 = on, Normal stress PQ =r, Tangential stress OP = o, Resultant Stress 12DCF = 61, Direction of Max principal stress 42DCB = 6 = $1 +90°, directing Min principal stress 12HCF = $s,, Direction of Maximum shear stressStress Analysis Particular Equation Superposition: (Eccentric loading) (Fig. 1.6) Maximum normal stress due to direct tension ee compression combined with bending Biaxial deformation:— (Fig. 13(b)) Poisson's ratio Resultant unit deformation or strain in the E-direction Resultant unit deformation or strain in the F direction Stresses in terms of strains: ‘The normal stress in the X-direction ‘The normal stress in the Y-direction Triaxial deformations: (Fig. 1.7(b)) Resultant unit deformation or strain in the E-direction Resultant strain in the Y-direction Resultant strain in the Z-direction Relation between the constants E, G and y for 2 given material ce 1.10 “ 1.11 (a) & 1.11(b) gm 2 = LHe) = eau 1.) (6 + HEE - eo L.11(e) Hoy +o.) 1.12¢a) 1 6= glo He + 0] 1.12(b) Ele: -Ho, + 03)| 1.12(¢) E 20+) ee) Oo: [selec 4 Le. Up (a) With no shear stress Fig. 1.6: Eccentric load (b) With shear stress Fig, 1.7: Triaxial stress system‘Stress Particular Equation Eqn. No. Hertz contact stresses: a) Spherical surfaces: When two solid spheres are pressed together with a force, the radius of the area of contact Fig. 1.8(a)) When a solid sphere of diameter d; and a plane surface are pressed together with a force, the radius of the area of contact When a solid sphere of diameter d; is pressed against an internal spherical surface of diameter ds, the radius of the area of contact The maximum pressure at the centre of contact area b) Cylindrical surfaces: When two cylinders are pressed together the half width of the rectangular area of contact (Fig. 1.806) = [SF Cae + 1/82))3 =e yas + 17a) LiKe \ a= [2Fa =P O/E) + 1/E)]5 8 (a) neg 1 a= [2h = YAEL + ven! “dia = 17) 1 an Pos = 55 L136) where a is the radius of the contact area 1 _ [26 = 0 /Es + 1/E2)]? “|aL (i/di + 1/d) 1.14 where L is the length of the contacting surfaces Fig. 1.8(a): Pressure distribution between two Spheres Fig. 1.8(b): Pressure distribution between two CylindersSees Analysis 9 Particular Equation Eqn. No. a i When a cylinder of diameter d; is pressed p= [eae ie se 1.14(b) ‘azsinst a plane surface, the half width of the _ (dy) scctangular area of contact P (1p )(/E) +1. 3 When a cylinder of diameter d, is pressed b= eee 1.146) ‘sezinst an internal cylinder surface of o (dy — Vide Gemscter dy the half width of the rectangular =a of contact ‘Tae maximum pressure at the centre of Alene L.14(d) ouatact area Thermal stresses: ‘Thermal expansion ‘he total length at a temperature 1, K(°C) ‘Shes set up in the bar due to change in the ‘emperature Columns: ‘Saaler’s column formula for the critical load where L is the length of the column, mm m=constant depending on the condition of the restraint of column ends (coefficient of end conditions) (Fig. 1.9) = 0.25 for one fixed end and one free end = 1.00 for both ends free, i.e. both ends are guided or hinged =4 for both ends fixed rigidly = | to 4 for both ends flat abl where b is the half width of the rectangular area of contact 6; = alo(t — 10) 1.15(a) where Ly is the length of the bar at the initial tem- perature fo, K(°C) (t= to) = change in temp, K. (°C) L= Lol +a(t-t)] 1.15(b) o = Eatt— 1) 1.15(¢) meEl _meEAR _ nEA ao Te 1.16(a) FOF F F ‘é T ' ' i \ ! | 4 tino {In=1 PIna2 roa ““e (a) (b) () (a) (e) Fig. 1.9: End conditions of columns10 Stress Analysis Particular Equation Eqn. No. Parabolic column formula to determine the FZ Ady [i-= Site ee 1.16(b) ctitical load Straightline column formula to determine the | Fer = A (op ~ ct) 1.16(6) critical load ‘ where C = (20%yp/3) JOyp/3nE = a constant . ' : F o Rankine formula to determine the induced z [1+ acer] 1.16(4) stress in a column where F is the external force on the column, N(kgf) ais the constant in Rankine formula from Table 1.2 Ritter’s formula, which is a modification of oc= f [! + (L/k 1.16(e) the Gordon-Rankine formula, for determining the induced stress, «~. in a short column Eccentrically loaded columns (Fig, 1.9(€)) To determine the maximum combined stress | or =4l(0 + UP Se + r+ | 1.16(f) by Ritter’s formula where e is the distance between the load and the centroid and cis the distance from the centre of gravity to the outer most fiber References [1] Singer, F. L., “Strength of Materials”, Happer and Rom, New York, Evanston and London and John Weatherhill, Inc., Tokyo, 1962. [2] Morley, A., “Strength of Materials”, Longmans, Green and Co. Ltd., London, 1953. [3] Spots, M. F., “Design of Machine Elements”, 3rd edition, Prentice Hall, Inc., Maruzen Co. Ltd. [4] Shigley, J. E., “Machine Design”, 9" edition, McGraw Hill Education Private Ltd., New Delhi. 2011.Stress Analysis Table 1.1 Physical constants of some common materials Modulus of Modnins ot Tan's. | Dense, Material Elasticity, E x 10-* | rigidity, G x 10> : MN/m? (kgf/mm?) | MN/m? (kgf/mm?) | T3is# kein Aluminium (alloys) 71.0 (7.24) 26.2 (2.67) | 0.334 2730 Beryllium 287.1(29.28) - = 1820 Beryllium copper 124.2(12.66) 48.3 (4.92) | 0.285 8230 Brass 95.1 (9.70) 34.3 (3.50) | 030-040 8450 Bronze 109.0(11.10) F 4 8730 Carbon steel . 202.0(20.60) 78.5 (8.00) | 0.292 7820 Cast Iron, gray 100.0(10.20) 41.4 (4.22) | 0211 7200 Copper 120.6(12.30) 38.3 (3.90) | 0.260 8960 Inconel 214,021.80) 76.0 (7.75) | 0.290 8960 Lead 15.7 (1.60) 75 (0.76) | 0.450 11340 Megnesium 44.8 (4.57) 16.6 (1.69) | 0.350 1800 Molybdenum 331.0(33.75) 117.2(11.9) | 0.307 10200 Monel metal 179.3(18.28) 65.6 (6.68) | 0.320 8830 Nickel steel 196.1(20.00) 75.6 (7.80) | 0.291 7750 Phosphor bronze 111,011.32) 414 (422) | 0349 8160 Stainless steel (18-8) 190.3(19.40) 73.1 (7.45) | 0.305 7750 Titanium 103.5(10.55) | a 4480 ‘Tungsten 437.3(41.53) 173.617.70) | 0.170 19300 Zirconium 68.4 (6.97) , ol 6500 Table 1.2 The Values of Constant ‘a’ in equation 1.16(d) i Ne ee ES Both ends | Both ends | One end round, round | _ fixed one fixed Steel a | om ~~ Cast Iron om sw im Wrought Iron ata same aidStress Analysis 12 3 7 bien ® p-lo=y - Ho es pue (q+ HOY _ |, £ Pp 2 Pq + HO Pot Ha - Pa T HO ‘o zu > 4 ~ HE H 4 ~ Hd QQ - WU H9 z a fH (- H H ey : 9 z a 6870 a Z "4 ° 4 a4 1 4 o © ® © @ Vay 2 i Ee woreshs) sngnpoy 9 WO ISOC FNL Jo suipey wong opaouesig — | _ Jo 1uaWOWy woRag eat suoysag sso1Q snorin, fo saysodorg (D) €T AGEL13 5 e g a 4 ge 4 ge z fyb % Pe 2+ 2 ee wee | @oey- $ Ga-} +9 igus a Ga- oy a+a es = ae EI aod eIE8OOO= a2 en ead v (89+ 481 (q+ qe (04+ 4O9E 1 2U(2q + 999 + -99) 4G + 4) py -q=r0 > teed (0+) 19 qe raat Ad q < Bway TW = W— Xe a- WA Ing peog tose q> puma ye = WOW y=Acqoy Meo orton ie der AS AND or, A+ PTE cag | ER PNt got Nt BIN qat= eget at 5 ae ryt ty swoon oa =U (19e-&- DO +49)] = fs Ud 9 _¢; xlyt So y-= Weg oy (q+ 0g) ='y ES tol DPI ene a Ad (1g - x HI9 Lega (1g 4+ x76) Ad T gay 8 a 2 pue vend = WOW ab-=aromg aw ON = coun aed? = W630 ate gory (are eT wkigoy ron wiood dat = 'witat ow dieu *|af Fo= F/D-dh as w 8 8 BE 8 3 8 8 & g g z 8 e Sheena resses in eye bar. : STRESSES a (©) Mitigation of SE concentrationWorking Stresses Symbols Description and Units A correction factor for the type of loading B size factor c surface correction factor Fn average or mean load, N(kgf) F, variable or alternating load, N(kgf) K, theoretical stress concentration factor for normal stress (tension or bending) K theoretical stress concentration factor for shear stress K’ theoretical combined stress concentration factor Ky estimated fatigue stress concentration factor for normal stress Ky, estimated combined fatigue factor for normal stres Ky estimated fatigue stress concentration factor for shear stress Ky stress concentration factor in the tranverse direction n factor of safety q notch sensitivity factor for cyclic loading R reliability factor U internal elastic energy, mJ (mm-kgf) 6 Static deformation under the action of the weight W, mm ° Deformation under impact action, mm o static stress, MN/m? (kgf/mm?) oy bending stress, MN/m? (kgf/mm*) oa design stress, MN/m? (kgf/mm?) 2,0, | * direct stresses in x and y directions respectively, MN/m? (kgf/mm?) 1,02 maximum and minimum principal stresses respectively, MN/m? (kgf/mm?) Ta endurance limit stress of the material in reversed bending, MN/m? (kgf/mm?) Cena endurance limit stress of the material in reversed axial loading, MN/m? (kgf/mm°) op yield point stress, MN/m? (kgf/mm?) 1920 Working Stresses Symbols Description and Units on average or mean normal stress, MN/m? (kgf/mm?) Ce variable normal stress, MN/m? (kgf/mm?) ér design stress for completely reversed loads, MN/m? (kgf/mm?) Cea design stress for alternating loads, MN/m? (kgf/mm?) On ultimate stress, MN/m?(kgf/mm?) o impact stress, MN/m?(kgf/mm?) t shear stress, MN/m* (kgf/mm?) Tin endurance limit stress of the material in cyclic torsion, MN/m? (kgf/mm?) Te. average or mean shear stress, MN/m? (kgf/mm?) Te variable shear stress, MN/m? (kgf/mm?) Typ __ yield strength of the material in shear, MN/m? (kgf/mm?) v the impact stress due to torsion, MN/m? (kgf/mm?) @ static angular deflection, rad angular deflection under impact loading, rad Particular Equation Eqn. No. Stress concentration in members: ‘The maximum stresses at the discontinuity i) Fora direct stress: (Fig. 2.1(a)) Cmax = 7K, = tk, 2.1(a) ii) For bending: (Fig. 2.106) Cin = ook = MEK, = Bk, 2.106) iii) For torsion: (Fig. 2.1(c)) Tang HTK PKs = ok, 2.1(0) Fax = (Cnom)Ks Tensile Stress Fig. 2.1(b): Bending Stress Fig. 2.1(c): Shear StressEquation Eqn. No. stress induced around the hole ina | max = 7K, = x, 22 ‘of infinite width (Fig. 2.2) ‘2 plate with a hole is subjected to Orman = Kix + KyO'y = Kyo + Kyo> 23 stresses o, and cry acting at right ‘shen the combined maximum stress (super position) —_ Ky-1 ‘notch sensitivity index: gen 24 K-1 fatigue stress concentration factor | Ky = 1+9(K, - 1) 25 ‘stress combined fatigue factor for normal | K’, = 1+q(Kj—1) 26 fatigue stress concentration factor Ky = 1+ q(K, - 1) 27 ‘stress of failure: toy = according to the maximum normal o.=(7 x) (=) +3, 2.8(a) séeory or Rankine theory =}, maximum principle stress 0 0.2 04 0.6 08 Ratio a/B —> Fig. 2.2: Form Stress Factor due to hole in a plate22 Working Stresse Particular Equation Stress according to the maximum strain theory or Saint-Vanant’s theory Eqn. Ne Oxrt+ Oy Fx — Cy\* =(1- 2 = 0) - por a =(1-w(FS) 4040) (A) +3, =01-n02 2.8(b) Stress according to the maximum shear stress theory or Guest's theory o,- oy)? a, =24(F5) +8, = flo oF $4 = 1-0) 2.8(¢) Stress according to shear energy theory or the Hencky-von Mises theory Ge = (Ci - oxy +0} + 3r2,.) = Jo} +o} -o102 2.8(4) Maximum total strain energy theory or oO. = Jo? +03 - Yori 2.8(¢) Haigh’s theory Design for strength: Influence of size: ‘The elastic limit o for any thickness h 2.9(a) between 12.5 mm and 75 mm (Fig. 2.3 and P . 24) where B is the size factor a= 250 290 value of the ratio (or, /o~.) for a few materials are given in Table. 2.5 300 — 4h + (.,/2)(4h — 50) a & a ae & a9 2 oe 3 ES a a, Se g a a a 0 2 50 75 «100 125 10 20 30 40 50 60 70 80 Size of section, mm Size of section, mm Fig. 2.3: Influence of Size on Elastic Limit Fig. 2.4: Change of Elastic Limiswith Size of Section23 Equation Eqn. No. stress for a static load “ae 2.10 He RR ; where R is the reliability factor, Table. 2.7 stress oy = 1810, 241 for fatigue: ‘or fatigue stress concentration Ky ad =q(K,-1)+1 2.12(a) a where oy is the Endurance limit without discontinuity eng is the fatigue strength with discontinuity seress for completely reversed loads | oy, = Zen 2.120) RK between tensile strength and limit: Cen = (1/2. t0 5/8) 0% 2.13(a) Cen = 0.40 2.13(b) metals and alloys Cen = (1/4 10 1/3), 2.13(¢) stress endurance limit in of Tn and o, Ferns = (0.7 t0 1.0)o°en = (0.35 t0 5/8), 2.14(a) cast iron ‘ferrous metals and alloys torsion endurance limit in of Ten and oy ‘Steel Ser cast iron ‘Ser non-ferrous metals and alloys “Static plus alternating simple loads:- We. 2.5) “Die average or mean stress ‘The variable stress component Gena = (0.7 t0 1.0)oen = (0.28 to 0.4), 2.14(b) Gen-a = (0.7 t0 1.0)o%en = (0.175 to 1/3)o,2.14(C) Ten = (0.5 10 0.6) = (0.25 to 0.3)o, 2.15(a) Ten = 0.80, 2.15(b) Ten = 0.20, 2.15(c) 2.16(a) 2.16(b)2 Working Stresse Particular ‘The design stress for alternating loads where Fm = 2 F, The required cross-sectional area of the member for alternating loads The equivalent static load for a cyclic load FntFa The equivalent static load for a bending load Mm + Ma ‘The equivalent static load for a torsional load Typ Ta Fatigue Failure Equations (Fig. 2.6) Gerber’s parabolic relationship for fluctuating stress Goodman’s relation for fluctuating stress Soderberg’s relation for fluctuating stress — Fimax + Fin Equation Eqn. No. én + Fa) 2.17@) wee Fn (2) Fe oar . average or mean load alternating load Az Fat _ Fut Fo 2.17(b) Oda da Fy = Fin + (Cal ar)Fa 2.18(a) ; My = My + (0a Oar)Ma 2.18(b) | m+ (Caloa)Ta 2.18(€) Oa = eal —(m/ou)*] oF 2.19(a) eee (=) =1 Ta \Ou 2.19(b) 2.19(6) Stress, 7 —> Time, t —> Fig. 2.5: Fluctuating Stress Variable stress —» Average Stress—> Fig. 2.6: Fatigue Failure EquationsParticular Equation Eqn. No. ‘Goodman's relation for fluctuating torsional | t. = ral = 2) or 284 Smecbw. ten —. ta) Tent Faon Fe Seecberg’s relation for fluctuating tosional | T= Ten G ~ 2) op Hy tm at 21m) ess nN Typ Tees Come ‘The maximum cyclic stress in terms ef the endurance limit: Accoeding to Goodman relation Ones = 22 +0 ( E ca) 2.200@) _Aeconding to Soderberg relation Cmax = es: +om ( = ga) 2.206) vp ‘ee case of cyclic torsion the maximum Pee ad ( » 2) 2.20(¢) ‘according to Soderberg relation. - Tp the correction factors into xcount: “Phe Gooxman'’s relationship = fr ductile materials 2.21(a) 2 Kia ‘Ser brittle materials tee 2.21(b) “Dee Soderberg relationship 7 Kiyoa | om _ 1 ‘= fer ductile materials pert ee as 2.21(0) ; ‘ Kyoa |p Im _ 1 © Sor brittle materials Tere Nan 2.2K) FE aa KsjTa_ | T™m _ 1 © for ductile materials in shear ee ee 2.21(e) where A = 1.0 for reversed bending, =0.7 to 1.0 for reversed axial loading 5 to 0.6 for reversed torsional loading B is the size correction factor (Eqn. 2.9(b)) C is the surface correction factor (Table 2.2) n is the factor of safety (Table II-1)26 Working: Particular Equation Eqn. The equivalent maximum shear and normal stresses: meee: : a op) Kiso The equivalent normal stress Cen = Tmt (2) am ‘The equivalent shear stres rh ara Oe equi shear stress = tm +(2 | ac ‘The equivalent maximum shear stress ‘The equivalent maximum normal stress to be used when designing with brittle materials O eq—n(Max) = ~f Inertia stresses and Centrifugal loads: ‘The general expression for the centrifugal force where, v= velocity, m/s = radius of curvature W =weight, Nckef) g=acceleration due to ‘The centrifugal force per unit volume In the case of a coupling rod (Fig. 2.7), (i) The centrifugal force (ii) Bending component of the centrifugal force of the path of the motion of the mass, m. gravity, m/s?. where w = the specific weight of the material, N/mm) (kgf/mm?) eS aa gR where, /r= height of coupling rod, mm 1= thickness of coupling rod, mm and L=length of coupling rod, mm Fou we ito eS ce + 22k gR gR where, a = crank angle, degrees W =total weight of the coupling rod, N(kgf).Stresses 27 Particular Equation Eqn. No. 2 “Ge The maximum bending component of | F,,(max) =~ Ent = ae 2.24(e) ‘Ge centrifugal force (when a = 0°, i.e. at b) 8 & o 5 1 we laa The maximum bending moment (when | Mpax = Fos(max)L = = Rhtl? = — a 2.24(f) ==. ic. ab) ! ge) The axial component of the centrifugal | Foy ="“CheLsina = eins 2.24(g) oo em we = : we The maximum axial component of the —— 2.24(h) centrifugal force (when a = 90°, i.e. ata’) Smpact Energy: eae Kimetic Energy hes 2.25(a) Smpact energy of a body falling from a Ex =Wh 2.25(b) eich, h ‘The internal elastic energy U=Wh+6)= 2.25(€) wr We velocity has a random direction, then 2.25(d) ‘Be internal elastic energy Impact stress “The general equation for the impact stress U == ++ Wo' sina 28 where v; is the velocity of the moving body, mm/sec g is the acceleration due to gravity, mm/s? of = a(l + VIF DHT) = Wa + VIFIREATWD) ‘The general equation for the deformation sender impact action ‘The impact stress due to bending 6’ = (1+ V+ 2h70) of, = oy(1 + 1+ 2h]y) 2.26(a) 2.26(b) 2.26(c) Fig. 2.7: Locomotive Coupling Rod28 Working Stresses Particular Equation Eqn. No. Deflection under impact action due to bending | y’ = y(1 + yi + 2h/y) 2.26(d) The impact stress due to torsion v=1(1+ VI+2h/70) 2.26(e) ‘The angular deformation due to impact 6 = 1 + \T+2h7r8) 2.26(f) Done estan) where is the moment arm of the load W Impact stress due to sudden load (o’ = 20), (1, = 20) and (7 = 27) ——2.26(g) Deformation under impact action due to (6 = 26), (y’ = 2y) and (@ = 24) 2.26(h) sudden load e 2 F L+am ‘When a body having a wieght W strikes "= Gabo? 2.26(i) another body that has a wieght W’ according Cee to the laws of collision of two perfectly where m = W’/W inelastic bodies, the impact energy Wh is and b are coefficients (Table 2.8) reduced nWh. The value of n may be found by the formula Resilience: ; The resilience of a body U = 5F6 2.21(a) where F = average applied force = W when load is applied without impact Wo’ _ Wo’ =, when load is applied with impact (a) Axial load (b) Bending load Fig. 2.8: Impact StressesWorking Stresses 29 Particular Equation Eqn. No. ; Vv Resilience in tension or compression vase 2.27(b) where V = AL, Volume of the body, mm* K} | (k) PAL Resilience ii i —|(-) —— i ence in bending |; = (-) : 2.21(¢) where (k/c)* = (1/3), for rectangular sections = (1/4), for circular sections K; is the constant in the deflection equation (y = FL*/KE) corresponding to the type of loading Ke is the constant in the maximum moment equation (M = FL/Ka) corresponding to the type of loading k is the radius of gyration Resilience in shear ev 221d) “te Resilience in torsion u (=) = 2.271) where k, is the polar radius of gyration _ References Siegel M.J., Malev V. L., Hartman J. B., “Mechnaical Design of Machines”, 4th edition, Interna- tional Text Book Company, 1965. ©) Vallance A., Doughtie V. L., “Design of Machine Members”, 3rd edition, McGraw-Hill Book Co., 1951. 1S) Spouts M. E., “Design of Machine Elements”, 3rd edition, Prentice Hall, Inc., Maruzen Co. Ltd. ©) Black P. H., “Machine Deisgn”, 3rd edition, McGraaw Hill Book Company, Inc. G) Faires V. M. esign of Machine Elements”, 2nd Edition, The Macmillan Company, 1941. ©) Shigley J. E., “Machine Design”, McGraw Hill Book Company, Inc. 7) Hyland P. H., Kommers, J. B., “Machine Design”, McGraw Hill Book Company, 1943. ©) Hall A. S., HoloWenko, A. R., Laughlin H. G., “Schaum's Outline of Theory and Problems of Machine Design”, Schaum Publishing Co., 1961. ©) Slaymaker R. R., “Mechanical Design and Analysis”, John Wiley and Son, Inc., 1958. 0) Roark R. J., “Formulas for stress and strain”, McGraw Hill Book Company 1954.Working Stress Table 2.1 Stress Concentration Factors ‘Type of form irregularity or | Manner of | _ Equation for the stress Experimental stress riser loading concentration factor value of ' the factor K, or Nor Ky 2 . 1. A Round hole in a plate of Tension | K, = 3f2+(Z) +3(S)] K=3 infinite width (Fig. 2.9) mi 2. Round filled hole Tension K,=25 3. The pin in a hole transmits Tension Baas the load K=05 4, For a small V-notch at the Tension K,=1+2vhjr edge of the place Fig. 2.10 where h = depth of the notch r= radius at the notch corner 5. An Elliptical hole in a plate | Tension K=1428 with major axis normal to the ° load (Fig. 2.11) 6. An Elliptical hole ina plate, | Tension + = the major axis along the load b=semi major axis and c semi minor axis Fig. 2.9: Stress concentration Sor a plate with hole in tension ty, I orl sat 4 Teles a) AR “ any ili Fig. 2.10: Form-Factor ratio due to notches of various shapes31 ‘Tepe of form irregularity or | Manner of ‘Equation for the stress Experimental stress riser loading concentration factor value of the factor K, or N or Kiy ways with b = d/4 and Profile key way Shear K, = 1.68 )Sied runner Shear Ky = 144 thread TDF threads Tension Kyy = 2.5 103.75 Whaworth Tension K,y = 151030 and shrink fit Plain member K, = 195 ‘(Geooved member K,=134 ‘Roesting disc with hole Fer R/R, 0 K,=2 ‘Thin Ring K.=1 4C-1 , 0.615 ‘BiScal spring Shear pee a where C is the spring index ‘Cease hook K, = 1.56 Gear teeth . 1,020 7, 10:40 A the root fillet of 144 Bending x,=022+[4] [4] ‘imvolute a 1,715 p 4, 7088 At the root fillet of 20° Bending k= 0.18[4] ee ‘molute - fa |e (Carved beam Bending | K, 10+8[ 5] ae where B = 1.05 for circular or elliptical sections ).5 for other sections c is distance of the extreme fiber from the centroidal axis r is the radius of curvatureWorking Stres: Table 2.2 The average values of the surface correction factor C Ultimate | C for Machine C for Ultimate C for Machine Cfor stress. surface hot rolled stress surface hot rolled o,MN/m? 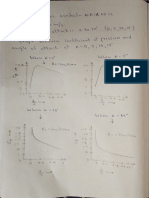| (Cold drawn) surface o.MN/m* | (Cold drawn) surface (Kef/mm*) (Kgf/mm?*) 410 (42) 0.91 0.72 760 (77) 0.84 0.52 480 (49) 0.90 0.68 820 (84) 0.82 0.48 550 (56) 0.88 0.62 1030 (105) 0.78 0.38 620 (63) 0.86 0.58 1370 (140) 0.72 0.30 690 (70) 0.85 0.55 - - = Table 2.3 Chart for Guidance in Selecting Stress-Concentration Factors for Various Types of Loading and Materials Brittle material Ductile material Foaling. | _Nerial Shear Normal Shear Static K, K, Neglect Neglect Cyclic K, K, ie Ky Table 2.4 Index of Sensitivity for Repeated Stresses Average Index of Sensitivity, q Heat treated | Heat treated and drawn | and drawn Material a ea nt 920K at 750K (650°C) (480°C) ‘Armco iron, 0.02% C ~. | 0.15-0.20 Carbon steel : 0.10%C «. | 0.05-0.10 0.20%C (also cast steel) a 0.10 2 3 0.30%C . 0.18 0.35 0.45 0.50%C bs 0.26 0.40 0.50 0.85%C 2 a 0.45 0.57 Spring steel, 0.56%C, 2.3 Si, rolled 2 . 0.38 2 SAE 3140, 0.37% C; 0.6% Cr;13%Ni 0.25 0.45 s Cr—Ni steel, 0.8% Cr; 3.5% Ni : 0.25 0.70 Stainless steel, 0.3% C; 8.3% Cr; 19.7% Ni .. 0.16 Cast iron | 00.05 Copper, electrolitic a 0.07 Duraluminium =. | 0.05-0.13