23

Kinematics

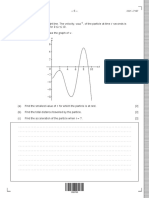
Exp. (c) 41. A point P moves

counter-clockwise
For a particle in uniform circular motion, B
direction on a circular
Px.y
path as shown in the
P(R, 0) figure. The movement 20
A is such thatit
a X
of P
sweeps out a length
S =t+5, where s is in
metre andt is in second. The radius of the
path is 20 m. The acceleration of P when
a towards centre of circle
R t 2 sis nearly [AIEEE 2010]
centripetal acceleration] (a) 13 ms- b) 12 msz
(c) 7.2 ms2 (d) 14 ms
a -cosei-sinej)
Exp. ()
of a =-cosei -sine i Given, S =t +5
R R

40. A small particle of mass m is projected at an

Speed, v ==3t2
dt
angie with the x-axis with an intial velocityv
in the xy plane as showm in the figure. At a time and rate of change of speed, a, = = 6
dt
t Sin6
0 ,the angular momentum of the Tangential acceleration att =2s,
8
particle is AIEEE 20101 a =
6x2 12 ms2

and at t =2 S, V = 3(2 = 12 ms

Vo Centripetal acceleration
v144
R 20
ns
Net acceleration = a +a =14 ms2

42. Aparticle has an initial velocity 3i+4 and an

(a)-mgv cosej b) mgv,tcosek acceleration of 0.4i+0.3j. Its speed after 10 s
c)mgv cosek(d)mgv,
2 cosei is
(a) 10 units (b) 7/2 units
AIEEE 2009
(c) 7 units (d) 8.5 units
Exp. (e)
Angular momentum of the particle is Exp. (b)
L m (rxv) Given, u=3i+ 4j:a =04i+0.3
V =U+aat
=L=mcos8t i +( sinet -gi 3i+ 4j+(0.4i+03))10
x [Vocosei+V,sine gt) j] 3i+4+ 4i+3
= 7i +7
mvgcoset So, speed is equal to magnitude of velocity
= 73+72 =7/2 units
-mgtcose k