Professional Documents
Culture Documents
0 ratings0% found this document useful (0 votes)
54 viewsMathematics in The Modern World (Notes) PDF
Mathematics in The Modern World (Notes) PDF
Uploaded by
RamramVasquezThis document provides an overview of mathematics from different perspectives:
1. It discusses the historical, conceptual, philosophical, and practical perspectives of mathematics. Mathematics originated to address practical needs and has evolved over time.
2. Key mathematical concepts are explored, including quantity, structure, space, change, and foundations. Mathematical concepts are interrelated.
3. The document introduces different types of transformations including isometries, dilations, translations, rotations, reflections, and glide reflections. Symmetry patterns in nature are also examined.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You might also like
- Chapter 9 - The Verdict On Groupthink Case StudyDocument2 pagesChapter 9 - The Verdict On Groupthink Case StudyAdelson Arado100% (2)
- Jigsaw AssessmentDocument8 pagesJigsaw AssessmentNur Syafiqah Abu BakarNo ratings yet
- Calculus B: The First Professional IntroductionDocument15 pagesCalculus B: The First Professional IntroductionOgulnabat TashlievaNo ratings yet
- Mathematical Language and Symbols: Math 01 - Mathematics in The Modern WorldDocument30 pagesMathematical Language and Symbols: Math 01 - Mathematics in The Modern WorldMilk BrotherNo ratings yet
- Determining The Equation of Quadratic Functions Given Its GraphDocument3 pagesDetermining The Equation of Quadratic Functions Given Its GraphElla Jane E. BautistaNo ratings yet
- Nature of MathematicsDocument4 pagesNature of MathematicsAyu PhCareNo ratings yet
- Exam Formula Sheet (1) PhysicsDocument3 pagesExam Formula Sheet (1) PhysicsIncksNo ratings yet
- Grad+Div+Curl Coordinates Part3Document3 pagesGrad+Div+Curl Coordinates Part3christopher23No ratings yet
- On Reduction of Relative Velocity With Relation To Space-Time Co-OrdinateDocument5 pagesOn Reduction of Relative Velocity With Relation To Space-Time Co-OrdinateTathaNo ratings yet
- Mat061 Chapter 2Document40 pagesMat061 Chapter 2Enaira100% (1)
- Partial DerivativesDocument31 pagesPartial DerivativesaliNo ratings yet
- Unit-2 Vector CalculusDocument86 pagesUnit-2 Vector CalculusRitesh MukhNo ratings yet
- PRECALCULUS Quarter 1 Module 3Document6 pagesPRECALCULUS Quarter 1 Module 3alohajilljarabe123No ratings yet
- Math 01 Lecture 2.1Document30 pagesMath 01 Lecture 2.12C1 - YABES, JenniferNo ratings yet
- Module 6 Homogeneous Differential Equation With Constants CoefficientsDocument3 pagesModule 6 Homogeneous Differential Equation With Constants CoefficientsTherese SibayanNo ratings yet
- Learning-Plan-GENERAL MATHEMATICS 11 Lesson 11Document4 pagesLearning-Plan-GENERAL MATHEMATICS 11 Lesson 11Ivy-Jane Natanauan UmandapNo ratings yet
- Tutorial Unit 2Document3 pagesTutorial Unit 2Mukesh KumarNo ratings yet
- BasicCalQ3W2 SLMDocument10 pagesBasicCalQ3W2 SLMNasos 2No ratings yet
- Properties of Complex Numbers (Contd) : NPTEL - Physics - Mathematical Physics - 1Document8 pagesProperties of Complex Numbers (Contd) : NPTEL - Physics - Mathematical Physics - 1vkphyNo ratings yet
- Mathematics 9 Quarter 1 Week 8: NAME: - GR & SEC: - CompetencyDocument11 pagesMathematics 9 Quarter 1 Week 8: NAME: - GR & SEC: - CompetencyPARMAN, REGINE MAYE C.No ratings yet
- M31 Limits Week 1 NotesDocument15 pagesM31 Limits Week 1 NotesYolanda ChangNo ratings yet
- Pre Calculus HandoutsDocument14 pagesPre Calculus HandoutsVince Leo Panoncillon GonzalesNo ratings yet
- Genmathweek 2Document8 pagesGenmathweek 2Ricky LumantaNo ratings yet
- Session 1Document26 pagesSession 1Hao ChenNo ratings yet
- PYL101 QM Lecture 5Document11 pagesPYL101 QM Lecture 5mukeshNo ratings yet
- ME223-Lecture 26 and 27 Thick CylindersDocument19 pagesME223-Lecture 26 and 27 Thick CylindersArushiNo ratings yet
- Null Ticket - Calc-3Document2 pagesNull Ticket - Calc-35gdkrhrjnxNo ratings yet
- Calculus II 2021-2022 S2 MidtermDocument6 pagesCalculus II 2021-2022 S2 MidtermhoqueipatinsportugalNo ratings yet
- Learning-Plan-GENERAL MATHEMATICS 11 Lesson 9 and 10Document4 pagesLearning-Plan-GENERAL MATHEMATICS 11 Lesson 9 and 10Ivy-Jane Natanauan UmandapNo ratings yet
- Chapter 6Document5 pagesChapter 6Muntazir MehdiNo ratings yet
- Questão 01 NOTAÇÃO INDICIALDocument5 pagesQuestão 01 NOTAÇÃO INDICIALAnderson SilvaNo ratings yet
- Chapter 2 Mat455Document36 pagesChapter 2 Mat455Ajaq 98No ratings yet
- Jee Advanced 2022 Paper 2Document13 pagesJee Advanced 2022 Paper 2mickelsonniklaus995No ratings yet
- Lec2 PDFDocument3 pagesLec2 PDFAbhisek RoyNo ratings yet
- Advanced AlgebraDocument10 pagesAdvanced AlgebraMANGULABNAN, REY JOSEPH, E.No ratings yet
- Chapter 1 - Complex NumbersDocument19 pagesChapter 1 - Complex NumbersRyan A. RamosNo ratings yet
- Vector Calculus Add OnDocument86 pagesVector Calculus Add Onabiramijeyaseelan05No ratings yet
- Finite Difference Methods For Two-Point Boundary Value Prob-LemsDocument3 pagesFinite Difference Methods For Two-Point Boundary Value Prob-LemsasasdNo ratings yet
- Lecture-5-6 Moment, Skewness and KurtosisDocument5 pagesLecture-5-6 Moment, Skewness and KurtosisNafiul Alam SnigdhoNo ratings yet
- Unit 1 - Topic 2Document24 pagesUnit 1 - Topic 2lorenzjohn777No ratings yet
- Class 10 Math Formulas (C.B.S.E)Document6 pagesClass 10 Math Formulas (C.B.S.E)Vaibhav RachapudiNo ratings yet
- Analytic Geometry (11-21)Document4 pagesAnalytic Geometry (11-21)blueberrytimeNo ratings yet
- Quadratic Functions: B. Learning Outcome Performance StandardDocument7 pagesQuadratic Functions: B. Learning Outcome Performance StandardHenry Kahal Orio Jr.No ratings yet
- Notes Zeghib1Document15 pagesNotes Zeghib1JordandomNo ratings yet
- Calculus Module 3Document22 pagesCalculus Module 3Karl AngcananNo ratings yet
- LIVE NOTES DIFFERENTIAL CALCULUS FOR SL Students of AA and AIDocument26 pagesLIVE NOTES DIFFERENTIAL CALCULUS FOR SL Students of AA and AIsriramaniyerNo ratings yet
- Sph4u Note Energy Analysis + Planetary MotionDocument3 pagesSph4u Note Energy Analysis + Planetary MotionDavid HilbergNo ratings yet
- 1 2 J P Total 1 2 I X P Total: Estimation of One Missing Observation in LSDDocument3 pages1 2 J P Total 1 2 I X P Total: Estimation of One Missing Observation in LSDSerajum Monira MouriNo ratings yet
- 3a. Plane Stress - Plane Strain 2 StuDocument36 pages3a. Plane Stress - Plane Strain 2 Stushivam ojhaNo ratings yet
- Solution Manual Chapter 7Document14 pagesSolution Manual Chapter 7Hazlina ZaiyunanNo ratings yet
- NSEP 2022 Question Paper With SolutionsDocument46 pagesNSEP 2022 Question Paper With SolutionsATRIJA PALNo ratings yet
- Calculus II 2018-2019 S2 Midterm Test 2Document3 pagesCalculus II 2018-2019 S2 Midterm Test 2Frank WanNo ratings yet
- IT5409 - Ch6-Motion Detection and Tracking-Eng v1.0Document58 pagesIT5409 - Ch6-Motion Detection and Tracking-Eng v1.0Bui Minh DucNo ratings yet
- Formula Sheet PhysicsDocument2 pagesFormula Sheet PhysicsThar Lon Lin HtetNo ratings yet
- BYJU'S Home Learning Program: Daily Practice ProblemsDocument5 pagesBYJU'S Home Learning Program: Daily Practice ProblemsJagdamba prasad yadavNo ratings yet
- Module in General Mathematics: OBJECTIVE: Determines The Intercepts, Zeroes, and Asymptotes of An Exponential FunctionDocument20 pagesModule in General Mathematics: OBJECTIVE: Determines The Intercepts, Zeroes, and Asymptotes of An Exponential FunctionMarco SeəsonNo ratings yet
- 1st DLP-MATHEMATICS8-OCTOBER 20, 2023Document5 pages1st DLP-MATHEMATICS8-OCTOBER 20, 2023karlajean bongatoNo ratings yet
- SC Grade 9 Unit 5 - MensurationDocument21 pagesSC Grade 9 Unit 5 - MensurationJitender sehrawatNo ratings yet
- Math IA On CalculusDocument9 pagesMath IA On CalculusZehraNo ratings yet
- Application of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsFrom EverandApplication of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- Inverse Trigonometric Functions (Trigonometry) Mathematics Question BankFrom EverandInverse Trigonometric Functions (Trigonometry) Mathematics Question BankNo ratings yet
- Applications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankFrom EverandApplications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankNo ratings yet
- Navigating Digital Ethiopia A Look Into EthiopiaDocument4 pagesNavigating Digital Ethiopia A Look Into Ethiopiabekyab53No ratings yet
- Binary Lesson WorksheetsDocument8 pagesBinary Lesson WorksheetsmyschoolonthegoNo ratings yet
- Tense: Atle Grønn and Arnim Von StechowDocument29 pagesTense: Atle Grønn and Arnim Von StechowCamila SilvestreNo ratings yet
- Forklift Vocabulary 2Document2 pagesForklift Vocabulary 2Alexandra KogukharNo ratings yet
- The Bug Shop: Ben Nagy & The GrugqDocument47 pagesThe Bug Shop: Ben Nagy & The Grugqtimtom123No ratings yet
- Spatial Variation in Evapotranspiration and The Influence of Land Use On Catchment HydrologyDocument25 pagesSpatial Variation in Evapotranspiration and The Influence of Land Use On Catchment HydrologyDaniel PabonNo ratings yet
- Quiz CworldDocument1 pageQuiz Cworldforda ytpremiumNo ratings yet
- Detail Drawing of Pump and Blower Room ITBPDocument1 pageDetail Drawing of Pump and Blower Room ITBPAminur RahmanNo ratings yet
- Instant Download Mri in Practice 4th Edition Ebook PDF PDF FREEDocument15 pagesInstant Download Mri in Practice 4th Edition Ebook PDF PDF FREEronald.dancy562100% (52)
- Sustainable Energy, Grids and NetworksDocument8 pagesSustainable Energy, Grids and NetworksРоман БуйнийNo ratings yet
- Mental Health & Wellbeing For Children & Young People - Part TwoDocument24 pagesMental Health & Wellbeing For Children & Young People - Part Twomariya khanNo ratings yet
- Chapter 3: Fundamentals of CrystallographyDocument51 pagesChapter 3: Fundamentals of CrystallographyAli ZbayelNo ratings yet
- The Role of Public Relations in Organiza Tional Crisis ManagementDocument2 pagesThe Role of Public Relations in Organiza Tional Crisis ManagementSalahudeen GbolahanNo ratings yet
- Chapter 1 MergedDocument65 pagesChapter 1 MergedAdi SaputraNo ratings yet
- The Impact of Desktop Publishing and Secretaries Performance ReviewedDocument11 pagesThe Impact of Desktop Publishing and Secretaries Performance ReviewedwaheedbasitadebayoNo ratings yet
- Alpha RT PDFDocument8 pagesAlpha RT PDFHugo GranadosNo ratings yet
- Airbus 29 A300 A310 HydraulicsDocument186 pagesAirbus 29 A300 A310 HydraulicsElijah Paul Merto86% (7)
- Data Sheet Ulf 600 Pro2Document3 pagesData Sheet Ulf 600 Pro2Salman ZaheerNo ratings yet
- Multi-Stage Reciprocating CompressorsDocument14 pagesMulti-Stage Reciprocating CompressorsSajad FalahNo ratings yet
- Grade 5 - Arts ActivitiesDocument7 pagesGrade 5 - Arts ActivitiesMarcus Sayson DabonNo ratings yet
- LogDocument6 pagesLogDaniel SousaNo ratings yet
- The 7 Laws of Clearing Ca Final 9350712539Document83 pagesThe 7 Laws of Clearing Ca Final 9350712539sanjay sNo ratings yet
- Good Things Come To Those Who Wait, But Only Those Things Left by Those Who Hustle' by Abraham LincolnDocument12 pagesGood Things Come To Those Who Wait, But Only Those Things Left by Those Who Hustle' by Abraham Lincolnsiva_mmNo ratings yet
- Cek Virus CMDDocument3 pagesCek Virus CMDMohamad Razif Abd RazakNo ratings yet
- RoberDocument2 pagesRoberVernet LactNo ratings yet
- Resilient Marketing Ebook FDocument20 pagesResilient Marketing Ebook Fmaneesh mittalNo ratings yet
- Baeng 102Document7 pagesBaeng 102Chinni ChinniNo ratings yet
- Acp Module 2.1Document36 pagesAcp Module 2.1Ashly Sacdalan ViolandaNo ratings yet
Mathematics in The Modern World (Notes) PDF
Mathematics in The Modern World (Notes) PDF
Uploaded by
RamramVasquez0 ratings0% found this document useful (0 votes)
54 views4 pagesThis document provides an overview of mathematics from different perspectives:
1. It discusses the historical, conceptual, philosophical, and practical perspectives of mathematics. Mathematics originated to address practical needs and has evolved over time.
2. Key mathematical concepts are explored, including quantity, structure, space, change, and foundations. Mathematical concepts are interrelated.
3. The document introduces different types of transformations including isometries, dilations, translations, rotations, reflections, and glide reflections. Symmetry patterns in nature are also examined.
Original Description:
Original Title
Mathematics in the Modern World (Notes).pdf
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThis document provides an overview of mathematics from different perspectives:
1. It discusses the historical, conceptual, philosophical, and practical perspectives of mathematics. Mathematics originated to address practical needs and has evolved over time.
2. Key mathematical concepts are explored, including quantity, structure, space, change, and foundations. Mathematical concepts are interrelated.
3. The document introduces different types of transformations including isometries, dilations, translations, rotations, reflections, and glide reflections. Symmetry patterns in nature are also examined.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
0 ratings0% found this document useful (0 votes)
54 views4 pagesMathematics in The Modern World (Notes) PDF
Mathematics in The Modern World (Notes) PDF
Uploaded by
RamramVasquezThis document provides an overview of mathematics from different perspectives:
1. It discusses the historical, conceptual, philosophical, and practical perspectives of mathematics. Mathematics originated to address practical needs and has evolved over time.
2. Key mathematical concepts are explored, including quantity, structure, space, change, and foundations. Mathematical concepts are interrelated.
3. The document introduces different types of transformations including isometries, dilations, translations, rotations, reflections, and glide reflections. Symmetry patterns in nature are also examined.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
You are on page 1of 4
CHAPTER I: - self-evident statements ▪ Isometry – preserver distance
- systematic developments between any two points
A. What is Mathematics? Dilation – every point is moved
“Mathematics stands on the ▪
from its original position along the
Historical Perspective establishments of reality and truth.” line connecting the origin and the
Mathematics – “mathemata” – entirety Conceptual Perspective point.
of knowledge or subject of instruction or ▪ Quantity – various operations with 𝑑((𝑥, 𝑦)) = 𝑘(𝑥, 𝑦)
study. number mathematic sets. 𝑘≠0
▪ Structure – interconnections of thee k is the scale of dilation
Numeration – first embodiment of 1. 𝑃𝑜𝑖𝑛𝑡𝑠 = (2,1)
mathematics. properties of various mathematical
𝑑 (𝑥, 𝑦) = 𝑘 (𝑥, 𝑦)
objects. (Linear Algebra, Abstract
➢ Hunters > Farmers > Larger community 𝑑 (2,1) = 2 (2,1)
Algebra) 𝑑 (2,1) = (2 (2), 2 (1))
w/ Government
▪ Space – introduction and non- 𝑑 (2,1) = (4,2)
“Mathematics came into existence for a introduction of measurements and 2. 𝑃𝑜𝑖𝑛𝑡𝑠 = (2,1)
need to address their practical quantitative coordinates (Geometry, Trigonometry) 𝑑 (𝑥, 𝑦) = −1/2 (𝑥, 𝑦)
𝑑 (2,1) = −1/2 (2,1)
necessities.” ▪ Change – existence, treatments and 𝑑 (2,1) = (−1/2 (2), −1/2 (1))
Philosophical Perspective organization of infinitesimals observe in 1
finite dimensions (Calculus) 𝑑 (2,1) = (−1, − )
▪ Intuitionism 2
- Not inherent in the physical world, but ▪ Foundation – theoretical base of Symmetry
came from the human mind. Mind entirety of math (Set theory, Math o Translation - shifts figure from one
possess forms of space and time, called Logic) place to another along the direction
“Mathematical concepts are interlocking ℎ
modes of perception or intuition. of a vector [𝑘 ]
(Immanuel Kant) and overlapping blocks.” 1. 𝑃𝑜𝑖𝑛𝑡𝑠 = (−4, −2) ℎ = 1 𝑘 = 3
- Every mathematical construction are 𝑡((𝑥, 𝑦)) = (𝑥 + ℎ, 𝑦 + 𝑘)
Practical Perspective 𝑡 ((−4, −2)) = (−4 + 1, −2 + 3)
mental construction. (Luitzen Egbertus
▪ Home 𝑡 ((−4, −2)) = (−3,1)
Jan Brouwer)
▪ School o Rotation - if it moves a point along
- rejects the idea of non-constructive
▪ Work a circular arc at a prescribed angle
existence proof
▪ Community with respect to a fixed point Q. Given
- Law of Excluded Middle and the Law
of Evolution “Mathematics is a tool to address a rotation R with angle and fixed
▪ Logicism particular problems or concerns in our point, Q, we call angle as the angle of
rotation and Q as the rotocenter.
- derivable from principles of logic; everyday living.” 1. 𝑟 = 90° − 𝑐𝑜𝑢𝑛𝑡𝑒𝑟𝑐𝑙𝑜𝑐𝑘𝑤𝑖𝑠𝑒
activity to be developed 𝑟𝑜𝑡𝑎𝑡𝑖𝑜𝑛 𝑓𝑟𝑜𝑚 𝑜𝑟𝑖𝑔𝑖𝑛
- Mathematics is logic in disguise 𝑃𝑜𝑖𝑛𝑡 = (−4, −3)
- Primitive concepts B. Patterns and Numbers in 𝑟 (−4, −3) = (−(3), −4)
o Strong Logic – truth in a particular Nature and in World 𝑟 (−4, −3) = (3, −4)
branch of mathematics. 2. 𝑟 = 180° 𝑐𝑜𝑢𝑛𝑡𝑒𝑟𝑐𝑙𝑜𝑐𝑘𝑤𝑖𝑠𝑒
𝑟 (𝑥, 𝑦) = (−𝑥, −𝑦)
o Weak Logic – truth only within the Transformations – change of location; 𝑟 (5, −2) = (−(5), −(−2))
scope of a theorem. giving the points new location 𝑟 (5, −2) = (−5,2)
▪ Formalism ▪ Identity – simplest transformation o Reflection – with respect to a line
- should be developed through axiomatic 1. 𝑖 ((3,1)) = (3,1) if it moves a point to a position
systems. 2. 𝑖 ((−5,2)) = (−5,2) exactly the opposite of its original
position such that the segment o Cyclic Order – n if its only - Exactly one family of glide
joining the point and its symmetries come from a family reflections
perpendicular with the given line. rotations of angle 360°. o Type mm (Spinning Jump)
Given reflection defined by any line, o Dihedral Order – n if its only - exactly one family of
that line is called mirror axis. symmetries come from a family of translations.
1. 𝐿𝑒𝑡 𝑚 𝑏𝑒 𝑡ℎ𝑒 𝑟𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑎𝑏𝑜𝑢𝑡 𝑡ℎ𝑒 𝑙𝑖𝑛𝑒 𝑦 = rotations of angle 360°/n and a - Exactly one family of vertical
𝑥. family of reflections about n lines reflections
𝐼𝑡 𝑖𝑠 𝑔𝑖𝑣𝑒𝑛 𝑏𝑦 𝑡ℎ𝑒 𝑓𝑜𝑟𝑚𝑢𝑙𝑎
𝑚 (𝑥, 𝑦) = (𝑦, 𝑥)
meeting at angles 180°/n - Exactly one family of half-turn
𝑃𝑜𝑖𝑛𝑡 = (3,1) (180° rotation)
𝑚 (3,1) = (1,3) ▪ Border Patterns/Frieze
Patterns – if its families of ▪ Wallpaper
2. 𝐿𝑒𝑡 𝑚 𝑏𝑒 𝑡ℎ𝑒 𝑟𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑎𝑏𝑜𝑢𝑡 𝑡ℎ𝑒 𝑥 − symmetries does not contain a Patterns/Network Patterns
𝑎𝑥𝑖𝑠 fixed point but has a fixed line. – if its families of symmetries
𝑖𝑡 𝑖𝑠 𝑔𝑖𝑣𝑒𝑛 𝑏𝑦 𝑡ℎ𝑒 𝑓𝑜𝑟𝑚𝑢𝑙𝑎
𝑚(𝑥, 𝑦) = (𝑥, −𝑦) All border patterns have one does not contain a fixed point
𝑃𝑜𝑖𝑛𝑡 = (−3, −2) direction of translation vector. nor a fixed line. Structurally
𝑚 (−3, −2) = (−3, −(−2)) o Type 11 (Hop) formed by two distinct
𝑚 (−3, −2) = (−3,2) - exactly one family of translations with vectors that are
o Glide Reflection – with respect to translations. not multiples of each other.
the line if it is a reflection about the o Type 1m (Jump) o Type p1
given line followed by a translation by - exactly one family of - exactly 2 families of translations
a vector with direction parallel with translations. o Type p2
the given line (combination of - Horizontal reflection - half-turn rotations
reflection and translation). Given a o Type m1 (Sidle) o Type p3
glide reflection g defined any line, - exactly one family of o Type p4
that line is called the glide axis. translations. o Type p6
1. 𝐷𝑒𝑓𝑖𝑛𝑒 𝑡ℎ𝑒 𝑔𝑙𝑖𝑑𝑒 𝑟𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑔 𝑤𝑖𝑡ℎ 𝑦 = - Exactly one family of vertical o Type pm
−𝑥 𝑎𝑠 𝑡ℎ𝑒 𝑔𝑙𝑖𝑑𝑒 𝑎𝑥𝑖𝑠 𝑏𝑦 𝑡ℎ𝑒 𝑣𝑒𝑐𝑡𝑜𝑟 [−2/2]
𝑔 ((𝑥, 𝑦)) = (−𝑦 + ℎ, −𝑥 + 𝑘)
reflections - parallel mirror axis
𝑔 ((𝑥, 𝑦)) = (−𝑦 + (−2), −𝑥 + 2) o Type 12 (Spinning Hop) o Type pg
𝑔 ((𝑥, 𝑦)) = (−𝑦 − 2, −𝑥 + 2) - Exactly one family of translation - Parallel glide axis
𝑇ℎ𝑒 𝑣𝑒𝑟𝑡𝑖𝑐𝑒𝑠 𝑎𝑟𝑒 𝑎𝑡 𝐴 (−1, −2), 𝐵 (−2,0), 𝐶 (−3, −1) - Exactly one family of half-turn o Type cm
𝑔 ((−1, −2)) = (−(−2) − 2, −(1) + 2) (180° rotation) - family of reflections and glide
= (2 − 2, 1 + 2)
o Type 1g (Step) reflections
= (0,3)
𝑔 ((−2,0)) = (−(0) − 2, −(−2) + 2) - Exactly one family of translation o Type Pmm
= (−2, 2 + 2) - Exactly one family of glide - exactly 2 families of reflections
= (−2, 4) reflections - one family has axis
𝑔 ((−3, −1)) = (−(−1) − 2, −(−3) + 2) o Type mg (Spinning Sidle) perpendicular with the minor
= (1 − 2,3 + 2) - exactly one family of axis of the other family.
= (−1,5)
translations. o Type pgg
Patterns
- Exactly one family of vertical - Exactly 2 families of glide
➢ A collection of one or more families of
reflections reflections
symmetries.
- Exactly one family of half-turn - one family has axis
▪ Rosette Patterns – has unique
(180° rotation) perpendicular with the minor
fixed point
axis of the other family.
o Type cmm Deter No Has Has Has • Includes all non-terminating,
- 2 families of reflections mine Reflec reflect glide both repeating decimals (0.333… and
- 2 families of glide reflections angle tions ions reflect reflect 12.345345345)
o Type pmg of and no only ions ions 5. Irrational Numbers
- One family of reflections Rotati glide only and • Denoted by 𝐐𝟏
- one family of glide reflections on reflect glide • Cntains all numbers that cannot be
- mirror axis perpendicular with ions reflect written as ratio of two integers
the glide axis. ions • Inlcudes all nonterminating
o Type p3m1 360° P1 pm pg cm decimals
- 2 families of reflections 180° P2 pmm pmg Cmm, 6. Real Numbers
- 2 families of glide reflections pmg • Denoted by R
- All 120° rotocenters or 3-fold 120° P3 P3m1, • Contains all rational number
rotocenters lie on the mirror axis p31m • Follows addition, subtraction,
o Type p31m 90° P4 P4m, multiplication and division
- 2 families of reflections p4g 7. Imaginary Numbers
- 2 families of glide reflections 60° P6 P6m
- All 120° rotocenters or 3-fold • Denoted by I
rotocenters don’t lie on the • Contains all numbers of the form
Number Sets
mirror axis 𝑘𝑖 𝑤ℎ𝑒𝑟𝑒 0 ≠ 𝑘𝐸𝑅 𝑎𝑛𝑑 𝑖 2 = −1
1. Natural Numbers or Counting
o Type p4m 8. Complex Numbers
Numbers
- 4 families of reflection • Denoted by C
• Denoted by N
- 2 families of glide reflections • Contains all real numbers and
• Contains 1, 2, 3…
o Type p4g imaginary numbers
• Follows addition and multiplication
- 2 families of reflection • Contains all number of the form 𝑎 +
2. Whole Number
- 4 families of glide reflections 𝑏𝑖, 𝑤ℎ𝑒𝑟𝑒 𝑎, 𝑏𝐸𝑅 𝑎𝑛𝑑 𝑖 2 = −1
Type p6m • Denoted by W
o • A practical term arm of trigonometry
- 120° rotations or 3-fold • Contains 0, 1, 2, 3…
rotocenters • Follows addition and multiplication
- 180° rotations or half-turns 3. Integers C. Fibonacci Sequence and Golden
- 160° rotations or 6-fold rotations • Denoted by Z
Ratio
- 6 families of reflection • Contains 0, 1, -1, 2, -2… Fibonacci Sequence – is the sequence of
- 6 families of glide reflections • Follows addition, subtraction, numbers Fn recursively defined by
multiplication and division
4. Rational Numbers 1
• Denoted by Q 𝐹𝑛 =
𝐹𝑛 − 2 + 𝐹𝑛 − 1
• Contains all numbers of the form Golden Ratios – is denoted by
a/b, where a, b, Z, 𝑏 ≠ 0 Gnomons – consider two figures A and B,
• Follows addition, subtraction, may be necessarily of different size and
multiplication and division shape. B is said to be a gnomon to A if when
• Includes all integers (a=a/1) B is attached to A in a suitable position, the
• Includes all terminating decimals new figure is of the same shape of A.
(0.25 and -12.34567)
Golden Rectangle – consider a square 3. Mathematics helps control
that is gnomon to a rectangle. If the ratio nature and occurrences in
between the length and the width of each the world for our own good;
rectangle is the golden ratio, then each • Health and Epidemic
rectangle is called a golden rectangle. The
square of side p is gnomon of the rectangle • Economics
of length p and width q. Together, they form • Construction Projects
the rectangle of length p+q and width p. • Electromagnetism
Golden Spiral – the union of all quarter- • Population
circles from the previous construction. 4. Mathematics has
Binet’s Formula for Fibonacci applications in many human
Numbers endeavors
• Passion in Literature
• Protecting Biodiversity
• Upgrading Technology
• Management Science
• Space Exploration
Mathematics for our World • Education Research and
Commitment of the Mathematics Assessment
to help the World
1. Mathematics helps organize
patterns and regularities in “ Mathematics is a humble servant of the
the World; people and their problems…and a master
• Time patterns and interpreter of the world and the universe.”
Regularities
• Patterns and Regularities
among life forms
• Physical Patterns and
Regularities
2. Mathematics helps predict
the behavior of nature and
many phenomena
• Weather
• Business and Financial
Trends
• Pregnancy and Fertility
• Human Behavior
You might also like
- Chapter 9 - The Verdict On Groupthink Case StudyDocument2 pagesChapter 9 - The Verdict On Groupthink Case StudyAdelson Arado100% (2)
- Jigsaw AssessmentDocument8 pagesJigsaw AssessmentNur Syafiqah Abu BakarNo ratings yet
- Calculus B: The First Professional IntroductionDocument15 pagesCalculus B: The First Professional IntroductionOgulnabat TashlievaNo ratings yet
- Mathematical Language and Symbols: Math 01 - Mathematics in The Modern WorldDocument30 pagesMathematical Language and Symbols: Math 01 - Mathematics in The Modern WorldMilk BrotherNo ratings yet
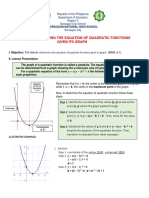
- Determining The Equation of Quadratic Functions Given Its GraphDocument3 pagesDetermining The Equation of Quadratic Functions Given Its GraphElla Jane E. BautistaNo ratings yet
- Nature of MathematicsDocument4 pagesNature of MathematicsAyu PhCareNo ratings yet
- Exam Formula Sheet (1) PhysicsDocument3 pagesExam Formula Sheet (1) PhysicsIncksNo ratings yet
- Grad+Div+Curl Coordinates Part3Document3 pagesGrad+Div+Curl Coordinates Part3christopher23No ratings yet
- On Reduction of Relative Velocity With Relation To Space-Time Co-OrdinateDocument5 pagesOn Reduction of Relative Velocity With Relation To Space-Time Co-OrdinateTathaNo ratings yet
- Mat061 Chapter 2Document40 pagesMat061 Chapter 2Enaira100% (1)
- Partial DerivativesDocument31 pagesPartial DerivativesaliNo ratings yet
- Unit-2 Vector CalculusDocument86 pagesUnit-2 Vector CalculusRitesh MukhNo ratings yet
- PRECALCULUS Quarter 1 Module 3Document6 pagesPRECALCULUS Quarter 1 Module 3alohajilljarabe123No ratings yet
- Math 01 Lecture 2.1Document30 pagesMath 01 Lecture 2.12C1 - YABES, JenniferNo ratings yet
- Module 6 Homogeneous Differential Equation With Constants CoefficientsDocument3 pagesModule 6 Homogeneous Differential Equation With Constants CoefficientsTherese SibayanNo ratings yet
- Learning-Plan-GENERAL MATHEMATICS 11 Lesson 11Document4 pagesLearning-Plan-GENERAL MATHEMATICS 11 Lesson 11Ivy-Jane Natanauan UmandapNo ratings yet
- Tutorial Unit 2Document3 pagesTutorial Unit 2Mukesh KumarNo ratings yet
- BasicCalQ3W2 SLMDocument10 pagesBasicCalQ3W2 SLMNasos 2No ratings yet
- Properties of Complex Numbers (Contd) : NPTEL - Physics - Mathematical Physics - 1Document8 pagesProperties of Complex Numbers (Contd) : NPTEL - Physics - Mathematical Physics - 1vkphyNo ratings yet
- Mathematics 9 Quarter 1 Week 8: NAME: - GR & SEC: - CompetencyDocument11 pagesMathematics 9 Quarter 1 Week 8: NAME: - GR & SEC: - CompetencyPARMAN, REGINE MAYE C.No ratings yet
- M31 Limits Week 1 NotesDocument15 pagesM31 Limits Week 1 NotesYolanda ChangNo ratings yet
- Pre Calculus HandoutsDocument14 pagesPre Calculus HandoutsVince Leo Panoncillon GonzalesNo ratings yet
- Genmathweek 2Document8 pagesGenmathweek 2Ricky LumantaNo ratings yet
- Session 1Document26 pagesSession 1Hao ChenNo ratings yet
- PYL101 QM Lecture 5Document11 pagesPYL101 QM Lecture 5mukeshNo ratings yet
- ME223-Lecture 26 and 27 Thick CylindersDocument19 pagesME223-Lecture 26 and 27 Thick CylindersArushiNo ratings yet
- Null Ticket - Calc-3Document2 pagesNull Ticket - Calc-35gdkrhrjnxNo ratings yet
- Calculus II 2021-2022 S2 MidtermDocument6 pagesCalculus II 2021-2022 S2 MidtermhoqueipatinsportugalNo ratings yet
- Learning-Plan-GENERAL MATHEMATICS 11 Lesson 9 and 10Document4 pagesLearning-Plan-GENERAL MATHEMATICS 11 Lesson 9 and 10Ivy-Jane Natanauan UmandapNo ratings yet
- Chapter 6Document5 pagesChapter 6Muntazir MehdiNo ratings yet
- Questão 01 NOTAÇÃO INDICIALDocument5 pagesQuestão 01 NOTAÇÃO INDICIALAnderson SilvaNo ratings yet
- Chapter 2 Mat455Document36 pagesChapter 2 Mat455Ajaq 98No ratings yet
- Jee Advanced 2022 Paper 2Document13 pagesJee Advanced 2022 Paper 2mickelsonniklaus995No ratings yet
- Lec2 PDFDocument3 pagesLec2 PDFAbhisek RoyNo ratings yet
- Advanced AlgebraDocument10 pagesAdvanced AlgebraMANGULABNAN, REY JOSEPH, E.No ratings yet
- Chapter 1 - Complex NumbersDocument19 pagesChapter 1 - Complex NumbersRyan A. RamosNo ratings yet
- Vector Calculus Add OnDocument86 pagesVector Calculus Add Onabiramijeyaseelan05No ratings yet
- Finite Difference Methods For Two-Point Boundary Value Prob-LemsDocument3 pagesFinite Difference Methods For Two-Point Boundary Value Prob-LemsasasdNo ratings yet
- Lecture-5-6 Moment, Skewness and KurtosisDocument5 pagesLecture-5-6 Moment, Skewness and KurtosisNafiul Alam SnigdhoNo ratings yet
- Unit 1 - Topic 2Document24 pagesUnit 1 - Topic 2lorenzjohn777No ratings yet
- Class 10 Math Formulas (C.B.S.E)Document6 pagesClass 10 Math Formulas (C.B.S.E)Vaibhav RachapudiNo ratings yet
- Analytic Geometry (11-21)Document4 pagesAnalytic Geometry (11-21)blueberrytimeNo ratings yet
- Quadratic Functions: B. Learning Outcome Performance StandardDocument7 pagesQuadratic Functions: B. Learning Outcome Performance StandardHenry Kahal Orio Jr.No ratings yet
- Notes Zeghib1Document15 pagesNotes Zeghib1JordandomNo ratings yet
- Calculus Module 3Document22 pagesCalculus Module 3Karl AngcananNo ratings yet
- LIVE NOTES DIFFERENTIAL CALCULUS FOR SL Students of AA and AIDocument26 pagesLIVE NOTES DIFFERENTIAL CALCULUS FOR SL Students of AA and AIsriramaniyerNo ratings yet
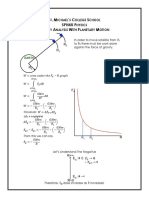
- Sph4u Note Energy Analysis + Planetary MotionDocument3 pagesSph4u Note Energy Analysis + Planetary MotionDavid HilbergNo ratings yet
- 1 2 J P Total 1 2 I X P Total: Estimation of One Missing Observation in LSDDocument3 pages1 2 J P Total 1 2 I X P Total: Estimation of One Missing Observation in LSDSerajum Monira MouriNo ratings yet
- 3a. Plane Stress - Plane Strain 2 StuDocument36 pages3a. Plane Stress - Plane Strain 2 Stushivam ojhaNo ratings yet
- Solution Manual Chapter 7Document14 pagesSolution Manual Chapter 7Hazlina ZaiyunanNo ratings yet
- NSEP 2022 Question Paper With SolutionsDocument46 pagesNSEP 2022 Question Paper With SolutionsATRIJA PALNo ratings yet
- Calculus II 2018-2019 S2 Midterm Test 2Document3 pagesCalculus II 2018-2019 S2 Midterm Test 2Frank WanNo ratings yet
- IT5409 - Ch6-Motion Detection and Tracking-Eng v1.0Document58 pagesIT5409 - Ch6-Motion Detection and Tracking-Eng v1.0Bui Minh DucNo ratings yet
- Formula Sheet PhysicsDocument2 pagesFormula Sheet PhysicsThar Lon Lin HtetNo ratings yet
- BYJU'S Home Learning Program: Daily Practice ProblemsDocument5 pagesBYJU'S Home Learning Program: Daily Practice ProblemsJagdamba prasad yadavNo ratings yet
- Module in General Mathematics: OBJECTIVE: Determines The Intercepts, Zeroes, and Asymptotes of An Exponential FunctionDocument20 pagesModule in General Mathematics: OBJECTIVE: Determines The Intercepts, Zeroes, and Asymptotes of An Exponential FunctionMarco SeəsonNo ratings yet
- 1st DLP-MATHEMATICS8-OCTOBER 20, 2023Document5 pages1st DLP-MATHEMATICS8-OCTOBER 20, 2023karlajean bongatoNo ratings yet
- SC Grade 9 Unit 5 - MensurationDocument21 pagesSC Grade 9 Unit 5 - MensurationJitender sehrawatNo ratings yet
- Math IA On CalculusDocument9 pagesMath IA On CalculusZehraNo ratings yet
- Application of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsFrom EverandApplication of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- Inverse Trigonometric Functions (Trigonometry) Mathematics Question BankFrom EverandInverse Trigonometric Functions (Trigonometry) Mathematics Question BankNo ratings yet
- Applications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankFrom EverandApplications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankNo ratings yet
- Navigating Digital Ethiopia A Look Into EthiopiaDocument4 pagesNavigating Digital Ethiopia A Look Into Ethiopiabekyab53No ratings yet
- Binary Lesson WorksheetsDocument8 pagesBinary Lesson WorksheetsmyschoolonthegoNo ratings yet
- Tense: Atle Grønn and Arnim Von StechowDocument29 pagesTense: Atle Grønn and Arnim Von StechowCamila SilvestreNo ratings yet
- Forklift Vocabulary 2Document2 pagesForklift Vocabulary 2Alexandra KogukharNo ratings yet
- The Bug Shop: Ben Nagy & The GrugqDocument47 pagesThe Bug Shop: Ben Nagy & The Grugqtimtom123No ratings yet
- Spatial Variation in Evapotranspiration and The Influence of Land Use On Catchment HydrologyDocument25 pagesSpatial Variation in Evapotranspiration and The Influence of Land Use On Catchment HydrologyDaniel PabonNo ratings yet
- Quiz CworldDocument1 pageQuiz Cworldforda ytpremiumNo ratings yet
- Detail Drawing of Pump and Blower Room ITBPDocument1 pageDetail Drawing of Pump and Blower Room ITBPAminur RahmanNo ratings yet
- Instant Download Mri in Practice 4th Edition Ebook PDF PDF FREEDocument15 pagesInstant Download Mri in Practice 4th Edition Ebook PDF PDF FREEronald.dancy562100% (52)
- Sustainable Energy, Grids and NetworksDocument8 pagesSustainable Energy, Grids and NetworksРоман БуйнийNo ratings yet
- Mental Health & Wellbeing For Children & Young People - Part TwoDocument24 pagesMental Health & Wellbeing For Children & Young People - Part Twomariya khanNo ratings yet
- Chapter 3: Fundamentals of CrystallographyDocument51 pagesChapter 3: Fundamentals of CrystallographyAli ZbayelNo ratings yet
- The Role of Public Relations in Organiza Tional Crisis ManagementDocument2 pagesThe Role of Public Relations in Organiza Tional Crisis ManagementSalahudeen GbolahanNo ratings yet
- Chapter 1 MergedDocument65 pagesChapter 1 MergedAdi SaputraNo ratings yet
- The Impact of Desktop Publishing and Secretaries Performance ReviewedDocument11 pagesThe Impact of Desktop Publishing and Secretaries Performance ReviewedwaheedbasitadebayoNo ratings yet
- Alpha RT PDFDocument8 pagesAlpha RT PDFHugo GranadosNo ratings yet
- Airbus 29 A300 A310 HydraulicsDocument186 pagesAirbus 29 A300 A310 HydraulicsElijah Paul Merto86% (7)
- Data Sheet Ulf 600 Pro2Document3 pagesData Sheet Ulf 600 Pro2Salman ZaheerNo ratings yet
- Multi-Stage Reciprocating CompressorsDocument14 pagesMulti-Stage Reciprocating CompressorsSajad FalahNo ratings yet
- Grade 5 - Arts ActivitiesDocument7 pagesGrade 5 - Arts ActivitiesMarcus Sayson DabonNo ratings yet
- LogDocument6 pagesLogDaniel SousaNo ratings yet
- The 7 Laws of Clearing Ca Final 9350712539Document83 pagesThe 7 Laws of Clearing Ca Final 9350712539sanjay sNo ratings yet
- Good Things Come To Those Who Wait, But Only Those Things Left by Those Who Hustle' by Abraham LincolnDocument12 pagesGood Things Come To Those Who Wait, But Only Those Things Left by Those Who Hustle' by Abraham Lincolnsiva_mmNo ratings yet
- Cek Virus CMDDocument3 pagesCek Virus CMDMohamad Razif Abd RazakNo ratings yet
- RoberDocument2 pagesRoberVernet LactNo ratings yet
- Resilient Marketing Ebook FDocument20 pagesResilient Marketing Ebook Fmaneesh mittalNo ratings yet
- Baeng 102Document7 pagesBaeng 102Chinni ChinniNo ratings yet
- Acp Module 2.1Document36 pagesAcp Module 2.1Ashly Sacdalan ViolandaNo ratings yet