Professional Documents
Culture Documents
Lect08 Greedy K Center
Lect08 Greedy K Center
Uploaded by
Anthony-Dimitri ACopyright:
Available Formats
You might also like
- Cheat SheetDocument4 pagesCheat SheetjelmoodNo ratings yet
- Solu 8Document35 pagesSolu 8Alisen ErdoganNo ratings yet
- Additional Exercises For Convex OptimizationDocument116 pagesAdditional Exercises For Convex OptimizationQuoc Viet PhamNo ratings yet
- Factoring Polynomials: A Presentation For The Greatest Algebra I Kids at RJRDocument25 pagesFactoring Polynomials: A Presentation For The Greatest Algebra I Kids at RJRBoqorka America100% (1)
- Least Squares Fitting of Spatial CirclesDocument31 pagesLeast Squares Fitting of Spatial CirclesthimbuNo ratings yet
- Scribe Week4Document3 pagesScribe Week4EdwardNo ratings yet
- Kmeans Is Np-HardDocument15 pagesKmeans Is Np-Hardshraddha212No ratings yet
- Dosang Joe and Hyungju Park: Nal Varieties. Rational Parametrizations of The Irreducible ComponentsDocument12 pagesDosang Joe and Hyungju Park: Nal Varieties. Rational Parametrizations of The Irreducible ComponentsMohammad Mofeez AlamNo ratings yet
- Modular Arithmetic: Clocks and CirclesDocument3 pagesModular Arithmetic: Clocks and CirclesSaleh MuhammedNo ratings yet
- Improved Conic Reformulations For K-Means Clustering: Madhushini Narayana Prasad and Grani A. HanasusantoDocument24 pagesImproved Conic Reformulations For K-Means Clustering: Madhushini Narayana Prasad and Grani A. HanasusantoNo12n533No ratings yet
- Closest Pairs ClusteringDocument4 pagesClosest Pairs ClusteringMATAMALA13No ratings yet
- Estimating The Support of A High-Dimensional DistributionDocument28 pagesEstimating The Support of A High-Dimensional DistributionAndrés López GibsonNo ratings yet
- New Algorithms For K-Center and Extensions: Abstract. The Problem of Interest Is Covering A Given Point Set WithDocument15 pagesNew Algorithms For K-Center and Extensions: Abstract. The Problem of Interest Is Covering A Given Point Set WithsanjibNo ratings yet
- Effective Construction of Convex Hull AlgorithmsDocument8 pagesEffective Construction of Convex Hull AlgorithmsKasun Ranga WijeweeraNo ratings yet
- Ada Module 3 NotesDocument40 pagesAda Module 3 NotesLokko PrinceNo ratings yet
- Lattin Et Al - Analyzing Multivariate Data - 279-281Document3 pagesLattin Et Al - Analyzing Multivariate Data - 279-281vigneshNo ratings yet
- Daa Unit 3Document22 pagesDaa Unit 3Rahul GusainNo ratings yet
- Lab 08 SolutionsDocument5 pagesLab 08 Solutionsdawit gebreyohansNo ratings yet
- K-Means++: The Advantages of Careful Seeding: David Arthur and Sergei VassilvitskiiDocument11 pagesK-Means++: The Advantages of Careful Seeding: David Arthur and Sergei VassilvitskiiAhmad Luky RamdaniNo ratings yet
- 1 Hw6 SolutionsDocument8 pages1 Hw6 SolutionsdavejaiNo ratings yet
- 19 Leiden SupDocument14 pages19 Leiden SupAndi MunteanuNo ratings yet
- ACM ICPC Finals 2012 SolutionsDocument5 pagesACM ICPC Finals 2012 Solutionsbarunbasak1No ratings yet
- Fusion Trees ReportDocument6 pagesFusion Trees ReportViren shaNo ratings yet
- BV Cvxbook Extra ExercisesDocument156 pagesBV Cvxbook Extra ExercisesAnonymous WkbmWCa8MNo ratings yet
- Extra Exercises PDFDocument232 pagesExtra Exercises PDFShy PeachDNo ratings yet
- Straightedge CompassDocument26 pagesStraightedge CompassSamuel SilvaNo ratings yet
- Additional Exercises For Convex Optimization: Stephen Boyd Lieven Vandenberghe March 30, 2012Document143 pagesAdditional Exercises For Convex Optimization: Stephen Boyd Lieven Vandenberghe March 30, 2012api-127299018No ratings yet
- BVCvxbook Extra ExercisesDocument192 pagesBVCvxbook Extra ExercisesThe DudeNo ratings yet
- BV Cvxbook Extra ExercisesDocument139 pagesBV Cvxbook Extra ExercisesAkhil AmritaNo ratings yet
- Rec2 SolDocument6 pagesRec2 Solm22ai569No ratings yet
- Aditional Exercises Boyd PDFDocument164 pagesAditional Exercises Boyd PDFlandinluklaNo ratings yet
- 2017 CSN523 T1 Solution PDFDocument3 pages2017 CSN523 T1 Solution PDFsaiavinash duddupudiNo ratings yet
- Numerical Conformal Mapping Using Cross-Ratios and Delaunay TriangulationDocument21 pagesNumerical Conformal Mapping Using Cross-Ratios and Delaunay TriangulationkevinalmerNo ratings yet
- Problem Set 2: InstructionsDocument4 pagesProblem Set 2: InstructionsballechaseNo ratings yet
- Solu 8Document35 pagesSolu 8Basil Aziz TinahNo ratings yet
- Nahp1 2020 PDFDocument4 pagesNahp1 2020 PDFVangheli TVNo ratings yet
- Computational Geometry Practice Final - Solution NotesDocument4 pagesComputational Geometry Practice Final - Solution NotesBibodiNo ratings yet
- BV Cvxbook Extra Exercises PDFDocument152 pagesBV Cvxbook Extra Exercises PDFSoumitra BhowmickNo ratings yet
- Roch Mmids Intro 3clusteringDocument15 pagesRoch Mmids Intro 3clusteringaslamzohaibNo ratings yet
- Design and AnalysisDocument5 pagesDesign and Analysisflame1406No ratings yet
- Assign 7Document5 pagesAssign 7KEERTHANA KNo ratings yet
- Problem: Late Homework Policy. Cooperation PolicyDocument13 pagesProblem: Late Homework Policy. Cooperation PolicyMath Homework SolverNo ratings yet
- Chapter 7Document11 pagesChapter 7Dandu Kalyan VarmaNo ratings yet
- Approx AlgoDocument70 pagesApprox AlgoNikhil VermaNo ratings yet
- Handbook of Cluster Analysis: C. Hennig, M. Meila, F. Murtagh, R. Rocci (Eds.)Document28 pagesHandbook of Cluster Analysis: C. Hennig, M. Meila, F. Murtagh, R. Rocci (Eds.)Andreas DamanikNo ratings yet
- MCMC OriginalDocument6 pagesMCMC OriginalAleksey OrlovNo ratings yet
- BV Cvxbook Extra ExercisesDocument117 pagesBV Cvxbook Extra ExercisesAsif AhmedNo ratings yet
- BÀI TẬP GT LỒIDocument127 pagesBÀI TẬP GT LỒIkhongtinNo ratings yet
- Additional Exercises For Convex Optimization PDFDocument187 pagesAdditional Exercises For Convex Optimization PDFCliffordTorresNo ratings yet
- Lecture3 - Convex Sets and Convex FunctionsDocument9 pagesLecture3 - Convex Sets and Convex Functionsanon_245742684No ratings yet
- Thi Giac May Tinh - Vo Quang Hoang Khang - Ex6 (Cuuduongthancong - Com)Document3 pagesThi Giac May Tinh - Vo Quang Hoang Khang - Ex6 (Cuuduongthancong - Com)Tiến Anh NguyễnNo ratings yet
- W9a Autoencoders PcaDocument7 pagesW9a Autoencoders PcazeliawillscumbergNo ratings yet
- Approximation Algorithms 1Document56 pagesApproximation Algorithms 1sandhiyasubramaniyan2001No ratings yet
- iαb iαa π 2Document3 pagesiαb iαa π 2monu991No ratings yet
- Final 13Document9 pagesFinal 13نورالدين بوجناحNo ratings yet
- Grouped Outlier Removal For Robust Ellipse FittingDocument4 pagesGrouped Outlier Removal For Robust Ellipse FittingAbhra BasakNo ratings yet
- HW02 - KNN DTDocument3 pagesHW02 - KNN DTghukasyans033No ratings yet
- The K-Centrum Multi-Facility Location Problem: Arie TamirDocument15 pagesThe K-Centrum Multi-Facility Location Problem: Arie TamirJoyNo ratings yet
- 10-601 Machine Learning: Homework 7: InstructionsDocument5 pages10-601 Machine Learning: Homework 7: InstructionsSasanka Sekhar SahuNo ratings yet
- BV Cvxbook Extra ExercisesDocument237 pagesBV Cvxbook Extra ExercisesWilian GuamánNo ratings yet
- Lect14 Flow DefsDocument4 pagesLect14 Flow DefsAnthony-Dimitri ANo ratings yet
- Cours8 HandoutDocument72 pagesCours8 HandoutAnthony-Dimitri ANo ratings yet
- Notes On x86-64 ProgrammingDocument7 pagesNotes On x86-64 ProgrammingAnthony-Dimitri ANo ratings yet
- Lect15 Flow Ford FulkDocument6 pagesLect15 Flow Ford FulkAnthony-Dimitri ANo ratings yet
- Mount 451 2017Document202 pagesMount 451 2017Anthony-Dimitri ANo ratings yet
- Lect20 NP 3satDocument6 pagesLect20 NP 3satAnthony-Dimitri ANo ratings yet
- Lect18 NP DefsDocument5 pagesLect18 NP DefsAnthony-Dimitri ANo ratings yet
- CMSC 451: Lecture 13 All-Pairs Shortest Paths and The Floyd-Warshall AlgorithmDocument5 pagesCMSC 451: Lecture 13 All-Pairs Shortest Paths and The Floyd-Warshall AlgorithmAnthony-Dimitri ANo ratings yet
- CMSC 451: Lecture 16 Network Flow Algorithms: Thursday, Nov 7, 2016Document7 pagesCMSC 451: Lecture 16 Network Flow Algorithms: Thursday, Nov 7, 2016Anthony-Dimitri ANo ratings yet
- Lect17 Flow CircDocument8 pagesLect17 Flow CircAnthony-Dimitri ANo ratings yet
- Lect07 Greedy SchedDocument9 pagesLect07 Greedy SchedAnthony-Dimitri ANo ratings yet
- Lect21 NP Clique VC DsDocument6 pagesLect21 NP Clique VC DsAnthony-Dimitri ANo ratings yet
- Lect06 Greedy HuffmanDocument7 pagesLect06 Greedy HuffmanAnthony-Dimitri ANo ratings yet
- Lect19 NP ReducDocument6 pagesLect19 NP ReducAnthony-Dimitri ANo ratings yet
- Lect02 Graph BasicsDocument7 pagesLect02 Graph BasicsAnthony-Dimitri ANo ratings yet
- cmsc754 2020 01 HandoutsDocument32 pagescmsc754 2020 01 HandoutsAnthony-Dimitri ANo ratings yet
- Lect Exf RevDocument3 pagesLect Exf RevAnthony-Dimitri ANo ratings yet
- cmsc451 2015 08 HandoutsDocument34 pagescmsc451 2015 08 HandoutsAnthony-Dimitri ANo ratings yet
- cmsc754 Spring2020 LectsDocument221 pagescmsc754 Spring2020 LectsAnthony-Dimitri ANo ratings yet
- cmsc451 Fall15 LectsDocument197 pagescmsc451 Fall15 LectsAnthony-Dimitri ANo ratings yet
- Lect05 Graph Shortest PathDocument7 pagesLect05 Graph Shortest PathAnthony-Dimitri ANo ratings yet
- CMSC 451: Lecture 1 Introduction To Algorithm Design: Tuesday, Aug 29, 2017Document4 pagesCMSC 451: Lecture 1 Introduction To Algorithm Design: Tuesday, Aug 29, 2017Anthony-Dimitri ANo ratings yet
- CMSC 251: Algorithms: Spring 1998Document30 pagesCMSC 251: Algorithms: Spring 1998Anthony-Dimitri ANo ratings yet
- cmsc420 2020 08 HandoutsDocument53 pagescmsc420 2020 08 HandoutsAnthony-Dimitri ANo ratings yet
- cmsc420 Fall2020 LectsDocument156 pagescmsc420 Fall2020 LectsAnthony-Dimitri ANo ratings yet
- IntegersDocument3 pagesIntegersRonalyn LimNo ratings yet
- Taylor SeriesDocument6 pagesTaylor SeriesJunior Briones VelizNo ratings yet
- Sheet-2 (Vector Space) - 1Document4 pagesSheet-2 (Vector Space) - 1Soumadeep PatraNo ratings yet
- Nota Pembezaan 1Document38 pagesNota Pembezaan 1Syaa MalyqaNo ratings yet
- Topic 7 - Optimisation - Simplex MethodDocument48 pagesTopic 7 - Optimisation - Simplex Methodwongh ka manNo ratings yet
- Solution1 VaDocument4 pagesSolution1 VamarshadjaferNo ratings yet
- Simulation and Modelimg of Turbulent Flows - Lumley J.L.Document329 pagesSimulation and Modelimg of Turbulent Flows - Lumley J.L.vsammartanoNo ratings yet
- Kernel Methods!: Sargur Srihari!Document29 pagesKernel Methods!: Sargur Srihari!asdfasdffdsaNo ratings yet
- Math g8 m2 Topic B Lesson 10 Teacher PDFDocument11 pagesMath g8 m2 Topic B Lesson 10 Teacher PDFSujatha VimalNo ratings yet
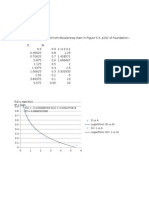
- Boussinesq Plot & Equation For PilesDocument24 pagesBoussinesq Plot & Equation For PilesJoshua GibbingsNo ratings yet
- Chapter 2Document50 pagesChapter 2iffahNo ratings yet
- Assignment 4 Geometric TransformationsDocument2 pagesAssignment 4 Geometric TransformationsKrish100% (1)
- Tic Tac Toe Review Chapter 5Document19 pagesTic Tac Toe Review Chapter 5api-313709590No ratings yet
- Differential Equation Part 2Document25 pagesDifferential Equation Part 2ABHRANEEL KARMAKARNo ratings yet
- Group and Ring MTH312Document151 pagesGroup and Ring MTH312Dejene GirmaNo ratings yet
- Mathematics Mock BoardDocument2 pagesMathematics Mock BoardArabella SanchezNo ratings yet
- 2.1 Locating Roots: Chapter Two Non Linear EquationsDocument13 pages2.1 Locating Roots: Chapter Two Non Linear EquationsAbel MediaNo ratings yet
- Deriving Using Product and Quotient Rules: Michael Turner Alex BarboloviciDocument31 pagesDeriving Using Product and Quotient Rules: Michael Turner Alex BarboloviciAlex BarboloviciNo ratings yet
- GATE Control Systems by KanodiaDocument97 pagesGATE Control Systems by Kanodiakaran11364% (11)
- 7 1eDocument29 pages7 1eSyed Nabeel Ali100% (1)
- KMM Geilo 2012 Lecture 10Document42 pagesKMM Geilo 2012 Lecture 10islaNo ratings yet
- NM3 Root s02Document15 pagesNM3 Root s02sori1386No ratings yet
- An Economic Dispatch Algorithm For Cogeneration Systems: M. A. Gonzalez Chapa, and J. R. Vega GalazDocument6 pagesAn Economic Dispatch Algorithm For Cogeneration Systems: M. A. Gonzalez Chapa, and J. R. Vega Galazsebaa haddiNo ratings yet
- MATH1030 CH 9Document16 pagesMATH1030 CH 9Shaikh Hassan AtikNo ratings yet
- Examen Unidad 1 y 2 Carlos Manuel Perez BibianoDocument14 pagesExamen Unidad 1 y 2 Carlos Manuel Perez Bibianojennifer guzmanNo ratings yet
- Argand Diagrams and The Polar FormDocument12 pagesArgand Diagrams and The Polar FormHassaan650No ratings yet
- 1 LPPDocument18 pages1 LPPpks009No ratings yet
Lect08 Greedy K Center
Lect08 Greedy K Center
Uploaded by
Anthony-Dimitri AOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Lect08 Greedy K Center
Lect08 Greedy K Center
Uploaded by
Anthony-Dimitri ACopyright:
Available Formats
CMSC 451 Dave Mount
CMSC 451: Lecture 8
Greedy Approximation Algorithms: The k-Center Problem
Tuesday, Sep 26, 2017
Reading: A variant of this problem is dicussed in Chapt 11 in KT and Section 9.2.2 in DPV.
Greedy Approximation for NP-Hard Problems: One of the common applications of greedy
algorithms is for producing approximation solutions to NP-hard problems.
As we shall see later this semester, NP-hard optimization problems represent very challenging
computational problems in the sense that there is no known exact solution that has worst-case
polynomial-time running time. Given an NP-hard problem, there are no ideal algorithmic
solutions. One has to compromise between optimality or running time. Nonetheless, there
are are number of examples of NP-hard problems where simple greedy heuristics produce
solutions that are not far from optimal.
Clustering and Center-Based Clustering: Clustering is a widely studied problem with appli-
cations in statistics, pattern recognition, and machine learning. In a nutshell, it involves
partition a large set of objects, called points, into a small number of subsets whose members
are all mutually close to one another. In machine learning, clustering is often performed in
high-dimensional spaces. Each data object is associated with a property vector, a numeric
vector whose length may range from tens to thousands that describes the salient properties
of this object. Then clustering is performed to group similar objects together.
In this geometric view of clustering, we think of the data set as a set P of n points in a
multi-dimensional space (see Fig. 1(a)). The output of the clustering algorithm is the set
C = {c1 , . . . , ck } of points called cluster centers or simply centers (see Fig. 1(b)). Depending
on the method being employed, it may be required that the center points are drawn from P
itself, or they may just be arbitrary points in space, sometimes called Steiner points. In our
example, the cluster centers have been chosen from P .
P c2 c8
c4
c7
c3 c9
c1 c5
N (c5)
c6
(a) (b) (c)
Fig. 1: Center-based geometry clustering.
Given a center point ci , the associated cluster are the points of P that are closer to ci center
than to any other cluster center. We refer to this as ci ’s neighborhood, denoted N (ci ). In
Fig. 1(c), we show a subdivision of space into nine regions according to which cluster center is
closest, and highlight the neighborhood N (c5 ) in particular. (By the way, this subdivision is a
famous structure in geometry, called the Voronoi diagram of the cluster centers. Computing
Lecture 8 1 Fall 2017
CMSC 451 Dave Mount
Voronoi diagrams is covered in a course on Computational Geometry, but it is not necessary
for our purposes. In O(nk) time we can compute the distance between each of the n points
and each of the k centers, and assign each point to its closest center.)
The k-Center Problem: There are many ways in which to define clustering as an optimization
problem. We will consider one of the simplest. We are given a set P of n points in space. For
each pair of points u, v ∈ P , let δ(u, v) denote the distance between u and v. We will assume
that the distance satisfies the typical properties of any natural distance function:
Positivity: δ(u, v) ≥ 0 and δ(u, v) = 0 if and only if u = v.
Symmetry: δ(u, v) = δ(v, u)
Triangle inequality: δ(u, w) ≤ δ(u, v) + δ(v, w)
For the rest of the lecture, we can think of δ as the Euclidean distance, but the algorithm
that we will present can be applied to any function satisfying the above properties.
k-center problem: Given a set P of n points in space and an integer k ≤ n, find a set
C ⊆ P of k points in order to minimize the maximum distance of any point of P to its
closest center in C.
Why maximum distance and not, say, sum of distances? There are many formulations of
clustering, and this is the one that we have chosen for now.
We can view the k-center problem as a covering problem by balls. Given a point x in space
and radius r, define the ball B(x, r) to be the (closed) ball of radius r centered at x. Given
any solution C to the k-center problem, let ∆(C) denote the maximum distance from any
point of P to its closest center. If we now place balls of radius ∆(C) about each point in C,
it is easy to see that every point of P lies within the union of these balls. By definition of
∆(C), one of the points of P will lie on the boundary of one of these balls (for otherwise we
could make ∆(C) smaller). The neighborhood of each cluster will lie within its associated
ball (see Fig. 2(b)).
Input: k=6 c4 ∆(C)
c2
c3 c6
c1 c5
(a) (b)
Fig. 2: The k-center problem in the Euclidean plane.
Given this perspective, we can see that the k-center problem is equivalent to the following
problem:
k-center problem (equivalent form): Given a set P of n points in space and an integer
k ≤ n, find the minimum radius ∆ and a set of balls of radius ∆ centered at k points of
P such that P lies within the union of these balls.
Lecture 8 2 Fall 2017
CMSC 451 Dave Mount
Greedy Approximation Algorithm: Like many clustering problems, the k-center problem is
known to be NP-hard, and so we will not be able to solve it exactly. (We will show this
later this semester for a graph-based variant of the k-center problem.) Today, we will present
a simple greedy algorithm that does not produce the optimum value of ∆, but only an
approximation to its value. Our algorithm will produce an estimate that is at most twice as
large as the optimum value of ∆.
Let us start with a couple of useful definitions. Given a set C = {c1 , . . . , ck } of centers and
for any ci ∈ C, define the bottleneck distance of ci to be the distance to its farthest point in
N (ci ), that is,
∆(ci ) = max δ(v, ci ).
v∈N (ci )
Clearly, the maximum bottleneck distance over all the centers is just ∆(C).
Intuitively, if we think of the cluster centers as the locations of Starbucks (or your favorite
retailer), then each customer (point in P ) is associated with the closest Starbucks. The set
N (ci ) are the customers that go to the ith Starbucks location, and ∆(ci ) is the maximum
distance any of these customers needs to travel to get to ci . ∆(C) is the maximum distance
that anyone needs to travel to their nearest Starbucks.
The greedy algorithm begins by selecting any point of P to be the initial center g1 . We
then repeat the following process until we have k centers. Let Gi = {g1 , . . . , gi } denote the
current set of centers. Recall that ∆(Gi ) is the maximum distance of any point of P from
its nearest center. Let u be the point achieving this distance. Intuitively, u is the most
dissatisfied customer, since he/she has to drive the farthest to get to the nearest Starbucks.
The greediest way to satisfy u is to put the next center directly at u. (Thus plopping the
next Starbucks right on top of u’s house. Are you satisfied now?) In other words, set
gi+1 ← u and Gi+1 ← Gi ∪ {gi+1 }.
The pseudocode is presented in the code block below. The value d[u] denotes the distance
from u to its closest center. (We make one simplification, by starting with G being empty.
When we select the first center, all the points of P have infinite distances, so the initial choice
is arbitrary.)
It is easy to see that the algorithm’s running time is O(kn). In general k ≤ n, so this is O(n2 )
in the worst case. One step of the algorithm is illustrated in Fig. 3. Assuming that we have
three centers G = {g1 , g2 , g3 }, let g4 be the point that is farthest from its nearest center (g1
in this case). In each step we create a center at g4 , so now G = {g1 , . . . , g4 }. In anticipation
of the next step, we find the point that maximizes the distance to its closest center (g5 in this
case), and if the algorithm continues, it will be the location of the next center.
Approximation Bound: Now, let us show that this algorithm is at most a factor of 2 from the
optimum. Let G = {g1 , . . . , gk } denote the set of centers computed by the greedy algorithm,
and let ∆(G) denote its bottleneck distance. Let O = {o1 , . . . , ok } denote the optimum set
of centers, that is the set of k centers such that ∆(O) is the smallest possible. We will show
that greedy is at most twice as bad as optimal, that is,
∆(G) ≤ 2∆(O).
Lecture 8 3 Fall 2017
CMSC 451 Dave Mount
Greedy Approximation for k-center
GreedyKCenter(P, k) {
G = empty
for each u in P do // initialize distances
d[u] = INFINITY
for (i = 1 to k) {
Let u be the point of P such that d[u] is maximum
Add u to G // u is the next cluster center
for (each v in P) { // update distance to nearest center
d[v] = min(d[v], distance(v,u))
}
Delta = max_{v in P} d[v] // update the bottleneck distance
}
return (G, Delta) // final centers and max distance
}
g4 g4
∆3
g1
g1
g5
∆4
g3 g3
g2 g2
Fig. 3: Greedy approximation to k-center (from stage 3 to 4).
Lecture 8 4 Fall 2017
CMSC 451 Dave Mount
Of course, we don’t know what O is or even what ∆(O) is. Our approach will be to determine
a lower bound ∆min on the optimum bottleneck distance (∆min ≤ ∆(O)). We will then
show that our algorithm produces a value that is at most twice this lower bound value
(∆(G) ≤ 2∆min ). It will follow therefore that ∆(G) ≤ 2∆(O).
The analysis is based on the following three claims, each of which is quite straightforward
to prove. Define Gi to be the set of greedy centers after the ith execution of the algorithm,
and let ∆i = ∆(Gi ) denote its overall bottleneck distance (the fartest any point is from its
closest center in Gi . The greedy algorithm stops with gk , but for the sake of the analysis it is
convenient to consider the next center to be added if we ran it for one more iteration. That
is, define gk+1 to be the point of P that is maximizes the distance to its closest center in Gk .
(This distance is ∆(Gk ).) Also, define Gk+1 = {g1 , . . . , gk+1 }.
Claim 1: For 1 ≤ i ≤ k + 1, ∆i+1 ≤ ∆i . That is, the sequence of bottleneck distances is
monotonically nonincreasing. (In Fig. 3 this is represented by the fact that the radii of
the covering disks decrease with each stage.)
Proof: Whenever we add a new center, the distance to each point’s closest center will either
be the same or will decrease. Therefore, the maximum of such a set can never increase.
Claim 2: For 1 ≤ i ≤ k + 1, every pair of greedy centers in Gi is separated by a distance of
at least ∆i−1 .
Proof: Consider the ith stage. By the induction hypothesis, the first i − 1 centers are
separated from each other by distance ∆i−2 ≥ ∆i−1 . The ith center is, by definition, at
distance ∆i−1 from its closest center, and therefore it is at distance at least ∆i−1 from
all the other centers.
Claim 3: Let ∆min = ∆(G)/2. Then for any set C of k cluster centers, ∆(C) ≥ ∆min .
Proof: By definition of ∆(C) we know that every point of P lies within distance ∆(C) of
some point of C, and since G ⊆ P , this is true for G as well. Since |Gk+1 | = k + 1, by
the pigeonhole principle, there exists at least two centers g, g 0 ∈ Gk+1 that are in the
same neighborhood of some center c ∈ C, that is, max(δ(g, c), δ(g 0 , c)) ≤ ∆(c). Since
g, g 0 ∈ Gk+1 , by Claim 2, δ(g, g 0 ) ≥ ∆k = ∆(G). By applying the triangle inequality to
the triple (g, c, g 0 ) and symmetry of the distance function, we have
∆(G) ≤ δ(g, g 0 ) ≤ δ(g, c) + δ(c, g 0 ) (by triangle inequality)
0
≤ δ(g, c) + δ(g , c) (by distance symmetry)
≤ ∆(c) + ∆(c) ≤ ∆(C) + ∆(C) = 2∆(C).
Therefore, ∆(C) ≥ ∆(G)/2 = ∆min , as desired.
Now, by applying Claim 3 to O, we have ∆(O) ≥ ∆min . By definition, ∆min = ∆(G)/2, and
so ∆(G) ≤ 2∆(O), completing the analysis.
You might wonder whether this bound is tight. We will leave it as an exercise to prove that
there is a input such that (if you are unlucky about how you choose the first point) the greedy
algorithm returns a value that is arbitrarily close to twice that of the optimum.
Lecture 8 5 Fall 2017
You might also like
- Cheat SheetDocument4 pagesCheat SheetjelmoodNo ratings yet
- Solu 8Document35 pagesSolu 8Alisen ErdoganNo ratings yet
- Additional Exercises For Convex OptimizationDocument116 pagesAdditional Exercises For Convex OptimizationQuoc Viet PhamNo ratings yet
- Factoring Polynomials: A Presentation For The Greatest Algebra I Kids at RJRDocument25 pagesFactoring Polynomials: A Presentation For The Greatest Algebra I Kids at RJRBoqorka America100% (1)
- Least Squares Fitting of Spatial CirclesDocument31 pagesLeast Squares Fitting of Spatial CirclesthimbuNo ratings yet
- Scribe Week4Document3 pagesScribe Week4EdwardNo ratings yet
- Kmeans Is Np-HardDocument15 pagesKmeans Is Np-Hardshraddha212No ratings yet
- Dosang Joe and Hyungju Park: Nal Varieties. Rational Parametrizations of The Irreducible ComponentsDocument12 pagesDosang Joe and Hyungju Park: Nal Varieties. Rational Parametrizations of The Irreducible ComponentsMohammad Mofeez AlamNo ratings yet
- Modular Arithmetic: Clocks and CirclesDocument3 pagesModular Arithmetic: Clocks and CirclesSaleh MuhammedNo ratings yet
- Improved Conic Reformulations For K-Means Clustering: Madhushini Narayana Prasad and Grani A. HanasusantoDocument24 pagesImproved Conic Reformulations For K-Means Clustering: Madhushini Narayana Prasad and Grani A. HanasusantoNo12n533No ratings yet
- Closest Pairs ClusteringDocument4 pagesClosest Pairs ClusteringMATAMALA13No ratings yet
- Estimating The Support of A High-Dimensional DistributionDocument28 pagesEstimating The Support of A High-Dimensional DistributionAndrés López GibsonNo ratings yet
- New Algorithms For K-Center and Extensions: Abstract. The Problem of Interest Is Covering A Given Point Set WithDocument15 pagesNew Algorithms For K-Center and Extensions: Abstract. The Problem of Interest Is Covering A Given Point Set WithsanjibNo ratings yet
- Effective Construction of Convex Hull AlgorithmsDocument8 pagesEffective Construction of Convex Hull AlgorithmsKasun Ranga WijeweeraNo ratings yet
- Ada Module 3 NotesDocument40 pagesAda Module 3 NotesLokko PrinceNo ratings yet
- Lattin Et Al - Analyzing Multivariate Data - 279-281Document3 pagesLattin Et Al - Analyzing Multivariate Data - 279-281vigneshNo ratings yet
- Daa Unit 3Document22 pagesDaa Unit 3Rahul GusainNo ratings yet
- Lab 08 SolutionsDocument5 pagesLab 08 Solutionsdawit gebreyohansNo ratings yet
- K-Means++: The Advantages of Careful Seeding: David Arthur and Sergei VassilvitskiiDocument11 pagesK-Means++: The Advantages of Careful Seeding: David Arthur and Sergei VassilvitskiiAhmad Luky RamdaniNo ratings yet
- 1 Hw6 SolutionsDocument8 pages1 Hw6 SolutionsdavejaiNo ratings yet
- 19 Leiden SupDocument14 pages19 Leiden SupAndi MunteanuNo ratings yet
- ACM ICPC Finals 2012 SolutionsDocument5 pagesACM ICPC Finals 2012 Solutionsbarunbasak1No ratings yet
- Fusion Trees ReportDocument6 pagesFusion Trees ReportViren shaNo ratings yet
- BV Cvxbook Extra ExercisesDocument156 pagesBV Cvxbook Extra ExercisesAnonymous WkbmWCa8MNo ratings yet
- Extra Exercises PDFDocument232 pagesExtra Exercises PDFShy PeachDNo ratings yet
- Straightedge CompassDocument26 pagesStraightedge CompassSamuel SilvaNo ratings yet
- Additional Exercises For Convex Optimization: Stephen Boyd Lieven Vandenberghe March 30, 2012Document143 pagesAdditional Exercises For Convex Optimization: Stephen Boyd Lieven Vandenberghe March 30, 2012api-127299018No ratings yet
- BVCvxbook Extra ExercisesDocument192 pagesBVCvxbook Extra ExercisesThe DudeNo ratings yet
- BV Cvxbook Extra ExercisesDocument139 pagesBV Cvxbook Extra ExercisesAkhil AmritaNo ratings yet
- Rec2 SolDocument6 pagesRec2 Solm22ai569No ratings yet
- Aditional Exercises Boyd PDFDocument164 pagesAditional Exercises Boyd PDFlandinluklaNo ratings yet
- 2017 CSN523 T1 Solution PDFDocument3 pages2017 CSN523 T1 Solution PDFsaiavinash duddupudiNo ratings yet
- Numerical Conformal Mapping Using Cross-Ratios and Delaunay TriangulationDocument21 pagesNumerical Conformal Mapping Using Cross-Ratios and Delaunay TriangulationkevinalmerNo ratings yet
- Problem Set 2: InstructionsDocument4 pagesProblem Set 2: InstructionsballechaseNo ratings yet
- Solu 8Document35 pagesSolu 8Basil Aziz TinahNo ratings yet
- Nahp1 2020 PDFDocument4 pagesNahp1 2020 PDFVangheli TVNo ratings yet
- Computational Geometry Practice Final - Solution NotesDocument4 pagesComputational Geometry Practice Final - Solution NotesBibodiNo ratings yet
- BV Cvxbook Extra Exercises PDFDocument152 pagesBV Cvxbook Extra Exercises PDFSoumitra BhowmickNo ratings yet
- Roch Mmids Intro 3clusteringDocument15 pagesRoch Mmids Intro 3clusteringaslamzohaibNo ratings yet
- Design and AnalysisDocument5 pagesDesign and Analysisflame1406No ratings yet
- Assign 7Document5 pagesAssign 7KEERTHANA KNo ratings yet
- Problem: Late Homework Policy. Cooperation PolicyDocument13 pagesProblem: Late Homework Policy. Cooperation PolicyMath Homework SolverNo ratings yet
- Chapter 7Document11 pagesChapter 7Dandu Kalyan VarmaNo ratings yet
- Approx AlgoDocument70 pagesApprox AlgoNikhil VermaNo ratings yet
- Handbook of Cluster Analysis: C. Hennig, M. Meila, F. Murtagh, R. Rocci (Eds.)Document28 pagesHandbook of Cluster Analysis: C. Hennig, M. Meila, F. Murtagh, R. Rocci (Eds.)Andreas DamanikNo ratings yet
- MCMC OriginalDocument6 pagesMCMC OriginalAleksey OrlovNo ratings yet
- BV Cvxbook Extra ExercisesDocument117 pagesBV Cvxbook Extra ExercisesAsif AhmedNo ratings yet
- BÀI TẬP GT LỒIDocument127 pagesBÀI TẬP GT LỒIkhongtinNo ratings yet
- Additional Exercises For Convex Optimization PDFDocument187 pagesAdditional Exercises For Convex Optimization PDFCliffordTorresNo ratings yet
- Lecture3 - Convex Sets and Convex FunctionsDocument9 pagesLecture3 - Convex Sets and Convex Functionsanon_245742684No ratings yet
- Thi Giac May Tinh - Vo Quang Hoang Khang - Ex6 (Cuuduongthancong - Com)Document3 pagesThi Giac May Tinh - Vo Quang Hoang Khang - Ex6 (Cuuduongthancong - Com)Tiến Anh NguyễnNo ratings yet
- W9a Autoencoders PcaDocument7 pagesW9a Autoencoders PcazeliawillscumbergNo ratings yet
- Approximation Algorithms 1Document56 pagesApproximation Algorithms 1sandhiyasubramaniyan2001No ratings yet
- iαb iαa π 2Document3 pagesiαb iαa π 2monu991No ratings yet
- Final 13Document9 pagesFinal 13نورالدين بوجناحNo ratings yet
- Grouped Outlier Removal For Robust Ellipse FittingDocument4 pagesGrouped Outlier Removal For Robust Ellipse FittingAbhra BasakNo ratings yet
- HW02 - KNN DTDocument3 pagesHW02 - KNN DTghukasyans033No ratings yet
- The K-Centrum Multi-Facility Location Problem: Arie TamirDocument15 pagesThe K-Centrum Multi-Facility Location Problem: Arie TamirJoyNo ratings yet
- 10-601 Machine Learning: Homework 7: InstructionsDocument5 pages10-601 Machine Learning: Homework 7: InstructionsSasanka Sekhar SahuNo ratings yet
- BV Cvxbook Extra ExercisesDocument237 pagesBV Cvxbook Extra ExercisesWilian GuamánNo ratings yet
- Lect14 Flow DefsDocument4 pagesLect14 Flow DefsAnthony-Dimitri ANo ratings yet
- Cours8 HandoutDocument72 pagesCours8 HandoutAnthony-Dimitri ANo ratings yet
- Notes On x86-64 ProgrammingDocument7 pagesNotes On x86-64 ProgrammingAnthony-Dimitri ANo ratings yet
- Lect15 Flow Ford FulkDocument6 pagesLect15 Flow Ford FulkAnthony-Dimitri ANo ratings yet
- Mount 451 2017Document202 pagesMount 451 2017Anthony-Dimitri ANo ratings yet
- Lect20 NP 3satDocument6 pagesLect20 NP 3satAnthony-Dimitri ANo ratings yet
- Lect18 NP DefsDocument5 pagesLect18 NP DefsAnthony-Dimitri ANo ratings yet
- CMSC 451: Lecture 13 All-Pairs Shortest Paths and The Floyd-Warshall AlgorithmDocument5 pagesCMSC 451: Lecture 13 All-Pairs Shortest Paths and The Floyd-Warshall AlgorithmAnthony-Dimitri ANo ratings yet
- CMSC 451: Lecture 16 Network Flow Algorithms: Thursday, Nov 7, 2016Document7 pagesCMSC 451: Lecture 16 Network Flow Algorithms: Thursday, Nov 7, 2016Anthony-Dimitri ANo ratings yet
- Lect17 Flow CircDocument8 pagesLect17 Flow CircAnthony-Dimitri ANo ratings yet
- Lect07 Greedy SchedDocument9 pagesLect07 Greedy SchedAnthony-Dimitri ANo ratings yet
- Lect21 NP Clique VC DsDocument6 pagesLect21 NP Clique VC DsAnthony-Dimitri ANo ratings yet
- Lect06 Greedy HuffmanDocument7 pagesLect06 Greedy HuffmanAnthony-Dimitri ANo ratings yet
- Lect19 NP ReducDocument6 pagesLect19 NP ReducAnthony-Dimitri ANo ratings yet
- Lect02 Graph BasicsDocument7 pagesLect02 Graph BasicsAnthony-Dimitri ANo ratings yet
- cmsc754 2020 01 HandoutsDocument32 pagescmsc754 2020 01 HandoutsAnthony-Dimitri ANo ratings yet
- Lect Exf RevDocument3 pagesLect Exf RevAnthony-Dimitri ANo ratings yet
- cmsc451 2015 08 HandoutsDocument34 pagescmsc451 2015 08 HandoutsAnthony-Dimitri ANo ratings yet
- cmsc754 Spring2020 LectsDocument221 pagescmsc754 Spring2020 LectsAnthony-Dimitri ANo ratings yet
- cmsc451 Fall15 LectsDocument197 pagescmsc451 Fall15 LectsAnthony-Dimitri ANo ratings yet
- Lect05 Graph Shortest PathDocument7 pagesLect05 Graph Shortest PathAnthony-Dimitri ANo ratings yet
- CMSC 451: Lecture 1 Introduction To Algorithm Design: Tuesday, Aug 29, 2017Document4 pagesCMSC 451: Lecture 1 Introduction To Algorithm Design: Tuesday, Aug 29, 2017Anthony-Dimitri ANo ratings yet
- CMSC 251: Algorithms: Spring 1998Document30 pagesCMSC 251: Algorithms: Spring 1998Anthony-Dimitri ANo ratings yet
- cmsc420 2020 08 HandoutsDocument53 pagescmsc420 2020 08 HandoutsAnthony-Dimitri ANo ratings yet
- cmsc420 Fall2020 LectsDocument156 pagescmsc420 Fall2020 LectsAnthony-Dimitri ANo ratings yet
- IntegersDocument3 pagesIntegersRonalyn LimNo ratings yet
- Taylor SeriesDocument6 pagesTaylor SeriesJunior Briones VelizNo ratings yet
- Sheet-2 (Vector Space) - 1Document4 pagesSheet-2 (Vector Space) - 1Soumadeep PatraNo ratings yet
- Nota Pembezaan 1Document38 pagesNota Pembezaan 1Syaa MalyqaNo ratings yet
- Topic 7 - Optimisation - Simplex MethodDocument48 pagesTopic 7 - Optimisation - Simplex Methodwongh ka manNo ratings yet
- Solution1 VaDocument4 pagesSolution1 VamarshadjaferNo ratings yet
- Simulation and Modelimg of Turbulent Flows - Lumley J.L.Document329 pagesSimulation and Modelimg of Turbulent Flows - Lumley J.L.vsammartanoNo ratings yet
- Kernel Methods!: Sargur Srihari!Document29 pagesKernel Methods!: Sargur Srihari!asdfasdffdsaNo ratings yet
- Math g8 m2 Topic B Lesson 10 Teacher PDFDocument11 pagesMath g8 m2 Topic B Lesson 10 Teacher PDFSujatha VimalNo ratings yet
- Boussinesq Plot & Equation For PilesDocument24 pagesBoussinesq Plot & Equation For PilesJoshua GibbingsNo ratings yet
- Chapter 2Document50 pagesChapter 2iffahNo ratings yet
- Assignment 4 Geometric TransformationsDocument2 pagesAssignment 4 Geometric TransformationsKrish100% (1)
- Tic Tac Toe Review Chapter 5Document19 pagesTic Tac Toe Review Chapter 5api-313709590No ratings yet
- Differential Equation Part 2Document25 pagesDifferential Equation Part 2ABHRANEEL KARMAKARNo ratings yet
- Group and Ring MTH312Document151 pagesGroup and Ring MTH312Dejene GirmaNo ratings yet
- Mathematics Mock BoardDocument2 pagesMathematics Mock BoardArabella SanchezNo ratings yet
- 2.1 Locating Roots: Chapter Two Non Linear EquationsDocument13 pages2.1 Locating Roots: Chapter Two Non Linear EquationsAbel MediaNo ratings yet
- Deriving Using Product and Quotient Rules: Michael Turner Alex BarboloviciDocument31 pagesDeriving Using Product and Quotient Rules: Michael Turner Alex BarboloviciAlex BarboloviciNo ratings yet
- GATE Control Systems by KanodiaDocument97 pagesGATE Control Systems by Kanodiakaran11364% (11)
- 7 1eDocument29 pages7 1eSyed Nabeel Ali100% (1)
- KMM Geilo 2012 Lecture 10Document42 pagesKMM Geilo 2012 Lecture 10islaNo ratings yet
- NM3 Root s02Document15 pagesNM3 Root s02sori1386No ratings yet
- An Economic Dispatch Algorithm For Cogeneration Systems: M. A. Gonzalez Chapa, and J. R. Vega GalazDocument6 pagesAn Economic Dispatch Algorithm For Cogeneration Systems: M. A. Gonzalez Chapa, and J. R. Vega Galazsebaa haddiNo ratings yet
- MATH1030 CH 9Document16 pagesMATH1030 CH 9Shaikh Hassan AtikNo ratings yet
- Examen Unidad 1 y 2 Carlos Manuel Perez BibianoDocument14 pagesExamen Unidad 1 y 2 Carlos Manuel Perez Bibianojennifer guzmanNo ratings yet
- Argand Diagrams and The Polar FormDocument12 pagesArgand Diagrams and The Polar FormHassaan650No ratings yet
- 1 LPPDocument18 pages1 LPPpks009No ratings yet