Chapter 12 • Limits and Continuity

______
(a) Is f (x) = √ x2 – 25 continuous in the______
open interval (–10, –5)?
Let c  (–10, –5), then xlim
→c
f (x) = √ c2 – 25 = f (c) for all c between
–10 and –5. Hence, the first condition is satisfied.
(b) Does lim + f (x) = f (–10)?
x → –10 ______ ___
We have lim + f (x) = lim + √ x2 – 25 = √ 75 = f (–10). Hence, the
x → –10 x → –10
second condition is satisfied.
(c) Does lim – f (x) = f (–5)?
x → –5 ______
We have lim – f (x) = lim – √ x2 – 25 = 0 = f (5). Hence, the third
x → –5 x → –5
condition is satisfied.
______
Hence, we conclude that f (x) = √ x2 – 25 is continuous in the closed
interval [–10, –5].

Exercise 12.5
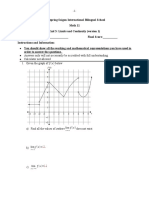
1. Determine whether the following functions are continuous at the given points.
(a) f (x) = 2x_____
3
– 5, at x = 2
(b) f (x) = √ x – 3 , at x = 4
2

x–2
(c) f (x) = _____
x – 3 , at x = 3
x2, x < 3
(d) f (x) = , at x = 3
1 – x 2, x  3
x2 – 1, x  1
(e) f (x) = , at x = 1
1 – x, x < 1
x + 2, x  –1
(f) f (x) = x2, –1 < x < 1 , at x = –1 and 1
0, x  1

2. Given that f (x) = |x + 2|, sketch the graph and discuss the continuity of the function.

x2 + k, x < 1
3. Given that f (x) = is continuous in the interval (–∞, ∞), find k.
x3, x  1

4. A function f is defined as follows:

1, x  –1
f (x) = 1 – kx, –1 < x < 1
(x –1), x  1
(a) Given that f is continuous at x = 1, find the value of constant k.
(b) Determine whether f is continuous at x = –1.
(c) Sketch the graph of y = f (x).

379

Pre-Calculus and Calculus.indb 379 13/7/2017 5:57:30 PM

 Chapter 12 • Limits and Continuity

5. A function is defined as follows:

4x + 1
______
f (x) = x–2 ,x<2
3x + 2, x  2
5
Determine whether f is continuous at x = __
3.
______
6. (a) Sketch the graph of f (x) = √ 3x – x2 and determine the continuity of f in the interval [0, 3].
______
√ 3x – x2
_______
(b) State the set of values of x such that f (x) = x + 2 is not continuous.

_____
7. (a) Sketch the graph of f (x) = √ x2 – 9 and state the interval where f is continuous.
(b) Function g is defined as follows:
x – k,
2
_____ –3 < x < 3
g (x) =
√ x – 9 , others
2

Given that g is continuous for all values of x, find k.

8. Function f is defined as follows:

ex, x  0
f (x) =
1 – 4x2, x < 0
(a) Find lim f (x).
x→0
(b) Determine whether f is continuous at x = 0. Explain your answer.
(c) Sketch the graph of y = f (x) for –2  x  2.

9. (a) State the conditions for a function f to be continuous at x = a.

(b) A function f is defined as follows:
x2 – 4
______
, x≠2
f (x) = x – 2
3, x = 2
(i) Sketch the graph.
(ii) Discuss the continuity of f at x = 2.

10. A function g is defined as follows:

x, x < –2
g(x) = px + q, –2  x  2
x
__
2 – 1, x > 2
Determine the values of the constants p and q such that g is continuous in the interval (–∞, ∞).

380

Pre-Calculus and Calculus.indb 380 13/7/2017 5:57:30 PM