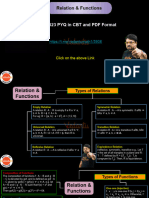
Mind map : learning made simple Chapter - 1

The composition of functions f : A → B A relation R : A → A is empty

}
and g : B → C is denoted by gof, and is if a R b ∀ a, b∈ A. R = φ ⊂ A ×A.
defined as gof : A → C given by gof(x) = For eg : R = {(a,b) : a = b2}, A = {1,5,10}
Trivial
g(f(x)) ∀x∈A. e.g. let A = N and f, g :
A relation R : A → A is universal Relations
N → N such that f(x) = x2 and g(x) = x3
if a R b ∀, a,b ∈ A,R = A × A.
∀ x∈N. Then gof(2) = g(f(2)) = g(2 ) 2

3
if R = φ, then R is universal.
= 4 = 64.
A relation R : A → A is
A function f : x → y is invertible, if ∃ a function reflexive if aRa ∀ a∈A
g : y → x such that gof = Ix and fog = Iy. Then,
g is the inverse of f. If f is invertible, then it is both +
one-one and onto and vice-versa. For eg. If f(x) = A relation R : A → A is symmetric
x and f : N → N , then f is invertible. if aRb ⇒ bRa ∀ a, b∈A
Theorem 1 : If f : x → y, g : y → z and h : z → s +
are functions, then ho(got) = (hog)of. A relation R : A × A is transitive
Theorem 2 : Let f : x → y and g : y → z be two if aRb, bRc ⇒ aRc ∀ a,b,c ∈A.
invertible functions, then gof is invertible and
–1 –1 –1
Relations
(gof) = f o g . and Functions
Equivalence relation
(reflexive, symmetric, transitive e.g.,
Let T = the set of all triangles in a
plane and R : T → T defined by
R = {(T1, T2)} : T1 is congruent to T2}.
A binary operation '*' on a set A is a function Then, R is equivalence.
* : A × A → A denoted by a * b i.e. ∀
a,b,∈ A, a * b ∈ A. Commutative if a * b = b f : x → y is one-one if f : x → y is onto it for energy f : x → y is both one-one
* a ∀ a,b ∈ A. Associative if (a * b) * c = a f(x1) = f(x2) ⇒ x1 = x2 y ∈ Y, ∃ x∈X S.t. f(x) = y, f2 is onto. and onto, then f is bijective.
* (b * c) ∀a,b,∈A. e∈A is identity if a * e = a ∀ x1, x2 ∈ x. Other wise, f3 is bijective.
= e * a ∀a∈A. and b ∈ A is the inverse f is many- one, f1 is one-one.
of a ∈ A, if. a * b = e = b * a. Addition is a f1 f2 f3
1 a a 1 a
binary operation on the set of integers. b
1
2
2 2 b
cd 3 b 3 c
3